城市蔓延机理与治理：经济与制度视角

2　城模市型空及间其增应长用 的理论

1960年代之后，随着以Alonso的投标租金理论为代表的静态城市经济模型的兴起，基于城市经济学的视角研究城市空间增长成为西方城市空间问题研究的热点之一，也极大地扩展和深化了对该问题的研究。

2．1　城市空间增长经济模型的演进

20世纪60年代以来，以竞租模型为基础的西方城市经济理论取得重大突破，为研究城市土地利用以及空间增长提供了很好的视角（顾杰，2006）。

2．1．1　杜能农业区位论

竞租模型是城市经济学诞生的基础，其直接理论来源可以追溯到德国经济学家杜能开创的农业区位论。杜能是19世纪德国著名的农业经济学家，他在长期经营农场经验的基础上，采用孤立抽象的研究方法，提出了著名的农业圈层理论，也就是农业区位论，最早阐述了农业生产布局规律。

为了便于研究，杜能首先将复杂的地理环境假设为一个简单的“孤立国”。这些假设包括：①孤立国是一片匀质平原，并孤立于世界之外，四周为荒地所包围。在孤立国中央是唯一的大城市，城市是这一区域剩余产品的唯一市场。城市的周围是其农业腹地，负责向城市提供农产品。②孤立国的腹地是匀质的，即有相同的土壤肥力、气候等地理环境，也就是具有完全相同的发展农业的自然条件。③孤立国内交通条件完全相同，区内唯一的交通工具是能穿行于农田间的马车，且运费同运输距离及重量成正比。④孤立国内的农业经营者的经营条件和经营技能完全相同，且以追求最大利润为目的，孤立国内农产品价格、劳动者工资和利息率固定不变。

从这些假设条件出发，杜能认为某一地方种植何种作物最为有利完全取决于利润（P），而利润是农产品市场价格（V）与其成本（E）和运费（T）的差额。三者的关系可以用式（2－1）来表示：

上述等式通过移项可以写成P＋T＝V－E。由于杜能已经假设在一定时期内农产品的价格是固定不变的，而且孤立国内发展农业的条件是完全一样，因此各地生产同一产品的成本也是固定的。这样一来，等式的右边就为一个常数，也就是说利润和运费之和是一个常数。因此，只有把运费开支压缩到最小才能得到最大利润。这样杜能的农业布局理论就转化为如何合理地布局农业来节约运费，从而最大限度地增加利润。

杜能将他所观察到的数据带入式（2－1）中，计算出各种农作物合理的种植界限，得到孤立国中不同农业经营类型将围绕城市呈同心圆环状分布（图2－1）。

图2－1　杜能模型中的城市同心圆环状结构

杜能将空间概念引入经济问题研究，解释了区位级差地租与城市空间结构的关系，为城市经济学的研究奠定了基础。到了1960年代，Alonso在杜能模型的基础上，提出了经典的竞租模型，开创了城市经济学研究的先河。

2．1．2　城市经济静态模型

Alonso（1964）、Muth（1969）、Mills（1972）和Brueckner（1983）在杜能模型的基础上，建立了竞租模型（The Bid－Rent Model）和单中心城市一般均衡分析框架，也就是城市经济静态模型。

Alonso的竞租模型假设城市是一个没有任何特征的平原，区位用到市中心的距离来表示，家庭对区位和消费束的选择由一个静态效用最大化模型来描述。Alonso通过一系列的假设指出，各种用地需求竞争不同区位的土地，最后在城市土地市场均衡时形成了城市土地利用结构。由于不同的预算约束，各个土地使用者对于同一区位的经济评估（单位面积土地的投入和产出）是不一致的；并且，随着与城市中心距离的递增（意味着区位可达性的递减），各种土地使用者的效益递减速率（边际效益的变化）也是不相同的。基于这样的假设，Alonso提出的核心概念是不同土地使用者的竞租曲线（Bid－Rent Curves），其表示土地成本和区位成本（克服空间距离的交通成本）之间的权衡，类似于新古典主义经济学的无差别曲线（Indifference Curves）。不同的曲线表示不同的土地使用方式，曲线上的任何一点表示一种选址可能性；同一曲线上任何一种选择方案的经济效益（土地成本和区位成本之和）都是相同的。于是，城市土地使用的空间分布模式就可以用一组地租竞价曲线来加以表示（图2－2）。

Alosno是在一个家庭直接消费土地的框架中进行的研究，此后，Muth（1969）和Mills（1967，1972）进一步发展了Alonso的单一城市中心模型，在效用函数中以住房替代了土地，建立了一个更真实的模型。Muth和Evans在Wingo－Alonso城市经济模型的基础上发展了住房选择的“互换论（Trade off Model）”，认为城市居民通过对住房成本（即购或租一定区位的住房的费用）与通勤费用的权衡来确定合适的住宅区位。在均衡时，住房价格（租金）随着距市中心的距离增大而降低。该模型预测，当城市处于均衡状态时，土地（住房）的价值或租金在有更多城市人口的城市里更高；在有更高交通成本和更低收入的城市里，地租函数的斜率更陡峭。

以Alonso的理论为主的新古典城市地租理论，成功地将空间关系和距离因素引进经济学领域中。在Krugman看来，这个框架是所有经济地理研究中最接近标准新古典主流的理论（Krugman，1995）。但该理

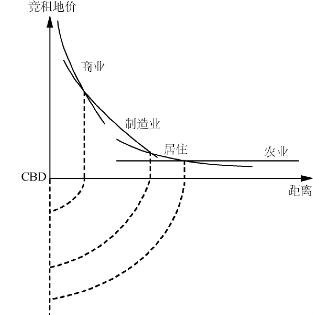
图2－2　Alonso模型中的城市土地使用空间分布模式

论的致命弱点就是，建立模型的前提是假定城市是静态的，预言不了城市兴起和多中心城市结构的出现。因此，该理论在后来受到诸多质疑，最主要的质疑即是其将住房及城市空间视为均质性的假设、单中心的假设以及对城市的静态分析。

2．1．3　城市经济动态模型

城市经济静态模型（单一的城市中心模型）预测和推断出土地价格和土地利用强度、人口密度随距离的增加而降低。然而，在城市经济动态模型里，城市增长是一个渐进过程，土地利用密度取决于城市土地开发时的经济状况。土地利用密度并不一定随距离的增加而降低，其也可以随距离的增加而增加。因为，随着时间推移，经济状况会发生变化，如收入增加和通勤费用降低等，因此土地租金或价格、人口密度会随通勤费用的降低而增加。这一结论同城市经济静态理论正好截然不同。此外，城市经济静态理论模型指出，土地价格与地租成正比，在城市边缘地带城市土地地租等于农业土地地租。然而，在城市动态模型里，这两个结论都不成立（丁成日，2002）。因此，有很多城市经济学家将研究的重点转到城市发展中的城市地租和土地价值变化以及由此导致的需求和供给的变动。

Capozza ＆Helsley（1989）在一个简单的城市经济动态模型中分析了城市增长中土地价格的基本构成。在资本具有耐久性以及土地所有者对未来有完全地预见性的假设条件下，城市内的土地价格有四个不可分的组成部分：①农业土地价值；②当前的位置价格，即可达性的经济价值；③土地开发成本；④可预见的未来位置价值增长，也称城市增长土地价值溢价（Growth Premium）。城市边缘之外的土地价格，由两部分组成：①农用地价值；②可预见的土地转变成城市用地后未来土地地租增值所带来的价值。由于这种增长要在未来的开发时间才能获得，所以其值以指数形式下降。对于更外围的地方，由于开发将是很久乃至遥遥无期的事情，预期租金增长的现值接近于零，土地价格仅仅是农用地价值。

Capozza ＆Helsley（1989）认为，随着市场条件的变化，土地价格的各组成部分也会发生变化。如果城市没有增长，而且预期也不会增长，那么城市增长土地价值溢价变为零。若城市预期有增长时，则预期的开发使城市外围的空置土地有了价值。这种预期导致的价格上升不仅表现为城市外围空置土地价格的上升，还表现为城市内部已开发区域的住宅价格或土地价格的上升。

他们还认为，城市增长土地价值溢价是城市发展（人口和经济）引起的。城市发展越快，土地地租增值的也越快，城市增长土地价值溢价也就越高，城市增长土地价值溢价占土地价值的比重越大。反之，如果城市增长速度很慢，甚至不增长，土地地租增值就会很小，甚至是零，城市增长土地价值溢价在土地价值的比重可以忽略不计。他们还指出，在快速增长的城市中，增长溢价可以占到土地平均价格的一半，并且使城市边缘的土地价格（减去开发成本）和农业地租的价值之间有很大的差距。据估计，如果城市人口增长速度为2%的话，城市增长土地价值溢价占土地价值的27%；如果城市人口增长速度为4%，城市增长土地价值溢价占土地价值的59%。显然，城市增长土地价值溢价是城市土地价值的主要组成部分（Mills，1994）。

Dispasquale ＆Wheaton（1996）在Capozza ＆Helsley的动态研究思路下，构造了一个更为真实的模型。在他们的模型中，住房是一种最终消费品，而土地是住房生产过程重点的中间投入。他们根据补偿租金（李嘉图租金，Ricardian Rent）理论分析了城市增长过程中的住房租金和价格的组成。他们指出，当增长率发生变化时，市场会调整对未来增长的预期，由此造成城市土地或住房价格的剧烈变化（尽管即期租金可能保持稳定）。他们认为，房地产价格的变动大部分原因来源于对未来租金收益增长预测的变化，而不是当前租金的实际变化。在其他条件不变时，预期增长速度快的城市会有较低的资本化率；而城市内，城市边缘相对于市中心，租金增长较快，资本化率相对较低。当城市边缘随着时间变化扩张时，城市内部的资本化率将会上升。

虽然，Capozza ＆Helsley以及Dispasquale ＆Wheaton在分析思路上存在一定的差异，但二者的结论是一致的，都揭示了城市增长预期对土地价值的影响，这为研究快速城市化进程中的城市空间增长提供了很好的理论框架。城市经济动态理论及其结论丰富和发展了城市土地、住房价值理论，加深了对土地或住房价值形成和发展的理解。城市经济动态模型为我们分析城市空间增长以及城市土地价格变化提供了很好的视角。

2．2　基于竞租理论的城市空间增长分析

接下来，我们以竞租理论为基础，分别用城市经济的静态模型和动态模型来分析城市空间增长的过程以及驱动城市空间增长的主要因素。

2．2．1　基于静态模型的分析

为了分析的便利，我们提出以下假设：（1）该区域坐落于均质平原上，由城市和农村组成，其中城市位于区域中央，并且被农村包围；（2）城市集中了所有的非农经济活动，而农村仅进行农业生产；（3）商业中心（CBD）位于城市的中央，所有的就业机会都集中在CBD，而城市居民住在CBD的外围，需要通勤到CBD；（4）交通网络是均质分布，城市居民从居住地到CBD的总交通费用就只决定于从住所到市中心的距离；（5）所有城市居民具有相同的收入、消费倾向和效用函数。除了以上的假设之外，竞租模型还有几个隐含的既定：所有土地都掌握在一个所有者手中，而且对于不同的土地使用者不存在歧视，市场是完全竞争的，农用地的产出为零等。

假设城市土地在不同家庭之间进行分配。家庭通过住宅区位的选择，实现效用最大化。假设效用函数用v（C，L）表示，L表示家庭住宅占据的土地面积，C表示除住宅之外的复合商品，城市居民通过选择最优的消费组合（C，L）来使满意度（Utility Level）最大化（效用函数最优化），即：

考虑到家庭的效用水平要受到预算的约束。假设城市居民住宅到CBD的距离为x，居民可支配收入为Y，单位通勤成本为k，单位土地租金水平为r。假定复合商品的价格为1，于是预算约束条件为：

由式（2－3）可以得到：

将式（2－4）代入式（2－2），得：

式（2－5）的优化问题简化为对L求极值的问题，其必要条件为：

整理后可以得到：

接下来以x为参变量对式（2－5）进行全微分，得：

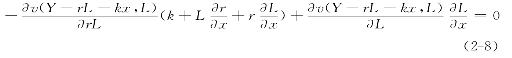
将式（2－7）代入式（2－8）可以得到：

式（2－9）说明，随着到城市中心区（CBD）距离的增大，土地租金水平下降。土地价格的空间递减规律说明，靠近城市中心的居民比远离城市中心的居民的交通成本小。为了保证城市居民的满意度空间不变，靠近城市中心的居民要支付比远离城市中心的居民高的土地价格。城市居民要在两项中作出抉择：一是高交通成本，低土地价格（城市郊区）；二是低交通成本，高土地价格（市中心）（丁成日，2008）。

接下来我们来分析土地所有者的行为。土地所有者的目标函数是将土地收益（租金收入）最大化。为了简化分析，假定土地开发的（资本）密度不随时间变化，换句话说，单位土地开发强度是固定的。根据城市经济学的相关模型，其目标函数定义为：

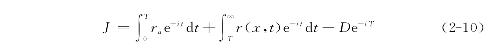
公式（2－10）中，r（x，t）代表城市土地地租；ra代表非城市土地地租；T代表土地开发的时间；i代表折现率（Discount Rate）；D代表土地开发总成本；x代表区位；t代表时间。T是决策变量，即某块未开发的土地的未来开发时间，也就是说，在时间T，非城市土地开发成城市土地。公式（2－10）右边的第一项代表土地开发前的总土地收益，第二项代表土地开发后的总土地收益，第三项代表土地开发成本。所有的土地收益和开发成本都折成当前的价值以便比较。

公式（2－10）最大值的必要条件是：

于是可以得到：

式（2－12）说明当城市土地地租（r（T，x，k））等于农业土地地租（ra）加上土地开发成本（iD），土地将从农业用地转变为城市用地，从而城市实现空间扩展。其中，iD表示银行贷款成本——假设土地开发成本全部来自银行贷款（假设土地有所者从银行贷款总额为D，利息率等于折旧率）。k为常数时，将从地租函数中消失。在统一的市场机制下，城市的边界为城市土地地租等于农业土地地租加上土地开发成本的点上。

图2－3中，A表示城市土地地租曲线，B表示城市土地地租曲线A平移后的位置。根据式（2－10）可以得出最优土地开发时间T的隐函数为T（x）＝T（r（T，k），ra，i，D）。该函数具有特性：，意味着土地价格的上升将推动土地开发（使土地开发时间提前）；，意味着交通成本的降低（如高速公路的建设）将推动土地开发；0，意味着农业土地租金的上升将推迟土地开发；，意味着土地开发成本的上升将推迟土地开发。

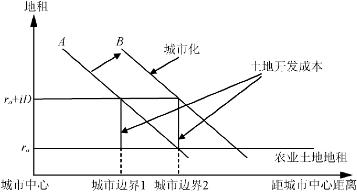
图2－3　最佳开发时机时的城市边界

在此基础上，丁成日界定了两种不同的城市向外进行空间扩展的动力机制（图2－4）（丁成日，2005）：一是由于城市化和收入的增加导致城市土地地租曲线向外平移；另一个是在城市总人口不变的情况下，由于交通的发展（如高速公路的建设）使城市土地地租曲线逆时针地旋转。前者是城市化带来的空间外延，后者是城市郊区化带来的空间外延。

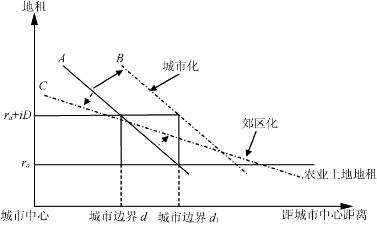
图2－4　简化的城市空间扩展示意图

2．2．2　基于动态模型的分析

1）Capozza＆Helsley模型

假设效用函数极均质（Homogeneous of Degree 1），即：于是有：

由式（2－3）可以得到：

假设在城市边缘进行土地开发，式（2－12）说明城市边缘在时间t的土地地租为：

假设v（t）为随时间变化的城市居民效用函数值，于是有：

公式（2－15）中隐含土地租金函数关系为：

公式（2－17）意味着城市土地租金由3个部分组成：农业土地租金；土地开发成本租金；区位或可达性所带来的级差地租（Location or Accessibility Rent）。当区位超出城市边界时（x＞X（t）），土地租金等于农业土地租金，即：

已开发城市土地在区位x的土地价值为（Pd（t，x））为：

其中，t1表示土地开发的时间，将式（2－17）代入式（2－19），得：

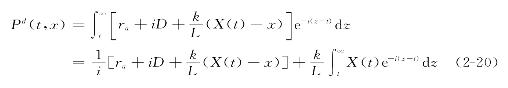
对公式（2－20）右边最后一项部分积分，得：

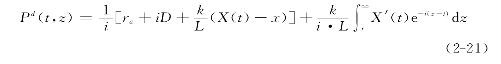
其等价于（根据公式（2－17））：

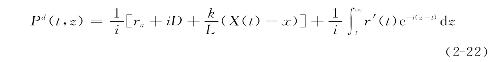
在这一模型中，已开发土地的价格被分解为4个部分：农业土地价值（A／r）；土地开发成本C；可达性的经济价值（（1／i）（k／L）［X（t）－x］）；可预见的未来土地租金增值所带来的价值（（1／i）·，其也称为城市增长的土地价值溢价，即这部分土地价值是由于城市发展（人口和经济）而产生的。城市发展速度越快，土地租金增值也就越快，进而城市增长土地价值溢价也就越高，城市增长土地价值溢价占土地价值的比重越大。反之，如果城市增长速度很慢，甚至不增长，土地租金增长就会很小，甚至为零（城市人口通常总是不断增加，故仅在极个别情况下城市才会衰退，进而走向死亡，城市内部分地区的衰退不在此列），这时，城市土地租金的主要构成是农业土地价值、土地开发成本、可达性的经济价值。城市增长土地溢价所占的比重可以忽略不计。(www.xing528.com)

通过类似的方法，我们可以得到农业土地的价格。

如果区位x的土地在时间t还没有被开发成城市用地，则其价值为：

将公式（2－17）代入公式（2－23），得到：

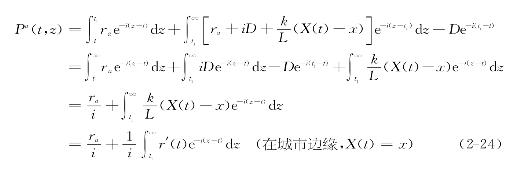
公式（2－24）显示城市边缘农业土地价值由两部分构成：资本化的土地租金；可预见的农业土地转变为城市用地后，土地租金增值所带来的

价值

上述分析可以总结为两张简单的图。图2－5表示城市边界内、外的租金。城市边界之外是农业土地租金。在城市边缘，由于有将生地转变为熟地的机会成本，租金发生跳跃。在城市边界内部，租金以单位土地单位距离的交通成本的比率增加。

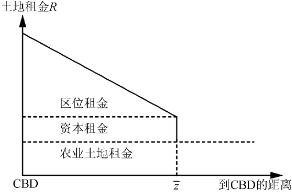
图2－5　城市地区内外的土地租金

图2－6是城市内、外的土地价格的横截面。在距离城市足够远的地方，土地以资本化的农业租金形式出售（A／r），土地仍然保持农业用途，靠近边界，土地价格将以溢价出售，溢价等于预期的土地转变为城市用地之后的土地租金升值的现价。在城市边缘，由于开发成本C，使得土地价格发生跳跃。在城市地区内部，随着到CBD距离的减少，资本化的可达性价值增加，土地价格也随之增加。

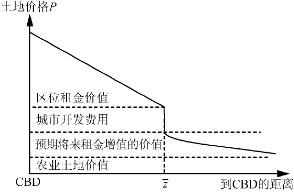
图2－6　城市地区内外的土地价格

2）Dispasquale ＆Wheaton模型

前面我们基于Capozza ＆Helsley模型分析了城市内、外土地租金和土地价值的构成，接下来我们基于Dispasquale ＆Wheaton模型来分析城市增长与土地增值之间的关系（Dispasquale ＆Wheaton，1996）。

同样假设城市位于匀质平原的几何中心，CBD集中了所有的工作机会，居民通勤至CBD。根据之前的分析，我们可以得到，在时期t，城市半径为bt时，任何城市半径区域内的区位的土地租金为：

式（2－25）中，ra为农业用地租金，bt为时期t的城市边缘，d为该区位与CBD的距离，k为单位交通费用。

假设折现率为i，在时刻t，CBD到城市边缘（固定位置）交通费用的现值为。从t＝0时刻起，城市边缘以速率g连续扩张，那么从时刻t起，CBD到未来城市边缘交通费用的现值为。连续增长的收入流的现值，如果收入是恒久的，即T＝∞，那么。当城市边缘扩张时，交通费用增加的现值为。根据租金补偿理论，交通费用的增长会造成区位租金的增加。也就是说，当城市以速率g扩张时，未来土地租金增长额的现值就是交通费用增加额的现值，即。因此，按照Dispasquale＆Wheaton模型，任何时间、任何地点的土地价格都是未来土地资金流的折现值（PDV）。假设折现率或利率为i，时间t区位d的土地价格可以表示为：

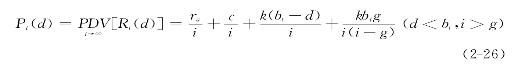
式（2－26）中，右边第一项是农业土地租金的现值，第二项是土地开发成本的现值，第三项是区位租金的现值，第四项是未来租金增长额的现值。比较式（2－22）与式（2－26），虽然二者在表达形式上存在一定的差别，但是，二者在内涵上是一致的，均说明了城市土地的价格由农业土地价值、开发成本、区位土地租金价值和增长溢价4个部分构成。

接下来，我们分析城市空间增长条件下的土地价格和土地租金的关系。比较当前（t＝0）的价格租金比，也就是式（2－26）除以式（2－25），我们可以得到：

如果城市不扩张（g＝0），那么式（2－27）右边的第二项就不存在，也就是价格租金比为折现率或利率的倒数，即；如果城市扩张（g＞0），那么价格租金比将超过。如果考虑不同的区位，由于城市边缘的

R0（d）比较小，因此式（2－27）的值就会比较大。也就是说，在城市地域范围内，越靠近城市边缘，城市土地价格增长率越高。如图2－7所示，随着城市边缘的增长，城市土地价格也会随之相应增长。假设开发成本和农业土地租金价值不变，越靠近城市边缘，城市土地价格增长的幅度越大，增长溢价的增加幅度也随之相应增大。由此可见，城市空间增长速度的变化将影响城市土地价格的变化，并且增长率g越大，所带来的增长溢价越大。

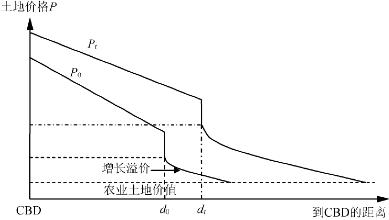
图2－7　城市空间增长对城市土地价格变化的影响

2．2．3　城市空间增长的根本驱动力

城市空间增长是一个复杂的问题，必然与诸多条件与因素有着密切的联系。基于以上构建的城市空间增长模型，我们认为人口、收入（经济）、农业租金以及交通基础设施对城市空间增长的影响最为显著。根据以上构建的竞租模型，人口增长、收入增长和通勤成本的下降是城市空间增长的根本力量。

1）人口增长

根据Brueckner的证明，在一个封闭的城市系统下，人口N对城市空间增长及其相关变量的影响为：

式（2－28）说明，人口增长引起城市空间的扩张，并且产生一个较低的城市效用水平，同时人口增长会使家庭消费的土地面积减少，并且抬高城市土地租金水平。其实，这个结论也很容易进行解释。假设城市初始状态是均衡的，然后人口增长，如此一来，在原有的城市土地价格水平下就产生了对土地的超额需求，其结果是原有的城市范围X无法容纳增长的人口，于是，整个城市的用土地租金表示的土地价格水平被哄抬起来。在消费方面，土地价格的上升导致家庭在特定区位上消费的土地面积减少；在供给方面，土地租金以及土地价格的上升导致生产者用资本替代土地，产生更高的居住密度，也就是在特定区位居住的人口增加，从而降低了城市效用水平。土地租金函数水平的上升，使城市边界也相应地外推，从而城市空间范围实现了增长。随着人口密度的增加和城市空间的增长，超额的土地需求逐渐趋于消失，城市从而实现新的均衡。基于以上人口增长对城市空间增长影响的分析，我们可以简单地认为，在其他要素保持不变的情况下，城市人口越多，城市空间范围越大；并且在任何给定的到城市中心的距离上，较大城市的建筑、人口密度以及土地租金水平更高。

2）农业土地租金下降

农业土地租金ra下降对封闭城市均衡所造成的影响与人口增长的情况类似，即：

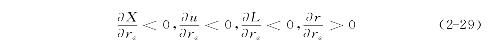
式（2－29）说明农业土地租金增加导致城市空间规模减小，城市效用水平降低，家庭消耗的土地面积减少，城市土地租金以及价格水平的上升。同样，我们也可以直观地对这一现象进行解释。假设u、r保持不变，农业土地租金水平从r′a增加到r″a，使城市边界发生相应的缩减（图2－8）。城市空间范围的减少导致了城市内对土地的超额需求，从而形成与人口增长类型相同的调整情况。需要注意的是，由于原来的城市人口被安置在一个更小的城市范围内，也就是城市变得更密集了，当城市边界X在第一轮调整（调整到xc，在图2－8中对应于r1的最终土地租金函数）后继续扩展时，也不会提高到原来的效用水平。了解农业土地租金对城市空间的影响有助于我们解释现实生活中的一些特殊的现象。例如，在其他条件相同的情况下，为何贫瘠土地地区（如沙漠地区）城市的空间范围要比位于富饶土地地区的城市大得多。

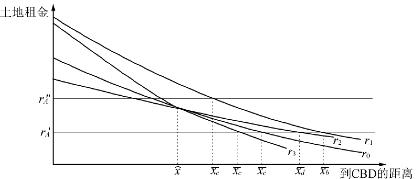
图2－8　不同要素影响下的城市空间增长情况

3）居民收入增长

城市居民收入水平的提高增加了对土地的需求，进而推动城市空间规模的增长以及居民效用水平的上升，即：

城市居民收入的提高对城市土地租金水平和居民消耗的土地面积的影响较为复杂。其中，城市土地租金函数曲线将发生逆时针旋转（在图2－8中旋转支点为且在范围内居民消耗的土地面积增加，也就说中心区位的人口密度将会下降。

总之，收入上升和人口增长对城市空间增长的作用机理相类似，在形式上都表现为城市地域范围的对外扩张，因此，二者都可以归结为城市化驱动的城市空间增长。

4）通勤成本下降

接下来我们来分析通勤成本下降对城市空间增长的影响。在一个封闭的城市中，通勤成本与城市边界和住宅价格曲线的关系如下：

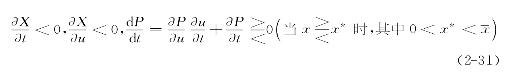
通过式（2－31）可以看出，总体上，通勤成本的下降将扩大城市的空间范围；但是，通勤成本对住宅价格（居住竞租曲线）的影响却很复杂。这可以解释为：通勤成本t的降低增加了城市内每单位土地租金和结构密度；而在较远的区位上，抬高了上述变量的值。由于，土地租金在范围内下降，在范围外下降，因此土地租金曲线以为支点逆时针方向旋转，为了简化起见，图2－8假设x＊＝x，由于通勤成本的降低在形式上表现为城市郊区化，因此称之为郊区化驱动下的城市空间增长（图2－4）。

2．3　城市空间增长模型的应用

基于竞租理论的城市空间增长模型是一个很好的经济学分析工具，这一模型可以用来分析多中心、环境质量、土地闲置和交通基础设施建设等与城市空间增长的关系。

2．3．1　多中心与城市空间增长

不少学者认为，单中心假设是竞租模型的重要缺陷，实际上，Alonso在竞租模型中已经考虑了多中心的情况（阿朗索，2007）。他以两个中心为例，分别考虑了处于竞争关系且同等大小的相邻城市中心、处于竞争关系且大小不同的相邻城市中心以及两个互补的城市中心等情形，并认为以上不同的情况对城市空间结构和城市边界的影响是不同。

如图2－9（a）所示，两个空间上相邻的竞争性城市中心，如果二者实力大小相当，并且空间距离足够接近，那么每个中心彼此的服务范围就会相交于一条直线。也就是说，两个城市的地域范围在空间上连为一体，呈现出某种形式的“双核结构”。如图2－9（b）所示，如果两个城市中心的实力存在较大的差距，并且二者在空间上足够接近，那么较小的中心B的服务区域可能被较大的中心A的服务区域所完全包围。如果B是一个独立的中心，那么其土地价格和居住密度均会比当前的实际情况低，如图中的阴影所示。

图2－9　处于竞争关系的相邻城市中心的地租模式

除了“竞争中心”之外，Alonso还阐述了“互补中心”对城市空间结构的影响。他认为城市存在不同的职能，不同的职能可能形成不同的中心，如零售中心、金融中心、制造中心等等，这些中心可能与CBD在空间上是分离的，并且形成互补关系。不同的人群在就业和通勤上可能指向不同的中心，这种指向性在他们的效用函数和通勤函数中有所体现。在存在互补中心的情况下，我们必须综合考虑一系列的空间距离，这样一来，市场均衡就相对更为复杂。以一个简单的情况为例，假设制造业中心B从原来的单一中心A中分离出来，那么势必会分离出一部分人口在B工作。假设在A工作和购物的人口的竞价函数为pi，在B工作而在A购物的人口的竞价函数为pj，不难看出，pj曲线有两个顶点，并且这两个顶点分别与两个中心相对应。根据曲线pi和曲线pj的关系，制造业中心B的分离对城市空间结构的影响可能存在不同的情况（图2－10）。如图2－10（a）的阴影区所示，工作和购物都在A的人口在中心A附近聚集，并且被工作在B而购物在A的人口所包围，通常而言，在中心A附近工作和购物的人口为高收入阶层，因为他们愿意为居住在中心A附近而支付更高的土地租金。当然，也存在另外一种情况，在两个中心合力的作用下，部分在中心B工作的人口可能会愿意为居住在中心A附近而支付更高的土地租金，那么中心A附近的区域可能被在中心B工作而在中心A购物的人口所占据（图2－10（b））。

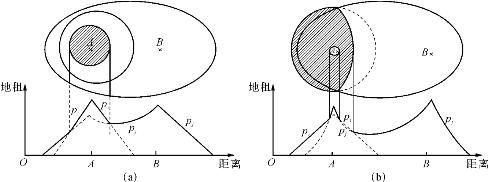
图2－10　处于互补关系的相邻城市中心的地租模式

2．3．2　土地闲置与城市空间增长

按照前述的城市空间增长模型，城乡边界为城市土地租金等于农业土地租金加上土地开发成本的点。然而，在现实生活中，我们经常看到似乎相互矛盾的现象：一方面，城市内部存在大量的闲置或农业用地，另一方面，实际的城市土地开发往往超过理论上的城市边界，延伸到农业用地之中。Mills等将这种现象称之为城乡用地的“模糊边界”，并且认为有三个因素导致这一问题的发生：第一是农业生产率并不是同一的，城市边界之内某些地块的农业生产率相对较高，从而维持农业生产是有利可图的，而城市边界之外的某些地块的农业生产率相对较低，将其转变为城市用地也是合理的；第二是农场主倾向于在特定的时间段交易农业土地，例如在退休前农场主交易土地的意愿更为强烈，这样就延缓某些农业土地转变为城市用途的时间；第三是土地投机行为，在经济快速发展和城市空间迅速增长时期，城市土地增值预期很高，土地市场中的投机活动十分盛行，土地所有者因而不愿将土地出售或者长期出租，而宁愿让其闲置或作为绿化用地（Mills，1994）。

土地投机活动盛行，不仅使城市内部大量土地闲置，而且也推动了城市空间增长。如图2－11所示，由于土地投机盛行，大量城市土地闲置，也就减少了土地市场中有效的土地供应量，反过来又抬高了城市所有区位的土地租金，也就使竞租曲线外移，从而使城市边界相应外移。由此可见，土地投机及其所导致的土地闲置问题的普遍存在，在不断自我推高土地租金和价格的过程中，也使城市空间不断扩展，而这一过程也是土地价格泡沫形成与膨胀的主要路径。

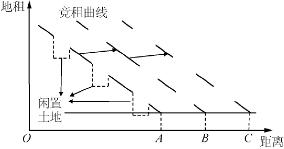
图2－11　土地投机盛行下的竞租曲线与城市边界

2．3．3　环境质量与城市空间增长

在现实生活中，家庭进行居住区位选择要考虑很多因素，环境就是其中重要的因素之一。环境的变化不仅会影响家庭的居住区位选择，而且也会对城市空间增长与结构产生影响（麦卡恩，2010）。

假设由于人口过度聚集导致城市中心的居住环境恶化，并且与城市中心距离越远，环境质量越好。我们将环境质量定义为E＝f（x），其中E代表环境质量；f（x）表示环境质量，是与城市中心距离的函数。假设环境质量是与距离无关的公共产品，那么E与该区位消耗的土地数量无关。在土地和非土地要素投入水平既定的情况下，我们可以把环境质量的提高看作效用的增加。于是，我们可以把环境质量加入到家庭效用函数中，即：

相应地，约束条件变为：

均衡的条件为：

不难看出，式（2－34）的符号取决于括号内的部分，即竞租曲线的斜率和形状取决于环境质量改善的收益和距离增加带来的交通成本的对比情况。如果距离增加所带来的环境质量改善的收益大于距离增加所带来的交通费用的增加，那么竞租曲线将向上倾斜；反之，如果环境质量的改善不如距离的交通成本显著，那么竞租曲线的斜率仍然为负，不过曲线变得比较平缓。由此可见，环境质量对城市空间结构和边界均会产生实质性的影响。如图2－12所示，城市中心的环境质量情况对城市土地的竞租曲线的影响是不同的，城市边界也发生相应变化。总体上而言，城市中心环境污染的推力和农村优美环境的拉力倾向于扩大城市边界，也就是更多的城市空间增长。

2．3．4　交通基础设施建设与城市空间增长

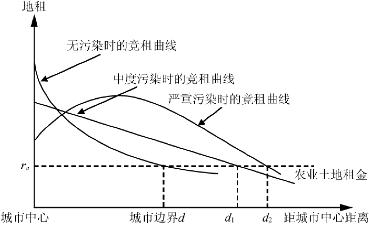
图2－12　环境质量对城市空间结构和城市边界的影响

Brueckner（2003）和丁成日（2005）认为，在城市总人口不变的情况下，由于交通的发展（如高速公路的建设）使城市土地地租曲线逆时针旋转，称之为城市郊区化带来的空间外延。笔者认为，这只是交通基础设施影响城市空间增长的路径之一，交通基础设施对城市空间增长的影响远比此复杂（洪世键，2010）。

假设地方政府出资修建了一条由市中心O通往郊区A的公路。公路的修建，减少了城乡之间的通勤成本。假设所有的交易均在城市中心发生，因此通勤成本的降低对商业和工业没有影响。如前所述，在一个封闭的城市中，总体上，通勤成本的下降将扩大城市的空间范围；但是，通勤成本对住宅价格（居住竞租曲线）的影响却很复杂。这可以解释为：通勤成本的下降降低了城市中心区位上每单位住宅的价格、居住土地租金和结构密度；而在较远的区位上，抬高了上述变量的值。由于住宅价格在范围内下降，在x＊范围外下降，因此住宅价格曲线以x＊为支点逆时针方向旋转，居住竞租曲线也发生相应的旋转。为了分析的便利，假设x＊为工业用地和居住用地的分界点，于是旋转之后的居住竞租曲线R′3如图2－13所示。

此时，城市边界应该外推至点x′。但是，考虑到基础设施是由地方政府出资修建的，其成本要计入土地开发成本之中，因此，实际上竞租曲线的均衡点上升为r＝ra＋iD′－s，相应地，城市边界点也由点x′变为点x″^[1]。同时考虑到公路修建所产生的通勤成本的下降具有空间衰减的

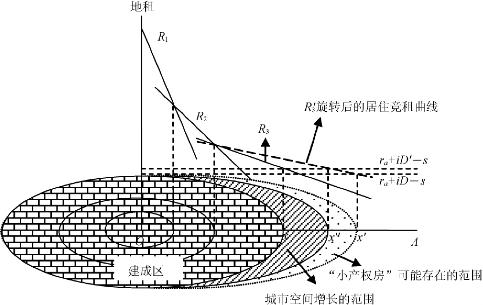
图2－13　公路基础设施建设对城市空间增长的影响示意图

特征，也就是距离道路越远，通勤成本下降的幅度越小，因此，由地方投资的连接城乡的公路对城市空间所产生的影响是沿着公路的方向拉升了城市的空间范围，即图2－13［x，x″］之间的阴影部分^[2]。图2－13［x″，x′］范围内区域，对于地方政府而言，进行城市土地开发是不经济的；但是对于开发商而言，由于不需要承担交通基础设施的修建成本，因此建造住宅仍然是有利可图的。这样一来，在这一地带就有可能发生开发商未经政府的征收和出让手续而自行从农民手中租用土地开发房地产的现象，这就是所谓的“小产权房”。因此，基于本书的分析视角，我们认为“小产权房”可以看做是交通基础设施外部性效应的结果。

如果修建的交通基础设施不是公路，而是轻轨等轨道交通，那么其对城市空间增长的影响会与公路有所不同。由于在这些轨道交通站点周围通勤成本的下降更为明显，因此居住竞租曲线在这些站点形成偏折，并且偏折程度随着站点与城市中心距离的增大而变小。这样一来，在郊区的轨道交通站点周围形成一定范围的居民区，从而使城市将以“珍珠项链”方式扩展（图2－14）。

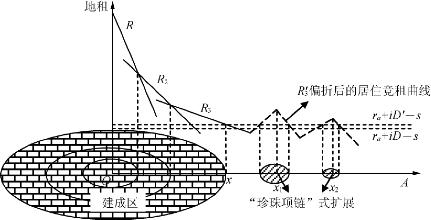
图2－14　轨道交通基础设施建设对城市空间增长影响示意图

【注释】

[1]假设交通基础设施修建成本很高，以至于对于地方政府而言，增加的土地开发成本超过了城市空间扩展的收益，那么修建交通基础设施就是不经济的，城市空间也就不会发生增长。

[2]交通基础设施的建设对城市内部的空间结构也会产生一定的影响，但这不是本书的重点，因此不予讨论。