采用NGSIM项目中主干道Peachtree Street路径S1→E11方向6个检测点从2006年11月7日至11月9日连续3日采集的24 h交通流量数据对模型进行验证。以第1天和第2天的数据为输入数据、第3天的数据为验证数据。为保证神经网络快速稳定的学习，输入和输出数据被线性缩放到区间［0．1，0．9］中。
应用Matlab R2010b软件中神经网络工具箱和卡尔曼滤波工具箱中的相关函数对状态空间神经网络和扩展卡尔曼滤波模型(State Space Neural Network and Extended Kalman Filter Model，SSNNEKF)进行编程实现。状态空间神经网络采用Levenberg-Marquardt方法进行训练。对SSNNEKF模型，有两类参数是需要进行初始化设定的:神经网络权重系数和滤波噪声。通常来说，这两类参数是凭经验设定的，在没有先验经验时，这两个参数采用随机数，并通过大量的训练数据对其进行标定可以发现，类似于其他启发式算法，SSNNEKF模型的参数在初始阶段预测值和观测值的差异较为明显，但经过一定时间的训练后，误差会显著下降到一个可以接受的区域内。
为验证SSNNEKF模型的精度和稳定性，将BP神经网络和状态空间神经网络模型作为参照模型对SSNNEKF模型进行验证。误差指数由式(2-23)和式(2-24)所确定。
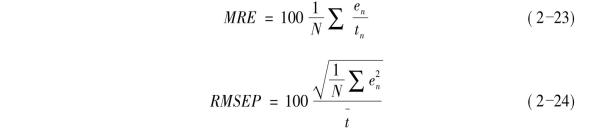
式中：e——预测误差;
t——测量值;
N——预测段的总数。
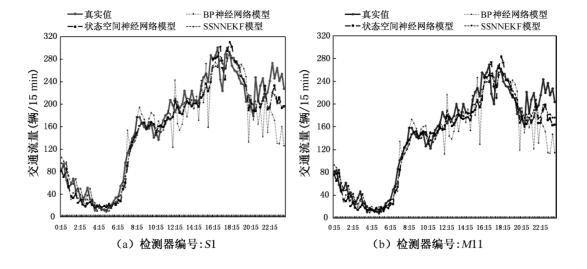
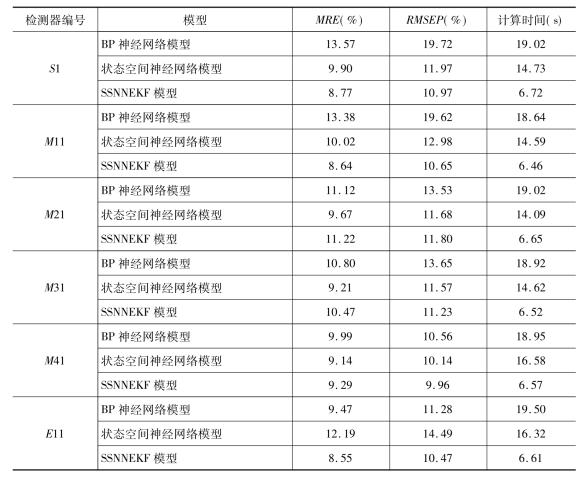
图2-17分别给出了BP神经网络、状态空间神经网络模型和SSNNEKF模型的短时预测值和真实值之间的比较结果。图 2-18和表 2-1给出三种模型的误差分析指标。状态空间神经网络模型和SSNNEKF模型的估计结果没有太大的区别，但训练效率有了很大程度的提高，这说明应用扩展卡尔曼滤波训练状态空间神经网络模型可以在不降低模型预测精度的前提下极大地提高模型的训练效率。SSNNEKF模型的训练时间也远远低于状态空间神经网络和BP神经网络模型。测试结果表明，SSNNEFK模型比其他两种模型具有更好的鲁棒性。
(www.xing528.com)
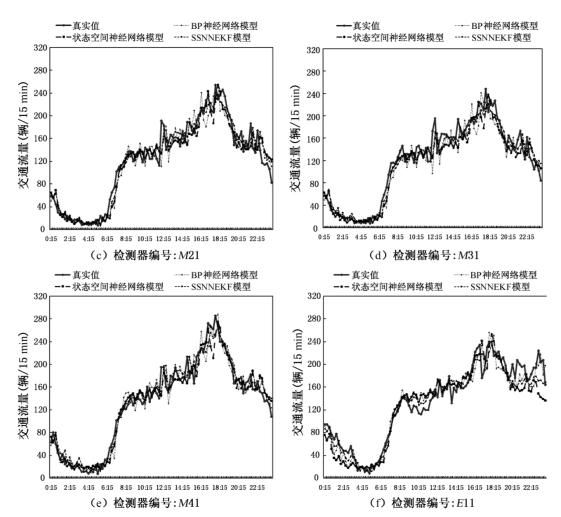
图2-17 三种模型测试结果比较
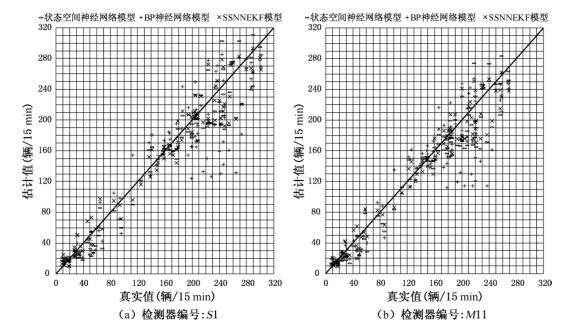
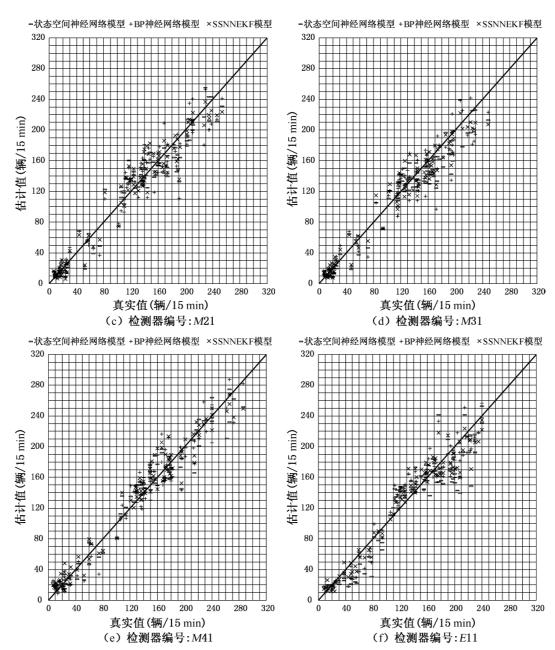
图2-18 三种模型误差分析比较
表2-1 模型测试结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
