城市交叉口群交通控制方法

1．状态空间神经网络

状态空间神经网络(State Space Neural Network，SSNN)起源于艾尔曼提出的递归神经网络(Recurrent Neural Network，RNN)［157］。递归神经网络能通过调节各神经元权重来高效地学习复杂的时空状态。和传统的神经网络不同，状态空间神经网络通过添加一个储存之前神经元状态的状态层作为短期记忆层，以使神经网络能根据当前时刻的状态和前一时刻的状态决定预测输出值，能更高效地学习复杂的时空状态。状态空间神经网络的概念类似于马尔科夫链，每当一个时间点的状态被输入神经网络，各神经元的计算类似于前反馈网络。不同的是状态空间神经网络的输入包括反映之前时间点神经网络内部状态的变量，即每当之后一个时间点的状态被输入状态空间神经网络时，其隐含层的神经元和输出层的神经元单位的状态值由之前时间点神经网络的状态计算得出。状态空间神经网络的拓扑图如图2-15所示［158］。

通过状态空间神经网络的数学描述可知，隐藏层的向量s(t)为输入向量和偏差加权和，其可通过传递函数式(2-16)由输入层向量x(t)计算得出。

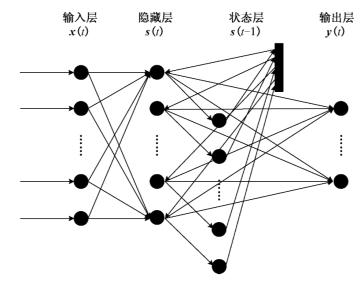
图2-15　状态空间神经网络拓扑结构

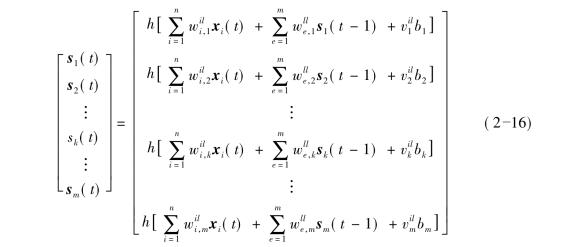
式中：sk——第k个隐藏层神经元的值;

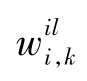　——连接第i个输入层神经元和第k个隐含层神经元的权重;

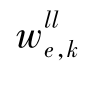　——连接第e个隐藏层神经元和第k个状态层神经元的权重;

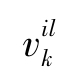　——与第k个隐藏层神经元的偏差值权重;

　bk——第k个隐藏层神经元的偏差值，其定值为1;

　h(·)——传递函数。

传递函数h(·)采用非线性的Sigmoid函数，其作用在于将结果之和转化到区间［0，1］中，如式(2-17)所示:

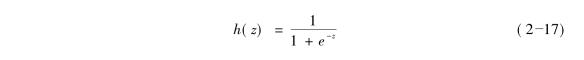
输出层向量y(k)可由式(2-18)计算而得:

式中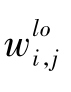：——连接第j个隐藏层神经元和输出层神经元的权重;

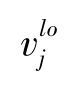　——链接输出层神经元的偏差值的权重；(www.xing528.com)

　bj——隐藏层神经元的偏差值，其定值为1。

2．基于扩展卡尔曼滤波的状态空间神经网络训练方法

状态空间神经网络因为其良好的特性可被用于短时交通信息预测，但是其训练数据效率较低，因此可选用其他方法对其训练，在保证模型精度的同时减少神经网络的训练时间。扩展卡尔曼滤波模型可同状态空间神经网络相结合，提升其训练效率。

整个神经网络的系统状态可以表达为如下非线性离散系统:

式中：θk——神经网络的权重系数，可以看成一个静态的过程;

　ωk——过程噪声;

　yk——观测向量;

　vk——观测噪声;

　g(·)——非线性状态函数。

根据泰勒公式展开，式(2-19)可以用状态估计量表达为如下的形式:

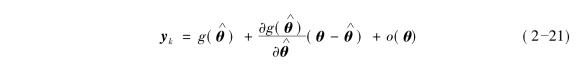
忽略掉高阶部分，扩展卡尔曼滤波就能够通过迭代公式(2-22)来训练神经网络:

每一个计算时刻，输入向量xk代入到公式(2-16)、(2-17)和(2-18)中，就得到输出向量。根据误差向量计算得出微分矩阵Hk。再由Hk计算得出卡尔曼增益矩阵Kk，其中，PkPk和Rk为误差协方差矩阵和测量值协方差噪声矩阵。神经网络权重系数的更新是根据增益矩阵、误差向量和当前的权重值而得到。状态空间神经网络和扩展卡尔曼滤波的模型拓扑结构如图2-16所示。

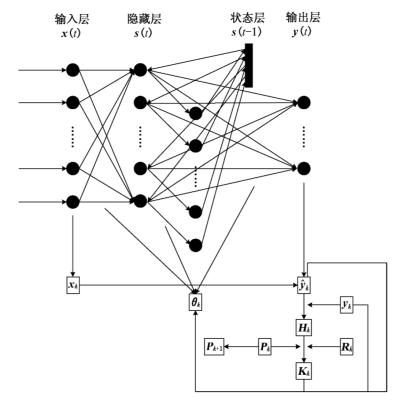
图2-16　状态空间网络和扩展卡尔曼滤波模型拓扑结构示意图