城市交叉口群交通预测与控制方法

在交叉口群静态交通控制优化过程中，要求整个协调控制区域内所有需要的交通流参数都是已知的。而在交通动态协调控制中，由于交叉口群中各检测器所采集的交通流参数不同，检测器布设的位置也有不同，部分交通流参数可能无法直接实时获取。对于无法直接获取的交通流参数需要应用模型估计或者离线标定的方法来确定。因此在交叉口群交通信号动态协调控制中，表征交通信息的交通流参数的估计和预测是相当重要的研究内容，参数的估计方法和精度会对控制策略的效果产生很大的影响。

根据预测的基本方式的不同，短时交通流预测模型可以分为数据驱动(Data Driven)和基于模型(Model Based)两种类型。

数据驱动的方法用数理统计或人工智能的方法处理，如交通流量、交通速度、行程时间等的历史交通数据，并预测未来时段交通流的变化。常用的模型包括历史平均模型(History Average Model)、线性回归模型(Linear Regressive Model)、时间序列模型(Time Serial Model)、卡尔曼滤波模型(Kalman Filter Model)、马尔科夫预测模型(Markov Model)、极大似然估计模型(Maxium Likelihood Formulation Model)、非参数回归模型(Nonparametric Regression Model)、神经网络模型(Neural Network Model)、混沌理论模型(Chaos Theory Model)等。这类模型一般假设未来预测的数据和历史数据有相同的特性，根据历史交通数据的变化规律来预测未来的数据。

基于模型的方法主要应用交通流传播模型对确定路径上的交通流状态进行估计和预测。按照模型对于交通流描述的细致程度，可将模型分为宏观模型、中观模型和微观模型三种。宏观模型和中观模型指出在某条路径上某时刻在某点处的交通参数s(t，x)，除了与时间t、位置x有关外，还与该时刻之前该位置处交通变量值s(t－1，x)以及该点上下游相邻处交通变量s(t，x－1)、s(t，x +1)有关，即交通流过程是交通变量随着空间、时间而演变的动态过程。在该动态过程中，流量、速度和密度三个变量的数值之间不存在严格的对应关系(和稳态交通流不同)，所以完整的模型应是三者的结合。在有些情况下，只取某一个或两个变量的模型也可对相应的变量进行控制。

1．一般模型

应用神经网络等人工智能式算法预测短时交通流参数的方法最大的弊端在于:传统的神经网络只应用历史数据来预测未来的交通流参数，而不能反映实时的交通流参数变化。应用状态空间神经网络来预测短时交通流参数变化，能综合考虑当前时段和历史的交通流参数变化特征，准确、快速地预测交叉口交通流短时变化特性。

应用状态空间神经网络预测短时交通流状态的本质为通过交叉口群中各个交叉口的历史交通数据和实时交通数据预测下一时段的交通流状态。交叉口短时交通量预测的一般模型如式(2-14)所示，其中各交叉口的状态可设为影响未来交通流参数变化变量的函数，如式(2-15)所示。

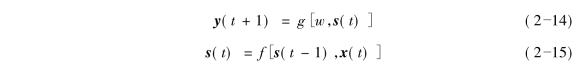
式中：s(t)——t时段交叉口群交通流状态;

　x(t)——描述影响交叉口群的交叉口在t时段的各观测变量的向量(如交通量、占有率、车辆速度等);

　y(t+1)——预测t+1时段的交通流状态;

　w——权重系数;(www.xing528.com)

　f(·)和g(·)——传递函数。

2．短时交通流预测的状态空间模型

交叉口群交通信息的短时预测和交通量、占有率、平均车速等观测变量在空间和时间上的变化都有着直接联系。状态空间模型类似于宏观交通流模型中路段交通流状态由当前状态和之前状态综合计算而得，其t时刻的输出结果是由t时刻的状态空间以及t－1时刻系统的状态综合计算而得。

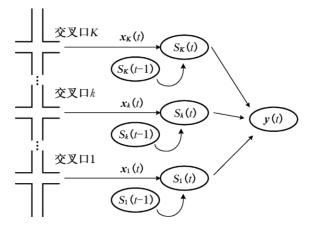
图2-14　交叉口群的动态状态空间结构

建立交叉口群短时交通流预测的状态空间模型如图 2-14所示，道路沿线的第k个交叉口动态的状态空间可用以下方法来定义。交叉口k在t时刻的状态sk(t)可由t时刻的观测值xk(t)和交叉口t－1时刻的交通流状态sk(t－1)定义而得。以此类推，t－1时刻交叉口k的交通流状态由［t－2，t－1］时段模型输入转换而来。每个时段模型的输入为当前所有观测变量的总和:x={ x1(t)，…，xk(t)，…，xK(t)}。

交叉口k的状态向量sk的值基于函数f(·)的选择。向量xk(t)反映了交叉口k在时段t的交通流变化状况。基于一般模型选用不同传递函数f(·)及g(·)推导出不同的状态空间模型［153］。

(1)ARMA模型:令xT(t)=xT(t)，g(·)为线性函数，再令f(·)为恒等函数(即f:x→x)。关于ARMA模型的详细介绍请参见相关文献［154］。

(2)线性状态空间模型:f(·)和g(·)均为线性函数，详细例证参见线性控制理论［155］。

(3)非线性状态空间模型:假设f(·)为非线性函数，g(·)为线性函数或非线性函数，宏观交通流理论中有类似的求解问题，非线性状态空间模型可用特定的递归神经网络求解［156］。

短时交通流预测的影响因素均为非线性变量，因此模型的输入变量是非线性的，由此可知交叉口短时交通流预测模型属于非线性状态空间模型，可选用特定的递归神经网络求解，如状态空间神经网络可用于求解此模型。