城市交通动态协调控制方法-路径行程时间理论构成

车辆在信号控制交叉口群中的行程时间受道路几何线形、交通流量、交通流组成、交通管制等因素的影响，对于某一条有信号控制的交叉口群路径，行程时间由三部分构成:在路段上的自由行驶时间、在交叉口的排队时间、由于车辆排队等候从自由行驶速度减速至静止及加速至自由行驶速度的时间。

路段和交叉口是组成路径的两个基本物理单元。交叉口的概念容易理解，不会产生歧义，而路段则因所研究的问题不同而有不同的划分方法。此处以停车线为基准，将路段定义为同一道路同一方向的相邻两个交叉口停车线之间的路程，即将一个交叉口及其相连的下游路段划分为一个分析路段，这样每个路段都含有一个交叉口。一个路段可以被划分为驾驶区和排队等待区，这是两种运动形式。如果一个路段没有排队等待区，如图2-9中的路段a，则该路段的驾驶区可与下游路段的驾驶区合并，因此驾驶区不会受到路段长度的制约，为此将车辆一次完整的行驶距离称为间隔行驶距离。

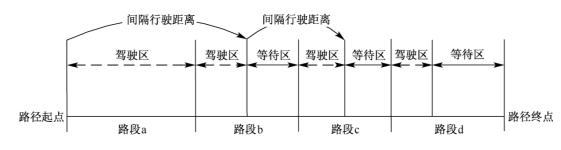
图2-9　路段驾驶区与排队等候区划分

车辆在驾驶区内行驶会出现速度上的变化，一种较为典型的情形是:车辆以稳定的加速度离开某个排队等待区驶向下游的驾驶区和等待区，有可能的话会达到交通条件所允许的最高限速，而后又以稳定的减速度从最高限速降低至零，转向下游队列;此外也有可能在达到最高限速之前就开始减速，这一特征为行程时间的分析提供了线索。

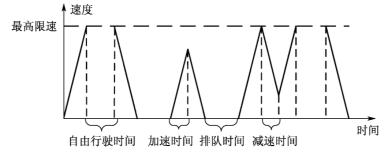
图2-10　行程时间与速度关系

图2-10给出了几种典型的行驶特征。最左边的梯形表示车辆从上游交叉口停车线静止启动，加速至最大速度自由行驶一段时间后，减速至静止，在下游交叉口排队车队后等待;接下来的小三角形表示车辆在从静止启动后没有达到最高限速就到达下游交叉口排队等待区;而后是一个可以瞬间到达最高限速的三角形，驾驶员在看到前方有车辆排队后开始减速，但尚未静止时下游交叉口信号灯切换为绿灯，排队车辆获得通行权开始启动加速，驾驶员跟随前方排队车辆开始加速并达到最高限速，直至到达下一个排队等待区。图中可反映出若干与行程时间相关的重要特征:①无论梯形还是三角形，每个区域面积都代表一个驾驶区内的行驶距离，但不一定是一个分析路段的长度;②相邻两个排队间隔时间的长度不一定相等，但却是相关的;③并非所有车辆在任何路段都能达到其允许的最高限速。下一节将采用实地观测数据对某条路径上车辆行程时间的相关特征予以进一步验证与说明。

以下建立行程时间的估计模型［153］。记每一条路段长度为li，i=1，2，…，n，R(i)为路段上没有被车辆占用的区域，则路段的排队长度为q(i)=l(i)－R(i)。yj和Ti(j)分别是第j个间隔行驶距离和相应的行程时间。如果在路段i上存在队列q(i)，y(i)=q(i)+ R(i + 1)，否则y(i)=q(i－1)+ li+ R(i + 1)。据此，在第i条路段上的第j个间隔行驶距离内的行程时间Ti(j)可表示为:

式中：k——车辆从静止加速到最大速度所需时间;(www.xing528.com)

　s——所能达到的最高限速。

对于梯形，Ti(j)可以很容易得到，而对于三角形，不论能否达到最高限速，根据物理学中的位移定理，也可从上式得到。如果在一条路径上存在r个间隔行驶距离，则在这些区间内的行程时间可表示为:

此外，在该路径上的排队时间可以简单地表示为:

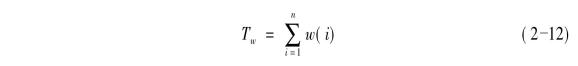
式中:w(i)——第i条路段上的排队时间。

由于信号周期是确知的，因而Tw不难获得。因此在该路径上的完整行程时间为:

显然T是一随机变量，上述所设计的行程时间估计方法同时考虑了行驶和等待时间。