城市交叉口动态协调控制方法

交叉口群网络中不同路径车流运行特征的交叠增加了交通流信息分析的难度。采用时间序列数据挖掘(Time Series Data Mining，TSDM)工具，考虑数据集之中数据间存在的时间关系，从真实的、大量的、含噪声的数据源中揭示出隐含的、先前未知的并有潜在价值的信息，是交通流信息处理与分析的重要手段之一。对交通流信息进行相似性比较，可用于揭示交通流信息的周期性变化规律，通过比对历史数据检测交通事件的发生，在数据存储时压缩冗余成分［143～146］。研究选用时间序列相似性搜索方法中的动态时间弯曲距离(Dynamic Time Warping，DTW)度量交叉口群内多个检测点交通流量信息在空间维度与时间维度上的相似程度，用以区分车流的走向，揭示交通流量信息沿前行路径方向的传递规律。

1．时间序列相似性搜索原理

所谓时间序列相似性搜索，就是找出与给定查询序列的变化行为最为接近的数据序列。给定一个目标模式X=(x1，x2，…，xn)和一个序列Y=(y1，y2，…，ym)，相似性问题就是如何确定X和Y的相似度sim(X，Y)。n和m的取值可以相同也可以不同，当n=m时是两个序列完全匹配(whole sequence matching)的问题，即从具有相同长度的序列中查找相似的序列;当n≠m时为子序列匹配(subsequence matching)问题，即从yi(i=1，2，…，m－n + 1)开始，找出Y中与X最相似的子序列(假定n＜m)。

无论哪一种相似性的搜索都依赖于时间序列的相似性度量方法，即如何定义sim(X，Y)。目前时间序列相似性的度量主要是基于距离的度量。给定一个计算序列间的距离公式，并确定一个距离阈值，对任意给定的两序列，当距离小于或等于阈值时，则认为两序列相似，否则，认为二者不相似。因为长度为n的时间序列可以看做是n维空间上的点，所以空间距离函数可以用作序列距离公式，而最困难的是如何定义序列间的距离。在时间序列相似性搜索中最常用的是欧几里得距离(Euclidean distance)，也称欧氏距离。

设两组单变量时间序列分别为X=(x1，x2，…，xn)和Y=(y1，y2，…，ym)，当n=m时，它们的欧氏距离定义为:

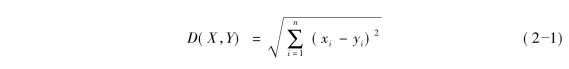
欧氏距离虽然比较简单，但是在相似性的度量中却很不可靠，这是因为时间轴的微小变形将会引起欧氏距离很大的变化，因此对时间轴有轻微变形的时间序列相似性的测量，欧氏距离将不再适用，如图2-3所示。虽然两个时间序列的形状相似，但是它们在时间轴上并不是完全对齐的，因此图2-3(a)中用欧氏距离计算相似性结果的距离将会很大，可能会导致产生不相似的结果。

在交叉口群路径交通流量信息的分析过程中，上、下游检测点获取的信息由于时滞的存在，在时间轴上并不完全对齐，可以采用固定的时滞值对时间轴进行平移后再计算欧氏距离，但由于驾驶者行驶速度的不一致性，时滞值在一定范围内浮动，特别是当采用较小的统计间隔时计算结果往往并不理想。若测量时，时间轴可以根据具体情况进行移动，在两个序列之间寻找一条对齐路径，使得两个序列之间的欧氏距离最小，从而更直观(更类似于人类思考方式)地测量时间序列的相似性，会更有效地找到两个时间序列的相似形状。对于这种情况人们提出了一种新的相似性测量方法——动态时间弯曲距离(Dynamic Time Warping，DTW)法，该方法允许在时间轴上有弹性地移动，以便能够在两个时间序列的不同时间阶段发现相似的波形。动态时间弯曲距离可以适时地转换、扩张或压缩两个序列的局部特征，实现两个序列的同步化，因此动态时间弯曲距离不要求比较序列长度的一致性。

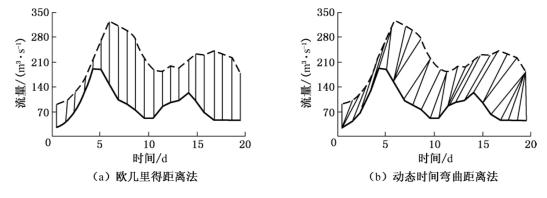
图2-3　不同的距离度量方法

2．DTW距离算法

设两组单变量时间序列分别为Q=(q1，q2，…，qi，…，qn)和C=(c1，c2，…，cj，…，cm)，n和m分别为时间序列Q和C观测值个数(见图2-4)。构建一个n× m阶的矩阵，其中，第(i，j)个元素是两个时间序列的点qi和cj之间的距离d(qi， cj)，d(qi，cj)的计算采用欧氏距离，即d(qi，cj)=(qi－cj)2。

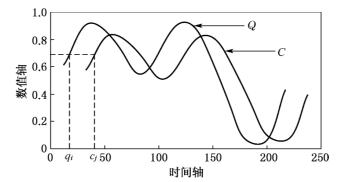
图2-4　两组相似的时间序列(www.xing528.com)

如图2-5所示，一条弯曲路径W是由上述矩阵元素构成的连续路径，这条路径定义了时间序列Q和C之间的一个映射，W的第k个元素的坐标被定义为wk=(i，j)k，可得到一个路径集为:W={ w1，w2，…，wk，…，wK| max(m，n)≤K＜m +n－1}。该路径满足以下条件限制［147］:

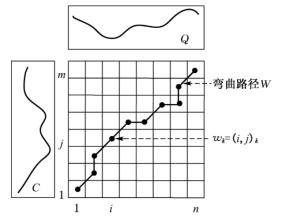
图2-5　弯曲路径示意图

(1)边界条件:w1=(1，1)且wK=(m，n)，即要求弯曲路径必须从矩阵的起始位置处开始到对角的结束位置处结束;

(2)连续性:给定wk=(a，b)和wk－1=(a'，b')，要求a－a'≤1且b－b'≤1，即要求弯曲路径每一步的设定都是连续的;

(3)单调性:给定wk=(a，b)和wk－1=(a'，b')，要求a－a'≥0且b－b'≥0，即要求路径必须在时间轴上是单调的，也就是说路径W通过点(i，j)的同时必须至少通过点(i－1，j－1)，(i－1，j)或(i，j－1)中的一个。

满足上述条件的路径有很多条，可计算每条路径到达点(m，n)时总的累积距离，选择具有最小累积距离者为最佳路径，即

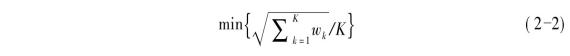
式中：K——路径W的长度，用以消除不同弯曲路径长度的影响。

如果点(i，j)在最佳路径上，基于动态最优原理可知，从点(1，1)到点(i，j)的子路径也是局部最优解，也就是说从点(1，1)到点(m，n)的最佳路径可以由时间起始点(1，1)到终点(m，n)之间的局部最优解通过递归搜索获得。构造累积距离矩阵γ，点(i，j)的计算公式如下:

式中：d(qi，cj)——两个时间序列对应点qi和cj之间的距离。

其初始条件为γ(1，1)=d(q1，c1)。从两个序列起始点(1，1)开始迭代计算点(i，j)的累积距离，最终时间序列弯曲路径最小累加值γ(m，n)为时间序列Q和C最佳路径的DTW距离，即DDTW(Q，C)=γ(m，n)。