培根与波普尔的归纳与猜想反驳

第4章　是培根的归纳还是波普尔的猜想－反驳

BACON系统的开发者认为BACON重新发现经验定律的方法，就是培根所提倡的归纳方法。他们对培根的归纳方法是这样理解的：“培根相信，如果一个人收集到足够的数据，那么在这些数据中的规律就会跳出来（leap out，原文用斜体字），呈现在观察者面前。BACON．3这个程序正是用这种方法发现经验定律的［4］。”于是，他们将该发现系统以这位早期科学哲学家的名字来命名。

与此针锋相对，科学哲学研究者孔宪中认为：“从一开始，BACON做的工作根本就不是归纳。拿BACON．1再发现开普勒第三定律来说，它所做的就是去检验假说，一个接一个地。第14个假说因为经受了检验而被接受，而前面13个假说都失败了。这是典型的假说－演绎方法，波普尔的证伪方法［19］。”所以他认为“BACON”这个名字用得不当，而且具有讽刺意味，因为BACON运用的方法恰恰是将自己同培根作了坚决划分的波普尔的猜想－反驳方法。

第1节　BACON方法对归纳思想的意义

1．BACON、培根的归纳、现代归纳逻辑

培根的归纳方法是以机械的步骤和致力于万无一失的目标为特征的，通常又被称为“机械的归纳方法”或“三表法”。培根的科学发现方法包括三个步骤［98］：第一步是收集“要充分还要好”的观察和实验数据和事例，培根称为“自然和实验的历史”。这是一切的基础。第二步，按某种方法和秩序把观察和实验事例制成表和整序，即建立培根所说的三张表：存在表、不存在表和程度表，这样就将纷繁复杂的“自然和实验的历史”整理为人的理智能处理的东西。第三步，运用培根的“真正的合格的归纳法”从表中归纳出科学结论。

培根的归纳，不允许理智在未经对所建表中的事例进行仔细考察就由特殊的东西跳到和飞到普遍原理上，他说，“对于理解力不可赋以翅膀，倒要系以重物”。培根的归纳是从观察实验的事例出发，“遵循一个正当的上升阶梯，不打岔，不躐等，一步一步，由特殊的东西进至较低的原理，然后再进至中级原理，一个比一个高，最后上升到最普遍的原理；……［98］。”

在这里，我们以培根的方法与BACON的方法相对比，发现二者非常相似。在重新发现理想气体定律中，BACON．3被给予关于P（气体压强）、V（气体体积）、T（气体的开尔文温度）和n（气体的摩尔数）之间相互变化关系的一堆实验数据，BACON．3首先探测到P和V之间的关系，并定义PV这个理论词项（也可以看作是BACON．3发现的较低原理），接下来，BACON．3将PV作为变量，考察它对T的关系，于是发现PV/T这个更高一层次的理论词项，也即一个较高原理，这样逐级上升，描述层次不断增加，最终得到pV/nT＝K这一经验性的、描述性的普遍原理。而且正如培根对他的归纳做的继续说明：

最低的原理与单纯的经验相差无几，最高的、最普遍的原理（指我们现在所有的）则又是概念的、抽象的、没有坚实性的。唯有中级公里却是真正的、坚实的和富有活力的，……，正是依靠着它们，也只有由它们而上，到最后才能有那真是最普遍的原理，这就不复是那种抽象的，而是被那些中间原理所切实规限出的最普遍的原理［98］。

BACON系统迄今仅限于能发现经验性的，描述性的定律，它们在整个科学理论体系中，就相当于培根所说的真正坚实而有活力的“中级公理”，而由它们所规限出的理论体系才不仅是抽象的，并且是切实反映自然界本质的最普遍原理。

我们知道，古典的培根传统归纳逻辑与现代归纳逻辑有一个重要区别，那就是在自然科学中运用归纳推理的目标发生了质的改变。培根传统下的方法论家致力于追求发现真理，而现代的归纳逻辑研究者已经将这个目标转变为最大限度地接近真理，具体体现在：知道尽可能多的真理，或尽可能地接近于某一问题的真实答案，或得到尽可能大的把握真实答案的机会等等。

但是，培根的归纳逻辑有一个传统一直保留下来，并在上面分析的BACON程序中得到运演。培根不仅仅寻求发现真理，还寻求发现规律。在达到最高级的普遍真理之前，要经过培根的“较低原理”到“较高原理”，一步一步逐级上升的过程，在这个过程中，随着证据的变化而导致归纳等级的变化，人类的智慧就这样通过“形式（即培根的规律）”的等级而进步。

相应地，在现代归纳逻辑的发展中，人们认为应当使培根归纳逻辑的这一中心思想系统化。现代归纳逻辑代表性人物之一乔纳森·柯恩（L．Jonathan Cohen）提到这种工作的两个主要构成步骤：首先，需要包括一种“相关变元的方法”，用来表示在任何特定的研究领域中，一个假说的可靠性依据适当变化的实验证据进行分级的方式。其次，需要包括一般模态逻辑，这种逻辑将把可归纳证实的可靠性的等级表示为通向规律陈述的阶梯上的梯级［93］。这种发展现代归纳逻辑的路径也被称为“新培根归纳逻辑”系统，它与卡尔纳普（Rudolph Carnap，1891～1970）归纳逻辑系统的区别在于，前者着眼于逻辑的物理学意义，而后者着眼于语言学意义。因此，新培根归纳逻辑能为自然科学中的实验推理提供一个比之其他系统更好的表述。

图4－1　弗兰西斯·培根
（图片来源：The Internet Encyclopedia of Philosophy
www．utm．edu/research/iep/b/bacon．htm．［2008－03－11］）

而BACON程序的检验表明，将实验证据进行分级、归纳形式逐级上升，是一个有效的发现经验规律的发现模式，BACON就是在不同层次的描述簇（即实验数据）基础上，在一种情况下，依次发现了波义耳定律、理想气体运动定律等不同层次的定律；在另一种情况下，像伽利略一样，先发现单摆的周期同它的支撑物长度关系的定律，以及伽利略的更有名的匀加速定律（uniform acceleration law），随后将两个定律的描述簇归并到一个更高层次的描述簇中，进而发现了单摆和加速度的关系定律。可见，培根归纳逻辑中的一些思想的确值得在现代逻辑发展中进行系统化的探索。

2．BACON：阅读大自然不是诠释大自然

孔宪中对BACON使用的启发式搜索方法的描述，AI科学家是不会赞同的。西蒙早在80年代来北京讲学期间，就将启发式搜索方法与假说－检验方法用非常直观的例子做了明确区分［12］。另外一位AI之父，明斯基也曾明确区分启发式搜索和那种不受时间约束的任意的试错。他说，后者的行为就“犹如同那些漫无目的地敲击键盘的猴子”，不具有任何智能，只能称之为一种机遇罢了［80］。

对BACON系统发现过程的细节考察使我们认为，BACON的方法确实具有培根方法的特征。孔宪中对BACON的评述，有值得商榷的地方。

孔宪中分析，BACON．1在重新发现开普勒行星运动第三定律（表达式为D3/P2＝c，即一个行星距太阳的距离D的立方被行星的周期P的平方所除，其值为一常数。）时，面对所给D和P数值，试图发现任意的常数函数关系，在启发式指导下，从最简单的乘积函数关系开始，BACON．1被限制尝试一组D和P的关系，从简单到复杂依次是DP，D/P，P/D，D2/P，P/D2，P2/D，D/P2……等，直到它试到第十四个假说即D3/P2，发现它与数据吻合，于是停止试错，将D3/P2当作经受了检验的假说接受下来。

我们说孔宪中的分析失之偏颇，首先在于他仅以BACON．1为BACON系统的代表，我们知道，BACON．1是BACON系统最原始的版本，它的发现功能及它的启发式相比后来版本还是很不成熟的。BACON系统的开发者认为，较成熟、完整和具有逻辑一致性的是BACON．3、BACON．4和BACON．5，因此他们以及别的科学哲学研究者一般都以这三个版本的启发式和发现过程为代表来评价整个BACON系统。

其次我们的考察表明，即便是BACON．1也不是用孔宪中描述的方法搜索函数关系的。因为从BACON．1开始就具有了最基本的三个探测数据规律的启发式：（1）递增；（2）递减和（3）常量，这在前面已经讨论过。所以，根据这三个基本启发式以及其它的丰富启发式的指引，BACON系统发现函数关系的过程是这样的：

以BACON．3再发现开普勒行星运动第三定律为例。在第一层数据中，BACON．3探测到随距离D增加，斜率S（即1/P）值减小，于是A递减启发式指引BACON．3定义乘积DS。BACON．3考察DS值，发现不是常量。这时，系统启动第二组发现规律启发式组中的一个产生式规则，将DS作为第二层数据中的一个变量，考察它与D的关系。于是，递归地运用A递减启发式及相应规则，定义新的理论词项D2S（即D2/P），考察D2S与DS的关系，由A递减启发式，定义D3S2（即D3/P2）这个理论词项，该术语被发现为常量，于是启动C常量启发式创建第三层次描述簇，在其中D3S2取定值。

由此可见，在发现D3S2＝c这个关系过程中，BACON并不是如孔宪中认为的那样，盲目地从简单函数关系到复杂函数关系逐个实验。而是在启发式指引下，初步类似人的智力那样高度选择性地或者说“聪明地”快速逼近那个最终结果。BACON设计者兰利等人的原话说得更明确：“BACON不做那类不加任何限制的、尝试一切的归纳，因为我们的研究目标是理解在系统考察过人们通过智能选择了少量可能性之后，那些不容易做的归纳究竟是如何完成的。BACON的搜索是高度选择性的，受几个强有力的启发式的指引［5］。”

正是因为BACON的数据驱动特征，BACON的发现过程真正实现了培根的理想，即不带有任何猜想、假设的完全由实验数据驱动的逐级机械式归纳。

培根方法的反对者、提出猜想－反驳方法的波普尔认为培根说的“interpretatio naturae”意指仔细琢磨大自然之书［99］。波普尔对培根这一思想的批判性诠释却抓住了培根归纳方法的精髓，并在此处与BACON方法产生了共鸣：BACON正是按照培根的方法在阅读大自然（得出描述性定律），而不是诠释大自然（得出解释性定律）。因为BACON仅限于发现经验定律，而且BACON发现的经验定律正是培根所提倡的可直接验证的知识，不带有猜想成分的确实的知识。

BACON实现的是培根的科学研究方法的第三步，归纳。而培根方法的第一步收集数据，和第二步整理数据，对于BACON来说都是由程序员完成的。我们通常说的指导人们进行观察实验的理论或猜想，都是渗透在培根方法的前两个步骤当中。而我们同样认为，培根科学方法的前两步如果没有理论性或常识性的知识和经验的作用不可能完成，培根试图不受任何“先入之见”的影响，去收集足够充分和好的数据只是他的一个理想。即使在拥有了搜索速度和搜索量已经远远超乎人们想象的计算机技术的今天，西蒙他们也依然不主张培根式的、“撒网捕捞数据”式的搜集事实。

3．BACON检验分析命题/综合命题的区分

兰利等人的论文中也讨论了BACON所引发的科学哲学和科学史方面的思考。BACON受数据驱动在重新发现经验定律中取得了成就，经验定律的发现在科学史上往往发生在科学家掌握很多某专业领域知识之前，即一个学科创立的早期。所以，兰利清醒地考虑到用这种培根方法所能发现的定律是有一定范围的［4］。而在科学史和科学哲学研究者中，也有一种很一般性的看法，认为归纳方法发现简单定律，演绎方法发现复杂定律。BACON也许可以作为这个规律的一个实验检验。但当我们仔细剖析BACON的发现方法之后看到，BACON还与一个科学哲学的重要理论问题的争议有关系。

科学哲学中一直存在着是否应该有经验性定律/解释性定律，或者观察命题/理论命题的划分。对于这种划分，早期的有力倡导者是休谟（David Hume，1711～1776）。休谟将知识分为两类：关于观念关系的知识（是分析命题）和关于事实的知识（是综合命题）。20世纪初兴起的逻辑经验主义运动接受休谟的区分提出：一切命题或者是先天的分析命题，或者是后天的综合命题，除此之外的命题都是不能证实或确证的因而是无意义的命题，所以应该拒斥形而上学。休谟的思想还可以追溯到英国的唯名论哲学家威廉·奥康（William Ockham，约1285～1349），后者将知识分为自明知识和证据知识，并认为只有这两类知识才能算作知识。可见，关于分析陈述和综合陈述之分在哲学家的知识论主张中，长时间居于毋庸置疑的地位，“从罗素、维特根斯坦、逻辑实证主义者到普通语言哲学家，都信守不渝，而尤以逻辑实证主义者鼓吹最力［100］。”

与此同时，对这种知识论主张的批评也一直没有间断。其中一个最有力的批评来自威拉德·奎因，一位具有实用主义倾向的美国分析哲学家。他批评这种划分来自于“经验论的两个教条”：其一是相信在分析的、或以意义为根据而不依赖于事实的真理与综合的、或以事实为根据的真理之间有根本的区别。另一个教条是还原论，相信每一个有意义的陈述都等值于某种以指称直接经验的名词为基础的逻辑构造［101］。奎因用他的整体论（Holism）的知识观论证这两种教条都是错的，分析和综合命题的区分不是绝对而是相对的，一切科学命题“只是在促使我们同感觉经验打交道的进展程度上有差别”。

奎因进行上述批判的靶子是逻辑经验主义。另一位科学哲学家波普尔也曾批评逻辑经验主义的两种语言观是错误的，在“观察名词”和理论名词之间的区别不成立，因为一切名词都或多或少地是理论性的，一切陈述也就都具有理论或假说的性质［84］。

两位科学哲学家对两种命题的区分的批判态度同样鲜明，不过在批判的哲学基调上有微妙差别：奎因立足于经验论认为一切命题都具有经验的成分，并提出他的“没有教条的经验论”，或者说整体论经验论。而波普尔则着眼于理性主义，从一切命题都具有的理论性成分来批评，以此也维护他的批判理性主义哲学。

70年代末，意大利科学哲学研究者佩拉从论证归纳方法对科学发现的重要作用方面，批评了区分规律的发现与理论的发现是“无根据的二元论”［102］。他批评许多哲学家由于这个二元划分得出的“经验定律可以借助于归纳发现，而理论定律则需要借助假说来发现”主张是一种“有限归纳论”。持有这种观点的哲学家从19世纪英国哲学家密尔（J．S．Mill，1806～1873，旧译“穆勒”），到20世纪的哲学家冯赖特（G．H．Von Wright）、戴（J．P．Day）、邦格（Mario Bunge）和卡尔纳普。尤其是逻 辑经验论者卡尔纳普的立场最具有代表性，他在“物理学的哲学基础”中写道：

理论定律比经验定律更加概括。然而，了解这样一点很重要：理论定律不能简单地从经验定律中得到，而需要更进一步的推广。一个物理学家是怎样获得经验定律的呢？他观察了自然界中某些事件，注意到某种规律性，用归纳概括的方法表述了这种规律性（Carnap，1966，‘Philosophical Foundations of Physics’，in：ed．by Martin Garner：228。转引自参考文献［102］）。

如何发现理论定律呢？我们不能认为“收集越来越多的资料，经过概括超过经验定律而达到理论定律。”理论定律不是用这种方法发现的。我们观察石头、树和花，看到各种规律性，并且能用经验定律描述它们。但是，无论

对这些东西观察的时间多么长，多么细致，我们也从来不能达到观察到一个分子的程度。“分子”这个术语决不是出自一个观察的结果。因此，观察的概括量再大，也不能产生分子过程的理论。这种理论必须用另一种方法产生。也就是说，它不是作为一个归纳事实的陈述，而是作为一个假说来陈述（同前转引自参考文献［102］）。

卡尔纳普的这种“有限归纳论”主张也是20世纪以来大多数归纳论者的立场。但是佩拉坚持一种反对“有限归纳论”的完全的归纳主义。他在论证了反归纳论者所坚持的假说－演绎方法具有两个谬误之后，对有限归纳论者在观察陈述和不可观察陈述之间的区分进行了驳斥。他认为两种陈述没有明确的分界线，实际上一切陈述只是在包含证据的程度上有差别。因此，归纳适用于一切科学发现，但是并不是说“每一次归纳的难易程度都相同”。

从奎因、波普尔到佩拉等等研究者，虽然一致反对观察陈述/理论陈述之间的区分，但他们对归纳方法在科学研究中作用的看法却大相迥异，而那些赞成这个区分的研究者中，他们对归纳方法的看法也存在明显分歧。看来，两种区分和归纳方法之间没有必然联系。实际也是如此，两种区分本身就是一个认识论的关键问题，关于它的争论具有重要的哲学意义。

我们这里讨论的BACON系统，它的技术细节无意中竟然向我们展示出它对这一争论的“参与”。前面，我们在讨论BACON系统各个版本取得的成就时分析道，BACON．1和BACON．2严格区分实验测得的数据与程序得出的假设却拓展能力不强，而BACON．3取消数据和假设之间的严格区别，却发现了更多的经验定律。BACON系统的实验结果告诉我们，突破以往MD程序对数据和假说（理论词项）之间的界线，能够更有效地做出发现。在人们对科学发现方面的方法论和认识论问题争论不休的时候，机器发现程序通过实验演示双方理论的实际效果，无疑对科学哲学理论起到检验的作用。可能人们还要对这种实验的结果做各种各样的解释，但是，它对我们研究科学发现以及其它科学哲学问题具有特殊的作用是毋庸置疑的。正像西蒙所说的，每一个MD程序不仅提出了一种科学发现的理论，而且它还实际演示了这个理论——这正是科学哲学研究应当重视的这种研究科学发现的新途径、一种计算途径的特殊贡献。

第2节　能否从波普尔思想中找寻发现的逻辑

前面我们分析BACON的方法中体现出培根的归纳思想，那么BACON或者说MD程序中究竟有没有波普尔的思想呢？有学者考察出，这两种一直被公认是截然对立的方法论思想，在当代的AI工作中被归并，或者说融合在一起。本节我们先来考察一下近年来科学哲学的成果中，如何重新比较培根方法和波普尔方法。进而，再通过对BACON所用产生式的细节分析，检验这种“归并”和“融合”。

1．一种误读——以波普尔的理论框架解读培根

人们曾经将培根和波普尔的观点视作完全对立的哲学学派。近些年，一些学者开始重新审视二人观点中的共性。英国科学哲学家乌尔巴赫（P．Urbach，也译为“厄尔巴赫”）曾撰文“作为波普尔前驱的培根”［103］，论证培根的科学方法论实际上正是波普尔的猜想－反驳方法的源头。人类的方法论史确实经常显现出这种循环往复、螺旋式发展的认识规律，但是，有一个也是人们试图尽量避免的现象，就是“矫枉过正”。

Sir Karl Popper（1902－1994）
图4－2　卡尔·波普尔
（图片来源：Stanford Encyclopedia of Philosophy plato．stanford．edu/entries/popper［2008－03－11］）

乌尔巴赫试图对培根思想提出一种与众不同的解释。他认为培根以证伪主义者的面貌出现，与波普尔非常相似。并且应当抛弃培根的那个“迷惑人的”主张：他已经发现了一种可以保障确定性的方法。

乌尔巴赫对培根思想的重新诠释，都是先陈述一般认为的观点，然后对这些一般观点进行反驳。这些对培根思想的一般性的或公认的解释有：

第一，培根哲学的中心思想是，在科学研究中可以通过一些纯机械的程序发现绝对真理。大多数著作家也因此认为培根哲学本质上是错误的。而作者认为，培根最有价值的观点是强调实验和猜测的经验证伪的重要性。

第二，通常培根的哲学经常被描述为与波普尔哲学正好对立。人们都认为培根反对思辩和假说方法。作者认为，事实上培根不反对带有思辩性的预测。而是反对拒绝在预测中使用经验证据反驳理论。因为培根哲学体系的中心思想是强调其方法的确实可靠性。

作者将培根的观点与波普尔的观点分别摘录出来进行比较，看起来的确是很相似。但是我们以为，这些相似都是在一些人所共识的观点上的相似，并不能说明他二人理论体系中核心思想的相似。

比如：作者举出的第一个相似点：培根认为“人的理智在本性上喜欢设想……，然而理智却为这些东西杜撰出一些本来不存在的和它们平行、成对和相对的东西”。类似地，波普尔认为“我们具有搜寻规律性，并把规律强加于自然界的倾向……，并企图在根本没有规律性可谈的地方去找到它们。”两个人的论述表明的其实是人们的一个共识，就是人类生来就有好奇心，就有探求自然界规律的强烈渴望。

第二个相似点：培根认为，人们总是喜欢为自己的观点想方设法找寻正面的例证，却忽视反面的例证；波普尔也说，人们倾向于把那些不支持他们愿望的事件当作某种“背景噪音”，舍不得放弃他们的期望。二人的观点还是表述了人们的一个共识，就是任何一个有理性的成熟的人都会有的坚持己见的举动。

下面，作者还举例说明，二人都认为人类理性中有一个认知的障碍，就是原有的思维定势使人们戴着有色眼镜认识世界，可能歪曲了事实。

作者还举例，培根认为“凡是以特别满意的心情详细研究的东西，都应当加以怀疑”，与波普尔的观点“在探索真理时，从批判我们最珍爱的信条开始”的相似性。可是，作者只注意使用词语上的相似性，却忽视了二人在“怀疑”和“批判”时所基于的根本信条是什么，恰恰二人在这方面截然不同，培根坚持用不含人的偏见的纯观察事实来怀疑。例如，培根在阐释他为什么说亚里士多德撰写的公认伟大的动物史并非是适当地探究过、证明过、衡量过的事物，培根提醒人们注意，“为作自然史而作的自然史与那种为对理解力提供消息以期建立哲学而集成的自然史是迥不相类的［98］”。而波普尔却认为要发挥人的想象力，大胆地提出具有高验证度的猜想去批判以往的理论。

作者甚至把二人将占星术等迷信活动作为科学对立面进行的批判，也当作二人观点相似的例证。可是，这仅仅是从培根以来的绝大多数科学哲学家都持有的观点。

总之，从作者举出的培根和波普尔的观点相似的“词句”中，无法有力地论证作者的观点：培根的思想是波普尔的猜想－反驳方法的源头。

但乌尔巴赫对培根的研究的确取得了一些重要成果，比如，对培根的猜测、排除等思想的再认识，这在一定程度上扭转了人们长期以来对培根思想的成见。而本文对发现逻辑的考察使我们不得不细心甄别出培根的猜测、排除方法与波普尔的差异。

我们理解培根思想中反对的是，不依赖完全的事实就进行的“冒测”。而一旦掌握完全的事实，他主张猜测！培根认为，在经过收集数据、整理数据以及对事实的三种表进行排除反面解释之后，就应该允许理解力“来做一回正面的解释自然的尝试”。他称这种尝试为“理解力的放纵”、“解释的开端”，或“初步的收获”［98］。可见，培根的“猜想”与波普尔的猜想不仅产生时间不同，而且产生的基础也不同。

另外，培根主张的排除是在他着手开始归纳普遍原理之前进行的，也就是在他的研究方法的第一步和第二步建立的三个表的基础上进行排除，在进行适当的拒绝和排除以后，一切轻率的看法都烟消云散，存留下来的将是一个肯定、坚固、真实而又定义明确的形式。培根指出，通过排除达到归纳出的规律的道路是曲折和复杂的［98］。所以培根主张的排除是伴随提出假说整个过程的，是事前的排除，而不同于波普尔的事后排除。

总之，作者的文章试图表明：在培根的理想中，科学应是由猜测和努力反驳构成的一个过程，这些猜测可以和真理相符，也可以不符。我们以为，这是作者先有波普尔的理论框架，再用之去解读培根，似乎是一种先入之见支配下的误读。虽然作者对培根的研究表现出以前为人们所忽视的培根思想的特征，但是作者未能有足够说服力地论证培根思想就是波普尔的猜想－反驳思想的源头。

2．波普尔与皮尔斯在发现理论上的比较

有学者将波普尔的思想与皮尔斯的思想做比较，得出结论，波普尔的证伪思想是来源于皮尔斯。对此我们结合本文讨论的发现的逻辑做一简要考察。

首先，他们的思想有一致的一面。皮尔斯提出，科学研究中是先提出猜想，由猜想再演绎出可能性的解释。这个程序中，皮尔斯以类似波普尔的猜想－反驳方法强调猜想。皮尔斯认为，面对纷繁复杂的自然现象，必须靠人类的一种天然倾向（能力），他称之为“猜测权（guessing right）”，直接提出关于现象事实的条理性的猜测。否则就不可能有现在如此大量的知识。另外人和动物一样，生来就有两类概念，一类是关于时空等的机械概念，一类是关于自己同类本质的种类学概念。前者产生出如静力学、动力学及其它物理科学（physical sciences），后者产生如道德、人类学之类的人文类科学。

类似地，波普尔也认为人类生来就有“知识”，虽然不是先天地正确，但是在心理学上或遗传学上是先天的，先于一切观察经验［99］。并且，波普尔在他的试错和除错，或者说猜想－反驳方法中，提倡“大胆地提出理论，竭尽我们所能表明它们的错误”，因为证伪度越高的理论才是越好的解释自然的理论。波普尔是在相同含义上谈理论和猜想的。在他看来，一切定律和理论本质上都是试探性、猜测性或假说性的。

但是，另一方面，他们的理论又有本质的差别。波普尔的猜想是尽可能多的、只要能想到的，也就是说，猜想的提出只受想象力这种心理因素的限制。而皮尔斯的猜想不是很多的，只是有选择性的几个。他提出有理性的选择标准，如，前提知识、实验检验等：

图4－3　皮尔斯
（图片来源：The Peirce Edition Project www．iupui．edu/～peirce［2008－03－11］）

对一个假说带有审问性质的第一次陈述，连同对假说的某种信任程度的接受，这些就是我所说的溯因法（abduction），一个推理性的步骤。……。如果不根据这两方面就肯定一个假说，这种做法是偏见，这两方面就是：第一，以带给该假说真理性的任何前提知识为基础；第二，对候选考察对象的诸多假说进行检验（Peirce，1957，Essays in the Philosophy of Science，V．Thomas，ed．，Bobbs Merrill，New York：236－7，转引自参考文献［17］）。(www.xing528.com)

然而，皮尔斯在提出上述选择可能性假说的理性标准的同时，又提出主要靠本能直接猜测出最具有似然性的猜想，他说，“通过似然性（by plausibility），我的意思是说，一个理论不靠任何证据而靠我们的本能，就能使我们相信的程度。……今天的物理学家在选择付诸检验的几个假说时，大大受这种似然性的影响［104］。”从这里，我们看到，皮尔斯的排除假说虽然有理性标准，但产生具有似然性假说却没有理性途径，只能靠本能的、直觉的猜测。所以，皮尔斯的发现理论是理性因素和非理性因素的综合，他承认发现有逻辑，因为排除不具有似然性假说就是使用理性准则，但他又不否认发现过程中也有心理学因素。对此，有研究者评述道，如果皮尔斯的所有对本能的提及，都用建立在知识、研究和背景理论的积累基础上的一种方法来代替，那么，他就对发现的逻辑有至关重要的贡献［17］。

其次，皮尔斯主张在发现的早期，要消除不具有似然性的猜想，这也类似波普尔的证伪思想。但是他们的观点仍有一个重要差别。波普尔所说的排除是在对已经完成的假说进行实验检验时才开始；皮尔斯的排除开始得早，发生在提出猜想的时候。这也由此导致二人之间的反对发现逻辑和提倡发现逻辑的根本分歧。

3．AI中既有培根方法也有波普尔方法

唐纳德·吉利斯（Donald Gillies）在《人工智能和科学方法》中，对培根的方法重新作了一番细致考察，也考察了培根方法与波普尔方法之间的分歧。人工智能尤其机器学习系统所取得的新进展，是促使他对这类传统科学哲学问题重新考察的积极动因。他得到了许多有意思的结论，比如他认为，培根的方法已经提出来有几个世纪了，但直到人工智能的出现，它才被真正运用，培根的方法论思想从机器学习研究的进展中已经得到了值得注意的辩护，而且其程度出人预料，事实上，培根的许多思想已经被编入那些成功的机器学习程序中了［18］。

但是吉利斯不赞同西蒙学派的机器发现途径，因为在他看来，西蒙他们太注重科学史案例分析，不如图灵传统的纯逻辑的AI途径成功。因此，吉利斯虽然有创见地认识到培根的归纳方法已经成为现代AI技术的组成部分，但是，他没有举出这方面的有说服力的AI实例。而我们前面对BACON程序的发现方法的考察有力地说明，培根方法在现代AI技术中得以实现。而且也表明，吉利斯全面否定西蒙小组的研究传统是片面的，尤其是他的否定并没有建立在对西蒙传统下的任何AI程序的案例分析基础上。而要重新阐释归纳主义和反归纳主义关于归纳方法的争论、要深刻理解AI程序与归纳方法的关系，再没有比深入考察一个声称是归纳主义的发现程序（BACON）更适合的了。

吉利斯的研究也认为，培根的归纳方法与波普的证伪方法并不象通常认为的那样截然不同，在这个观点上，吉利斯参考了乌尔巴赫的研究成果。他说：在一些观点上，两位哲学家走到了一起，如对证伪的重要性的认识。培根也强调证伪，并将证伪过程作为他的归纳方法的一个基本组成部分，“……真能得用的归纳法，必须以正当的排拒法和排除法来分析自然，……［98］。”吉利斯认为，不断被重复的猜想－反驳过程在所有的机器学习程序中都扮演了一个关键角色，但是与波普的猜想－反驳方法不同的一点是，计算机产生的这些猜想是一步一步地机械地由程序员设计的启发式给出的，而不是靠人的直觉。

我们认为，吉利斯对AI中使用的培根方法和波普尔方法的比较是恰当的。他的一些观点我们在前面的细节阐述中也进行了论证。而且，我们通过对BACON程序进行的较全面的案例分析，还将继续揭示两种方法在AI中的具体运用，比如，归纳、猜想、试错、证伪等等在机器发现中的特殊含义。

4．BACON方法是启发式的猜想－反驳方法

为了将BACON的方法与波普尔的猜想－反驳方法进行比较，这里，我们不得不详细引述BACON启发式的具体内容。

4．1　启发式蕴涵着猜想

我们以BACON．3为例，它的7组启发式由86条OPS2语言写成，具体的产生式组成如下：

1．收集数据：由17个产生式组成的第一组启发式负责收集直接可观察的数据。在这些产生式中，有7个负责收集来自使用者的对于这个被考虑的任务的信息。这种信息包括所有变量的名称，及其在系统控制下的建议值。一旦收集这些信息，剩余10个产生式就通过一个标准的析因设计收集数据。

首先，一个自变量的值被改变，保持别的变量值不变。第二步，增加第二个变量的值，从而第一个变量的各种值在这些条件下重新考虑。这样继续下去直到第二个变量的各种值都被生成。第三步，增加第三个变量的值，再进行一遍刚才的循环。用这种方式，自变量值的所有组合都被生成，观察每个组合的所有因变量的值。

2．发现规律：由16个产生式组成的第二组启发式负责记录下由第一组启发式收集的数据之中的规律，当追寻它们的目标时，这些规则能暂时中断数据收集产生式。系统的规律探测器可以分成一组不变性探测器和一组趋向性探测器。前者能处理符号和数值数据；通过形式化的概括和发现它们的条件，它们创造较高层次的描述簇。

BACON．3的不变性探测器是传统归纳推理规则的一个一般性版本，该规则可阐释为：

如果在L层的许多描述簇中

每一个因变量都有相同的值，

那么就在L＋1层中创建一个描述簇，在那里该变量取这个值。

随后启动发现条件的规则，该规则的简单表述为：

如果基于L层的许多描述簇

创建了L＋1层的一个描述簇

且一个因变量在所有较低层描述簇中具有相同值，

那么就将那个变量和它的值追加为新簇的一个条件。

BACON．3的趋向探测器只操作数值数据，其规则表述为：

如果L层的许多描述簇中

因变量V1随变量V2增大而增大，

那么就提出L层的V1和V2之间有一个单调增加关系，

并计算V1对V2的比值。

如果比值不恒定，就启动另一个规则，表述为：

如果L层的V1和V2变量间有一种增加关系，

并且V1对V2的比值不为常数，

并且导致这个发现的值都为正，

那么就假定一个新变量，V1/V2，在L层被定义。

计算理论值：一旦在一给定层次定义一个理论词项，就用另外3个产生式计算该术语在那个描述层的值。因为一个理论词项与一个特定描述层密切相关，所以只有相当量的工作已经在较低层被做了，一些术语的值才能得到。一旦这些值已经被计算出来，对规则探测器来说就是简单的游戏，去创建新层描述，或者更复杂的理论词项也会被定义。该结果来自这个事实，即被定义的术语同直接可观察变量之间是没有区别的。

3．注意多余的理论词项：在计算一个新理论词项值之前，BACON．3必须确信该术语并不等同一个已有概念。如果一个多余术语值被计算，那么可能探测到数学上有效但实验上无意义的关系（如，X/X＝1）。因此，由22个产生式构成的第四组启发式将新术语分解成它们最初的组成成分。如果对一个新变量的这个定义同一已有定义完全一样，该术语就被拒绝，而考虑其他的关系（或者，在一个线性关系中，该新术语被旧的代替）。

4．忽略差异：……，（比如在发现理想气体定律中）假定BACON．3已经定义了两个截距概念。第一个值是摩尔数＝1时的截距pv，t，1＝0，而第二个值是摩尔数＝2时的截距pv，t，2＝0。人们会期望BACON．3对这点作概括，阐述在所有的压力·体积与温度构成的线性关系中，截距都是0，而不论摩尔数为多少。但是，因为这两个截距是不同的术语，所以上面介绍的不变性探测器不可能应用。

BACON．3解决这个难题的方法是记录下两个截距仅是一个常数系数不同（设b为截距，pv与T构成的两个线性方程是：b＝pV－8．32T和b＝pV－16．64T），并定义这两个截距的抽象以忽略此差异。．．．．．与抽象术语相关的层次比产生术语的层次高一级；不必重新发现一已知的不变性，因此抽象术语的值被直接复制到较高层的描述簇中。一旦这些值被复制，规律探测器就能起作用；在此情况下，抽象术语的值总是0。

5．归并簇：当记录下一个不变性，就创建一个较高层描述，并且找出其成立条件。接着，如果在另一个变量上观察到一个不变性，就再定义一个簇。如果两个簇有完全相同的条件，它们就归并成一个单独的结构（即更高

层次的描述）；只有3个产生式能产生此过程。一旦这在许多簇对中发生，因变量值就能被比较，规律就会显现出来。

例如，假设BACON．3在不同地点做过单摆实验，并发现了伽俐略的单摆定律，P2/L＝K，在各处都适用。此方程中，P是单摆周期，L是支撑物的长度。但是，假定K值在不同地点不一样。现在，设想BACON．3在各处都挂一组物体，发现这组物体的加速度也随地点不同而各异。归并同一地点所获信息，就探测到一个规律。因为加速度随周期/长度的值的减少而增加，就考虑乘积加速度·周期2/长度；该理论词项值无论在何处都是一个常数。

6．处理不相关变量：再次考虑伽俐略的单摆定律，假定BACON．3从改变四个自变量的值开始——单摆长度，实验地点，悬挂物的重量，单摆相对垂直方向的初始角度。事实上，重量和角度（如果小值被检测）都与单摆周期没关系，但起初并不明显。

BACON．3用8个产生式构成的一组启发式来处理这种情况。这些产生式中最重要的是记录，一个变量值的描述层次比该变量被定义的层次高两级以上；这暗示最近变化的变量对因变量值无影响。……。这个产生式的效果是修正数据收集计划，不再改变不相关变量；将被考虑的值用于其余的运行过程。剩余的产生式执行这个过程的细节［4］。

从BACON程序的详细产生式中，我们看到，BACON程序的启发式中已经蕴涵了对可能数据模式的猜想和假设：常量关系或非常量关系。但这些猜想和假设与波普尔的猜想有差异。BACON的启发式都是指引程序寻找数据模式的规则，是数据驱动式的规则，而不是理论驱动式的规则，这些规则没有任何物理意义。从上述产生式中，我们也看到BACON没有被给予任何物理学或化学方面的背景知识。这同波普尔所说的通过创造性的直觉提出的解释性的假说或理论不一样。

但是应当看到，BACON只是机器发现程序中的一类，它完成复杂发现任务中的几项子任务，尤其是数据驱动发现规律的任务。而完成发现解释性定律的子任务的MD程序，如，DENDRAL、DALTON、PAULI、MECHEM等，都要被给予相应的化合物分子结构、粒子物理学等方面的理论知识。广义地从整个机器发现领域来说，MD程序的启发式中预置的猜想的确类似于波普尔的猜想，即对未来将发现的理论的设想。而且从AI技术整体来看，AI程序的运行过程似乎演示着猜想－反驳程序，对猜想进行着试错。但是AI程序中的猜想是受启发式制约的，其试错也是一种选择性试错，是在启发式规限了一定的搜索空间的选择性试错。简言之，AI程序的猜想由启发式产生，而波普尔的猜想完全归因于心理学或社会学因素。因此我们可以说，AI程序中具有的猜想－反驳方法，实际上是启发式猜想－反驳方法。

另一方面，AI程序的启发式搜索是限定了搜索空间，使程序更有效率地做出发现，但是也可能启发式起了误导作用，程序不能做出任何发现。那么，就重新修改启发式，设定新的搜索空间。人类的发现工作也是这样不能保证成功的探索性任务。这说明，BACON实验模拟了人类科学发现如何产生的主要特征。兰利和西蒙曾总结说，BACON采用的步骤非常类似于那些人类解决难题的研究中所出现的步骤，那些任务通常被描述成在可能方案的空间中进行选择性的启发式搜索的步骤。这样的步骤越少盲目性——也就是说，有更多现有理论知识来指导他，并使它从不适当的方向转过来——藏在实验数据中的规则也就能更容易、更直接地被发现［5］。

4．2　启发式蕴涵着可证伪性

AI程序与一般计算机程序的区别主要在于，前者以启发式解题策略为特征，而后者的解题策略是算法。从算法到启发式的策略转变，就增加了搜索结果的可证伪性。算法是精确地指明解决问题的步骤，如果一个问题有算法就肯定有解。而与启发式搜索相区别的尝试－错误搜索是尽量穷尽一切解决方案即算法，这些算法被形象化地表示为搜索树式的问题空间，这种方法可以说就是力求万无一失的“撒网捕捞数据”的方法，对计算机来说也叫“蛮力搜索”。逐一试错方法在不受搜索力资源限制条件下其证伪度为0。然而在现实的资源有限的搜索系统中，这是一种低效率方法。因此，AI的启发式方法虽然不能保证问题一定解决，但却常常是有效地解决问题的方法。

AI程序中的启发式策略虽然蕴涵了设计者期望的模式，但是要经受“手段－目的”分析的评价，不断为达到目标状态而修正局部状态或中间状态。就西蒙的机器发现研究而言，由于哥德尔定理以及前面分析过的算法信息理论中的定理，西蒙已经放弃了初创立AI领域时追求的通用问题求解目标，而致力于在确定领域中具有一般性的MD程序。所以，MD的启发式策略是指向特定目标的强方法。所用的启发式策略都是根据经验以及知识，具有高的先验概率的方法，这里就与波普尔追求的高的可证伪度相矛盾了。

例如，BACON的启发式是特别为搜寻特定类的经验定律而设计的。它在搜寻初等代数函数形式的经验定律时具有极低的可证伪度。但是，用BACON搜寻高等代数中复杂的函数形式，它就具有高的可证伪度。也表明BACON不适用于这种经验发现领域以及解释性理论的发现领域。可见，可证伪度在AI技术中不仅不是追求的假说的特征，反而是需要尽量避免的。实际的工程技术工作中应用的理论恰恰不是高可证伪度而是高的先验概率、尤其是高客观先验概率的理论。

另外，BACON的“条件－行动”产生式是用“IF－THEN”语句写成。这种语句是搜索树中的关节点，都是指向最后的假说的中间状态。但猜想－反驳程序是对一个已经提出的假说进行实验的确证或证伪。在猜想－反驳程序中已经无所谓搜索可言。搜索的任务已经完成。对一个已经提出的猜想的确证和反驳，都不指向下一步骤，它们不是中间状态，而是结果。

现在让我们再回到本章开头那个问题，我们也许应当改变提问的方式，比如改成：BACON是如何运用培根的归纳和波普的猜想－反驳方法的？

第3节　BACON是产生可能性假说的逻辑

现在，我们也许可以基于前面对BACON方法论问题的讨论，总结BACON的方法对科学发现逻辑的具体含义。首先，我们将70－80年代复兴科学发现逻辑的众多工作中，佩拉提出的“归纳主义”科学发现逻辑的模式进行补充，表示如下：

该模式将皮尔斯和汉森的发现逻辑中含糊的地方，用归纳主义的主张修补清楚。每一个研究者都身处于某种科学理论体系之中，加之他本人的其他知识积累以及信念，这些因素共同渗透在他的观察、实验活动中，这是汉森的“观察渗透理论”假说。但是，佩拉认为这时的理论是先前的已经被人们广泛接受的理论体系，而不是研究者提出的新的理论或假说（这是他与反归纳论者的区别之一）。新的假说是在最初的观察事实Oi（initial observations）的基础上，通过归纳方法提出来的。也就是皮尔斯和汉森提出的具有“似然性”的假说，即图中的Hp（plausible hypothesis）。但是在进一步用观察事实Oc（observational consequences）检验之后，将似然性假说修改完善提出最具有可能性的假说，可以称之为特定的假说Hc （certain hypothesis）。

实际上，佩拉是将皮尔斯和汉森的溯因法也作为归纳法，他对归纳法是一种广义的理解：只要是基于事实得出超出事实的结论的推理就称之为归纳，如他所说：

在我谈到“根据事实归纳”时，我指的是，那些前提为观察或事实报告的归纳论断，而不考虑这些论断的逻辑形式。换句话说，我不认为只有概括的形式或简单枚举的形式才是归纳。结论不是由逻辑的前提得出来的任何扩充性的论断也能称为归纳：只要这类论断起源于观察前提，而这些前提又描述了待解决问题的事实、情况或数据，那么，由此提出的解决问题的结论就是假说，并且这种归纳是一个“根据事实的归纳”［102］。

虽然佩拉和西蒙的工作的性质类似，都是试图强化或清晰化发现的逻辑途径。但是西蒙的归纳方法不能替代溯因法的存在，佩拉的广义归纳也不能忽视与归纳迥然不同的溯因法。我们认为，与其把发现的逻辑狭窄地限定在归纳逻辑，不如提出发现的逻辑是一种理性的发现方法，或者确切说，发现的逻辑是似然性的推理，其中包括像归纳、溯因、类比、分析、综合等多种推理形式，而AI技术已经表明，似然性推理是在启发式指引下进行的（Mercadal，1990：217）。因此，如果从事实到假说的具体推理形式不限于归纳，那么上面提出的科学发现逻辑模式就是我们认可的模式，它具有几个特征：（1）遵循从事实到假说的顺序，而不是相反。但这是一个不断根据事实排除错误的候选假说的过程；（2）是似然性推理形式；（3）推理受启发式指引，启发式的内容就是研究者的其它知识、信念和已有理论框架。

而BACON程序就是按照这种模式提出可能性假说的一个实例，具体说，它的启发式中没有理论框架，但有人类解题时使用的寻找数据模式的知识，而它的推理形式无疑是归纳。

另外，我们继续从贝叶斯定理中找寻发现逻辑的基础。贝叶斯定理的奠基者是18世纪数学家贝叶斯（Reverend Thomas Bayes，1702～1761）。自20世纪80年代前后，一批哲学家努力摆脱波普尔为归纳逻辑设计的那个“绝境”，他们采用贝叶斯证明的概率论定理，力图证明归纳命题的概率并不等于0。他们也被称为贝叶斯主义者（Bayesians）。贝叶斯定理规定了如何根据新的证据改变概率，其形式是［105］：

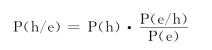
P（h/e）指根据证据e假说h的概率，P（e/h）指根据假说是正确的假定赋予证据e的概率，P（h）是不知道e时赋予h的概率，而P（e）是关于h的真值没有任何假定时赋予e的概率。由于P（h）是先验概率，是在考虑证据e以前赋予假说的概率，而P（h/e）是后验概率，在考虑证据e以后赋予假说的概率。因此这个公式告诉我们如何根据特定证据修改一个假说的概率。

由贝叶斯定理可知，如果假说一开始就不具有一定程度的可能性，无论观察结果的数量和质量如何，都不能认为它是成立的。简单的理解是，如果先验概率为0，则该假说的后验概率总为0。先验概率通过两种途径得到：一是利用过去的历史资料计算得到的概率，称为客观先验概率。二是凭借人的主观经验，或者说是主观信念来判断取得的概率，这被称为主观概率。大多数哲学家因为客观先验概率难以脱离普遍命题概率为0的“绝境”，而纷纷转向主观贝叶斯进路［105］。但是科学家并不如此，突出表现在，随着80年代以后兴起的机器学习和数据挖掘等AI领域的发展，贝叶斯理论得到广泛应用，有关的新的研究成果也层出不穷，贝叶斯理论的内涵已经发生了很大变化［106］。

按照反对发现逻辑的波普尔学派的观点，提出假说不是根据事实的推断，是完全非理性的、大胆的猜想，好的假说、具有更多经验内容的假说具有高的可证伪度（degree of falsification）或者说验证度（degree of corroboration）。但是，高的可证伪度等价的是低的逻辑概率，波普尔称这是一个真正值得注意的结果。根据他的观点，一个理论的可验证度C（g）与它的绝对逻辑概率P（g）之间可以是反比关系，即C（g）＝1/P（g）；也可以是互补关系，如，C（g）＝1－P（g）（参考文献［84］原书的注释［1］）。

那么由贝叶斯定理，这个具有很低的先验概率的猜想必然具有更低的后验概率，因此这个假说就不可能被确证，或者用波普尔的用语，被验证。如此，该猜想就应该如波普尔说的处于被证伪的境地。于是波普尔的证伪方法将陷入了一个逻辑“瘫痪”之中。

波普尔的证伪理论是在贝叶斯定理被广泛应用之前提出的，因此波普尔没有直接与贝叶斯主义者正面交锋，但是波普尔一定不会同意这种建立在归纳推理基础上对他的证伪理论的批判。因为，波普尔明确表示他的可检验性与逻辑概率是对立的，而他认为整个概率问题是被误解了的。我们不应该去讨论一个假说有多大的概率是确实可靠的，而应该努力评价它在多大程度上得到“验证”［84］。他还讽刺归纳逻辑追求高概率的策略，说，如果要赋予一个假说高概率，那么“最安全的方针是采取一个没有任何假说的系统。即言多必失，不说为佳。”

对贝叶斯定理的这番讨论，我们是想说明，按照哲学家的贝叶斯进路，归纳主义者如佩拉等对证伪主义批判的结果只能是双方各持一词、争论不下。不仅如此，客观贝叶斯进路也难逃波普尔的指责，而主观贝叶斯进路由于把概率的获得基于信念这类非理性因素，反而成为了反对发现逻辑的同路人。这里似乎又再现了皮尔斯的发现逻辑中，产生假说的“本能”说和筛选假说的理性之间的矛盾；也看到了汉森在提出假说上的“含糊其辞”。出路在哪里？我们以为还是应该回到贝叶斯技术本身。就如同AI领域中所做的，不抛弃客观进路，并且进行如西蒙的发现逻辑那样的技术处理，将先前的事实限定在一定区域内，如果在此区域内迄今有很高的概率，就可以据此提出似然性的假说，再根据后验概率修正可能的假说或提出新的可能的假说。

按照西蒙的发现逻辑，BACON程序所发现的定律只是为我们提出了最具有可能性的假说，它使用了基于归纳方法的理性途径。而BACON现在只能发现经验性定律，不能发现解释性定律，似乎表明支持有限归纳论的主张，但是继BACON以后相继开发的MD程序，已经有能够初步完成解释性定律的再发现，它们用的启发式是否还具有归纳特征，将留待我们以后进一步的考察。但是，BACON已经说明的就是，只有归纳方法对于发现可能性假说是不够的，发现的逻辑应该是包括归纳在内的多种方法，比如，兰利他们已经尝试在BACON的归纳方法基础上，增加类比启发式，就可能发现解释性定律［4］。