新途径：揭示科学发现的认知结构

第1章　研究科学发现的一种新途径

科学发现的认知建构，或者说创造性思维的实践研究大致有四个方面：计算机建模、神经网络建模、认知实验以及历史案例研究。我们的哲学考察选择计算机建模作为切入点，这是因为人工智能领域对科学发现的计算机建模密切结合了其他三个方面的成果。比如对发现程序的设计，需要以科学史考察得到的真实实验数据及科学家做出科学发现的真实过程作为设计的基础；而经过发现程序运行得出的科学发现思维的假设，还要经受以人为受试对象的认知实验的检验，根据检验结果调整发现策略的设计；同时，发现程序的开发和设计也运用了神经网络研究中的最新成果。本书的考察为避免泛泛而谈，选择了具体的发现程序BACON进行剖析，并且对其他主要发现程序KEKADA、PAULI、MECHEM等也进行了讨论。具体研究背景是这样的：

二十世纪最后二十年里，人工智能（AI）界出现了一个不同于历史、哲学、心理学的研究科学发现的新领域，即机器发现。这种机器发现工作已经远远超出了其本身所具有的人工智能价值，而对科学哲学、科学史乃至认知科学研究都产生了广泛影响。在众多机器发现程序中，BACON程序具有一定的典型意义：它重新发现的科学定律最多，是最重要的经验定律发现程序；它还是版本最多的机器发现系统；更重要的，BACON是西蒙（Herbert A．Simon，1916～2001）人工智能思想的成功范例。西蒙是人工智能的创始人之一，又是认知心理学的创始人之一，他在机器发现领域的探索活动同样是最早的。因此，从BACON这个西蒙传统典型机器发现程序入手，进行深入地案例研究，对考察科学发现的认知结构具有重要的方法论意义。

第1节　机器发现与BACON系统

1．机器发现：研究科学发现的新途径

科学发现是极富创造性的工作。人们相信，解读创造性之谜能帮助科学家更有效地做出科学发现。科学史家仔细分析一些著名科学家的手稿、信件以及实验室原始记录，试图“挖掘”出科学家做出科学发现的真实过程。心理学家从认知风格、创造人格及创造技法等独特角度研究科学发现。此外，还有做出科学发现的科学家本人对他的发现过程的回忆性描述。在种种研究科学发现的途径中哲学家的探讨是最早的。

对科学发现逻辑的探讨始自亚里士多德（Aristotle，公元前384～322）。自从亚里士多德的《后分析篇（Posterior Analytics）》以来，研究科学发现和形成概念的逻辑就是认识论的中心任务［1］。随着近代自然科学的诞生和发展，17、18世纪这项事业非常兴盛，科学发现的逻辑成为了许多大科学家和方法论家致力于解决的科学方法论的核心问题。其中代表人物有培根、笛卡儿、波义耳（Robert Boyle，1627～1691）、洛克、莱布尼兹和牛顿等。

但是，研究科学发现逻辑的事业在19世纪下半叶出现衰落。一方面，科学它的衰落与认识论上可错论（fallibilism）对不可错论正统地位的取代息息相关。另一方面，科学发现逻辑的研究被冷落一百多年，也与整个科学方法论研究的逐步势衰有关。从培根以降的方法论研究中形成的种种研究程序：归纳主义程序、猜想－反驳程序、常规科学（范式）→科学革命→新的常规科学（范式）的历史主义程序，以及科学研究纲领，由于都不具有普适性，费耶阿本德（Paul Feyerabend，1924～1994）就主张方法论的多元主义，反对有任何一种科学研究的普遍程序，从而使科学哲学中科学方法论的探讨陷入沉寂。在这种大背景下，科学发现方法论的研究就更加不是科学哲学家的兴趣所在了。

然而，大约在20世纪70年代前后，科学哲学界出现了一股复兴“发现的哲学”的潮流。这种复兴的“潜流”始自20世纪50年代汉森（Norwood Russell Hanson，1924～1967）对科学发现模式的研究，后来在20世纪70年代又有多位方法论研究者的努力，尤其必须提到的是以西蒙为代表的人工智能研究者对发现方法论的贡献。在对他们的工作进行剖析之前，必须先对西蒙学派研究工作中一个核心词语——启发式（Heuristics），稍作介绍。

“Heuristics”在计算机科学中译为启发式，也有其他领域学者译为“助发现法”、“启发力”。该词出自希腊语heuriskein，意思是“发现（to find）”。家喻户晓的阿基米德（Archimedes，约公元前287～212）发现浮力定律的故事中，那声著名的欢呼“尤里卡（eureka）！”，即是该词的一种形式。为了纪念这一事件，当今世界最著名的发明博览会还以“尤里卡”命名。关于heuristics的研究有时也用单数形式heuristic，但heuristics更常用，在这个意思上，该词与physics、mathmatics一样都作为单数使用。启发式这一概念，在20世纪中期，由于数学家波利亚（George Polya，1887～1985）的名著《怎样解题（How to Solve It）》而深入人心，在计算机科学、心理学、哲学以及法学等领域中都有运用。

根据维基百科（Wikipedia）的解释，启发式就是指人们在进行学习、发现或解题的过程中，能指挥人的注意力的一类重复有效的方法或途径。而在计算机科学中，启发式是指，为了简化难题使之容易解答而设计出的一类技术（technique）和经验规则（rules of thumb），虽然它们不保证最终解题方案的成功，但通常都会产生好的解题方案，或者可以解决一个涉及更复杂问题求解的相对简单的问题，但潜在地会损失精确性或精密度。

人工智能自诞生起就一直存在着以西蒙为代表的符号主义学派利用启发式搜索（heuristics search）技术探索人类思维过程的研究途径。他们使用计算机模拟手段探索人类解决问题的方法。尤其是20世纪70年代中叶以来，西蒙小组开辟了机器发现（Machine Discovery，简称MD）这个将AI技术结合科学史、科学哲学进行科学发现研究的新领域。该领域现在已做的工作主要是再发现，即开发计算机程序模拟科学史上重要科学发现的过程。

图1－1　1978年诺贝尔经济学奖获得者西蒙
（照片来源：nobelprize．org［2008－03－12］）

这种新的研究科学发现的途径为传统“发现的哲学”研究注入了活力。它不仅开拓了已有的科学发现研究的资源。机器发现还为我们提出了新的哲学问题并提供了新的研究手段。而且，面对众说纷纭的科学发现理论以及科学哲学理论，机器发现尝试使某些理论成为可检验的，这对科学哲学研究具有前所未有的意义。同时，这种新的研究途径能在多大程度上帮助人类揭开“创造性思维”之谜？它能否使科学史家、科学哲学家、认知科学家、创造心理学家甚至科学家本人对历史上科学家做出科学发现的过程有更多、更清晰的了解？这也是我们力图探讨的问题。

2．BACON系统的六个版本及其成就

以英国哲学家弗兰西斯·培根（Francis Bacon，1561～1626）命名的计算机程序系列BACON，是众多MD程序中最重要的经验定律发现程序。从1978年到1983年，先后发表了六种版本（BACON．1～BACON．6）。BACON的最早和最主要的开发者为P．兰利（Patrick W．Langley）。兰利1979年在卡内基－梅隆大学（Carnegie－Mellon）师从西蒙获得认知心理学博士学位。从BACON．4以后的版本是兰利与布拉德肖（Gary L．Bradshaw）、西蒙、席特考（Jan M．Zytkow，1944～2001）等人的合作研究成果。

图1－2　BACON程序的主要设计者兰利
（照片来源：www．isle．org/langley/discovery．html［2002－04－23］）

在这个研究团队中的布拉德肖，当时也在西蒙门下攻读心理学博士，他本科和硕士阶段都是心理学背景，现在是密西西比州立大学（Mississippi State University）心理学系教授。

来自波兰的访问学者席特考，既是AI专家，又具有深厚的科学哲学背景，曾获得华沙大学（The University of Warsaw）科学哲学博士学位。由于这种科学哲学背景，席特考成为了西蒙机器发现思想最热情和最坚定的实行者之一。他先后开发了FAHRENHEIT，49er，GALILEO，GELLMANN，STAHL，MENDEL等多个机器发现程序。他1982年开始加入西蒙的科学发现研究团队，跟随西蒙进行机器发现研究。20世纪90年代曾访问中国，中科院计算所的史忠植先生曾与他有过愉快的学术交流。但不幸的是，正当科学研究生涯的盛年，这位优秀的科学家却因病早逝，令人痛惜不已。在美国北卡罗来那大学（University of North Carolina at Charlotte）网站上，至今仍保留着席特考的纪念主页。

图1－3　布拉德肖
（照片来源：http：//www2．msstate．edu/～glb2［2008－03－12］）

BACON．1：科学再发现的初步实现

最早的系统BACON．1［2］能够解决序列外推任务，学习合取、析取概念，及发现简单形式的物理定律：如波义耳定律pV＝c（一给定量的气体，温度一定，其压强p与其体积V的乘积等于一个常数c）；开普勒（Johann Kepler，1571～1630）行星运动第三定律D3/P2＝c（一个行星距太阳距离D的立方与该行星的运行周期P的平方之比为一常数）。BACON．1是兰利博士论文的研究成果，它对通常发现系统的启发式进行创新，初步实现了“一个一般性发现系统”的设计初衷，可看作西蒙等人1974年提出的通用规则归结器的实现，但该系统只限于发现简单的幂函数。次年，兰利推出了第二个版本BACON．2。

图1－4　席特考纪念主页上的照片
（照片来源：席特考纪念主页coitweb．uncc．edu/～ras/Zytkow［2007－05－08］）

BACON．2：从简单到复杂

BACON．2将BACON．1的产生式加以扩展，增加了两种操作：一种用于在序列外推任务中发现递归模块，另一种用于产生多项式定律［3］。该程序通过检查数据的差异发现了复杂的多项式函数，例如，天文学中有名的经验定律，波得定律（Bode’s Law），该定律表明各行星环绕太阳的椭圆轨道的平均半径的数值之间是一种简单的数学级数关系。尽管BACON．2发现定律的复杂程度有明显提高，但根据该版本的启发式，系统不能被拓展发现更多的经验定律，而此技术问题在兰利接下来开发的BACON．3中有了很大的改观。

BACON．3：打破“观察”和“理论”的分界

BACON．3［4］是最成熟、最具逻辑一致性的版本，它成功地重新发现了理想气体定律、库仑定律、开普勒行星运动第三定律、欧姆定律和伽利略的单摆和匀加速定律。其成功的关键是取消了数据和假定的规律之间的界限：从低级描述层次中的数据概括出简单规律之后，就将此简单规律作为较高描述层次中的“数据”，由此“数据”再概括出更复杂的规律，这样逐级上升，启发式规则递归地运用于新的“数据”上，最后就可得出普遍性的经验定律。在这个过程中，系统描述层次逐级增加，更高的层次描述更复杂的定律，也说明了更多的原始数据，因此大大扩充了系统的表达能力。BACON．3的成功给了科学哲学研究一个启示，BACON．1和BACON．2严格区分实验测得的数据与程序得出的假设，却拓展能力不强，而BACON．3取消了数据和假设之间的严格区别，却发现了更多的经验定律。由此，我们熟悉的观察和理论的区别的争论在这里得到了一次生动的检验。

BACON．4：形成概念

从BACON．1到BACON．3，系统已经能够比较令人满意地完成科学发现过程的一个重要环节，即对数据进行分析，从数据中找出规律性的一个模式。但是，BACON系统能不能进行科学发现的另一个重要环节，形成概念呢？兰利同他的合作者对此进行尝试，结果在BACON．4中实现了这个功能。BACON．4［5］的改进之处在于增加了新的启发式，使系统能够规定出内在属性（如，导电性、比热等），从而使定律推导步骤简化为只需2个描述层次。而BACON．3在重新发现欧姆定律时，用了3个以上描述层次，而且为了描述电阻概念和电压概念，它将第三层次描述分成两个独立的描述簇（descriptive cluster），一个描述内部电阻概念，另一个对应于电压概念。这里的一个描述簇是关于相关变量值对（pairs）的一种猜测，如本章第二节中表1．1、表1．2中每行数据就对应一单独的描述簇。其中，为描述电压概念甚至用到第四层描述。稍后要谈及，比较发现过程的复杂程度时，所用描述层次数目也是一个评价指标。

BACON．4重新发现了阿基米德浮力定律、斯涅耳折射定律、动量守恒原理、万有引力定律、布莱克比热定律。但是我们应当清醒地看到，BACON只是发现了概念的数学表述形式。它根据启发式推理出这个数学表达式是有用的，而它实际上不可能知道该表达式具有什么样的理论意义。最终形成概念、赋予概念以理论意义都是人来完成的。可见，BACON发现经验定律的过程，是一个人机互动的过程。在这个人机交互过程中，人和机器各自发挥自己的所长，或者说，机器充当好助手与人一道更有效地做出科学发现。

后来兰利等人对BACON．4和BACON．5进行改进。因为在一些化学定量定律的发现中都有一个现象，一组值往往可以表达成其最小值的整数倍。于是，兰利等人引入一条新的寻找公因子的启发式（和已有的启发式合取），能够重新发现18世纪末至19世纪初的许多化学定量定律，如普劳特原子结构假说、道尔顿倍比定律、盖伊－吕萨克气体反应定律、杜隆－柏蒂原子热定律以及阿伏加德罗和康尼查罗原子量测定方法。

但是，兰利他们也清醒地认识到，BACON．4仅仅完成了对数据规律的描述，对所发现的公因子的解释还是由人完成的。因此他们寄希望于将来的BACON程序版本能从描述性定律的发现进入解释性定律的发现。

BACON．5：计算模拟优势凸显

在BACON．4和BACON．5重新发现布莱克比热定律时，还引入了一条对称性启发式，对称性规律在大多数场合是一个基本原理，这条启发式能省去大量搜索。但是这样一来，BACON就不是完全数据驱动而是具有理论驱动的性质了。为什么要这样做呢？因为科学史和科学哲学的考察已经表明，实际的科学发现过程既不完全是数据驱动也不完全是理论驱动，而是二者都起作用。兰利他们这样做具有多方面的意义。

第一，通过计算机模型的模拟恰好说明，数据驱动和理论驱动兼备的科学发现途径正是最有效的发现途径。

第二，BACON可以成为这样一种更普遍的科学发现模型，实验已经表明，如果数据驱动的发现系统BACON具备一种理论，就能使BACON的搜索空间减小，更有效地发现规律。

第三，BACON开创了一种研究科学发现的新途径，这种新途径具有传统研究途径无法比拟的优势。不论历史的、哲学的还是心理学的研究途径都不可能考察纯粹数据驱动或纯粹理论驱动的科学发现，因为这样的发现在历史上是不存在的。而通过计算机模拟，可以将启发式设计成完全数据性的或完全理论性的，从而分别考察数据驱动的发现模式或理论驱动的发现模式，利用新的研究手段就得出了新的研究结论，使我们对科学发现的本性有更多的了解。

第四，BACON以不同于人类的发现模式做出了相同的发现，BACON的实验表明，对于一个数据驱动的发现系统，非数据性质的启发式尽管很有用，却不是本质性的。因为BACON别的版本在没有该启发式的完全数据驱动下，通过更加冗繁的工作也发现了同样的定律。

BACON．6：发现复杂的多项式

BACON．6［6］是主要针对发现前述18世纪末至19世纪初的许多化学定量定律而改进的。它有能力处理大量的干扰，利用差分技术寻找相关的两变量之间最好的多项式函数，它能够发现像y3＝ax2＋bx＋c及sin（y）＝alog（x）＋b这样的关系。需要说明的是，BACON．6虽然是BACON系列中最后一个版本，但并不能说只有它是最成熟的版本，无论BACON的设计者还是评论者，都一致认为BACON．3是BACON系列中最成熟、最具逻辑一致性的版本，人们也都以它为例来评价BACON。

第2节　BACON系统的启发式及其运行特点

BACON系统作为一个成功的经验定律发现程序，它的启发式和运行特点很值得研究。

1．数据驱动及独特的启发式

1．1　数据驱动而非理论驱动

目前开发的机器发现系统大致有两类，理论驱动MD系统和数据驱动MD系统。理论驱动MD系统是指，将已知的抽象理论形式化后输入计算机，作为计算机已经知道的知识，设计启发式规则指导它的推理过程。这种理论驱动的MD系统适合在比较成熟、已经公理化的学科领域做出新的发现。比如，纯粹理论驱动的MD系统AM［7］，从约100个基本概念和约250个启发式开始，重新发现了数论中的概念并提出数学猜想。但是在自然科学中，即使像量子物理学这样抽象性、理论性程度颇高的领域，科学发现也不可能是完全理论驱动的。因此，BR－3［8］、BR－4［9］、GELL－MANN［10］、PAULI［11］等MD系统均是采取了理论驱动结合数据驱动，模拟量子物理学中的一些理论发现的。

数据驱动是给计算机输入经验性的知识，即纯粹定量的数据或者对观察实验的描述，并对探测数据规则的启发式进行利用。比如BACON，在给它输入历史上科学家做出真实发现的原始数据，以及探测数据规则的启发式之后，它就对数据进行分析，找出它们之间的相互关系，从中发现一种模式，这种模式表示了一系列数据的规律［12］。在它的发现过程中可以完全不需要任何专业理论知识背景。科学史上，尤其是在科学发展的早期，绝大多数科学发现都主要为数据驱动的过程，人们常常是先提出许多奇妙的纯粹经验性的定律、规则，而后若干年才能解释这些经验定律的理论意义。比如前面提到的波得定律、欧姆定律、孟德尔遗传定律等等。

属于数据驱动的经验发现系统还有函数归纳模型（Model of Function Induction），FAHRENHEIT，IDS［13］，GLAUBER、STAHL、DALTON［14］等。不同的是，最后三个系统所输入的数据是对观察结果的描述，而不是纯粹的定量数据。确切地说，DALTON还是一个数据驱动和理论驱动结合的系统。正如系统的命名所意味的，从GLAUBER、STAHL到DALTON，这三个系统分别模拟了在以经验性、直观性为主的近代化学发展史中的系列重要发现，如格劳伯（Johann Rudolph Glauber，1604～1670）对酸碱盐物质分类的贡献，斯塔尔（Georg Ernst Stahl，1660 ～1734）燃素说到拉瓦锡（Antoine－Laurent Lavoirer，1743～1794）氧化说的历史进程，以及道尔顿（John Dalton，1766～1844）推断物质的分子组成并得出原子量的过程。

1．2　启发式的特点

前面我们对启发式概念的含义作了初步介绍，通过考察西蒙学派的工作，我们还可以给出一个更简单明了的含义，启发式就是提高搜索效率的规则。BACON系统的启发式用OPS（Official Production System，通用产生式系统）写成。兰利认为该语言“为模拟人类行为提供了坚实的基础［4］。”这是一种著名的知识表示系统，它依据人类大脑记忆模式中各种知识块之间普遍存在的因果联系或“条件–行动”式，用“IF THEN”型的产生式规则来表示知识，以此可以方便、灵活地建立人类问题求解的认知模型。

兰利为BACON设计了丰富的启发式。以BACON．3为例，其启发式由86 条OPS2语言写成的产生式规则组成，这些产生式又被分成7个启发式组，分别完成不同的功能：第一组，收集数据；第二组，发现规律；第三组，计算理论项的值；第四组，注意冗余理论项；第五组，忽略差异；第六组，归并描述簇；第七组，处理无关变量。

因为BACON的数据驱动性质，它所运用的丰富启发式中，最基本的是三个探测数据规律的启发式：A．递增：如果X值随Y值的增加而增加，就定义比值X/Y，并考察这个值。B．递减：如果X值随Y值的增加而减少，就定义乘积XY，并考察这个值。C．常量：如果X的许多值几乎都是一个常量，就假设X总是取这个值。在启发式规则指导下，BACON的运行过程大致是这样的：

以一种系统方式收集数据，一次改变一个术语值并观察它的影响。如果一个变量值的改变没有产生任何影响，这个变量就是无关的而将它剔除。如果一个变量真的对另一个变量有影响，就定义一个新理论词项，该术语由自变量和因变量组合而成。如果以前没有考虑过这个术语的影响，就计算它的值并对其进行检验。如果这个术语的许多值都恒定，BACON．3就创建一个新的、更高层次的描述簇，并将这个描述簇视作该层次的数据。如果这个新的簇有完全相同的条件，这个簇可以与其他簇合并。若这个新术语的值不是常量，就再定义一个更复杂的术语，并重复上述过程。此外，对有用的理论词项和不变性的搜索在每层描述中重新进行一次。总之，这些启发式使得BACON．3成为一个强有力的而且一般性的发现系统［4］。

根据这三个基本启发式以及其他的丰富启发式的指引，西蒙评价说该程序的出色处就在于，通过这些步骤发现上述种种定律并不需大量搜索。很少需要考察原变量的12个以上的函数，就能找到一个不变量［15］。

1．3　BACON的发现过程

它的发现过程是这样的，程序先收集数据，然后根据数据表现出的趋向性和不变性定义理论词项。这些理论词项是对数据规律的简化描述，而且每个术语与一个特定描述层次相联系。BACON．3将数据和假说的区别模糊化，用了不同层次的描述。在BACON．3中，一个层次中的多个描述簇表现出的规律性能导致较高一层次的一个描述簇。进而这个较高层次的描述簇和它同层次的描述簇，又能导致更高一层次的描述簇。就通过这样的逐级概括，最终总结出能描述所有相关变量的相互关系和规律性的科学定律。

以BACON．3重新发现开普勒行星运动第三定律为例，分析具体发现步骤及启发式的运用。该定律表示一个行星距太阳的距离与行星运行周期之间的关系。其表达式为：D3/P2＝c。BACON是这样运行的，使BACON．3控制三个可观察变量（用到第一组启发式），分别是：原点对象、向量对象以及这两个对象被观察的时间。两个因变量是（用第一组启发式）：原点对象与向量对象之间的距离和行星的视差角度。

BACON．3开始收集数据（用第一组启发式），后两个变量随太阳系中不同的对象而不同。表1－1就是用上述方式收集的数据。

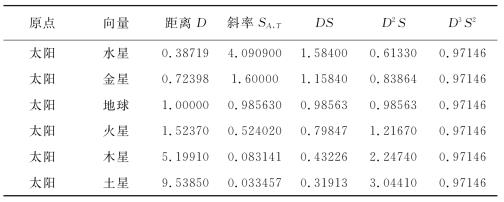
表1－1　关于太阳系的第一层次数据［4］

(www.xing528.com)

程序很快发现（用第二组启发式），在某些情况下，确定的距离值会重复出现。而出现这一结果的条件（用第二组启发式的发现条件规则）是以太阳为原点，太阳系中一个行星为向量。创建（用第二组启发式）第二层次的一组描述簇，用以描述这些规律。

相应地，BACON．3还注意到（用第二组启发式），随时间的增加，角度似乎也在增大。在每个选定向量的情况下，角度的斜率不随时间变化，是个常数。由此，定义（用第二组启发式）关于斜率和截距的线性关系理论词项，并分别用第三组、第四组启发式计算该理论词项值并考察它的唯一性。还需说明，定义的斜率和截距两个理论词项与为描述不同直线而创立的概念略有不同。结果描述簇表示在表1．2中。

表1－2　关于太阳系的第二层次描述［4］

接下来，BACON．3注意到（用第六组启发式）它有许多具有相同条件组的第二层次描述簇，但这些描述簇却得出了不同的概括。因此，它就废除（用第六组启发式）这些描述簇，而把斜率、截距和距离放在一起。接下来一步是将距离与角度对时间的斜率相联系。然而，每个斜率是一个不同的理论词项，在这种形式中，它们不能与距离作比较，于是转而进行下面步骤：

第一，BACON．3会认识到，这些概念定义仅仅区别在一个数值特征上，而既然它已经上升了一个描述层次，它也许可以忽略（用第五组启发式）这些差异而视这些术语相同。因为斜率值已经被计算出来，这个特征值就不再需要，因此，这个程序创立（用第五组启发式）一个新的，更抽象的角度对时间的斜率变量，并用这个新术语代替旧的术语。

第二，BACON．3有了它能检查的第二层数据，并且，它立即发现（用第二组启发式）在距离d和斜率s之间的单调递减关系。于是，一个新变量，ds被定义（用第二组启发式），并考虑它的值；现在，该系统注意到（用第二组启发式）ds和距离之间的一种递减关系，另外一个术语被创立（用第二组启发式），d2s，并再考虑它的值。然后另外一个关系被发现，术语d2s与ds也似乎是反比关系，于是定义它们的乘积d3s2为一个新的变量。BACON．3发现该术语有一个定值，于是创建第三层次的一个描述簇（用第二组启发式）；在考虑每一个向量对象时，都将太阳是原点对象作为关于这个规律的附加条件（用第二组启发式）。

第三，当BACON．3考虑不同的另一组对象，如木星和它的卫星时，这些对象很稳定地呈现这个规律。不用再重复过程，它只要计算（用第三组启发式）已有概念的值。再一次，理论词项d3s2被发现（用第二组启发式）是常数，但这一次它有不同的值。这些簇的共同特征是以木星为原点对象，这一点被加到一个新的第三层次描述簇中，作为条件（用第二组启发式）。注意s的值与行星运动周期p成反比，因此，d3s2＝0．97146是开普勒第三定律D3/P2＝c的另一种表示形式。

2．BACON系统的一般性特征

BACON系统已经重新发现了物理学、化学中的多个重要经验定律，作为AI中的一个计算发现系统，它的一般性程度如何是人们最关心的问题。程序的开发者和评论者曾部分讨论了BACON的一般性问题。尤其是兰利本人对BACON．3的工作做了定量评价。这些工作可以作为我们下面较为全面地讨论BACON系统一般性特征的基础。

2．1　所发现定律的表达形式具有多样性

BACON．3发现了5个经验定律，它们的表达式如表1－3所示。

表1－3　BACON．3发现的方程［4］

在理想气体方程中，n是气体的量（摩尔数），p是气体被施加的压强，V是气体体积，T是气体温度（开尔文温度），K1是一个常数。

在开普勒第三定律方程中，括号内部分是角度a与时间t组成的线性方程的斜率，是周期的倒数，d是行星（或卫星）距太阳（或中心体）的距离，K3是一个常数（0．97146，如前所述）。

在库仑定律方程中，F是两个小球（在扭秤中的）间的电引力，d是两小球间的初始距离，q1和q2为小球所带电荷，K4是一个常数（8．99×109牛顿米2/库仑2）。

在伽利略定律（单摆运动定律和匀加速定律）方程中，P是单摆周期；L是支撑物长度；d是一个物体被释放后所经过的距离；t是物体被释放所流逝的时间；K5是一个常数。

在欧姆定律方程中，T是被一根铜线轻轻触及的一根金属棒两端的温度，L是铜线长度，D是铜线直径，I是经过铜线的电流，K6和K7是常数。

BACON．3发现的这几个经验定律首先表现出在描述对象方面的多样性［16］42：从关于太阳系的定律，到对运动、气体、电等物理现象的描述。同时，还表现出算术表达式方面的多样性：从包含平方项或立方项的比值（开普勒第三定律，伽利略定律）到简单的乘积和比值关系（理想气体定律）。此外，BACON别的版本还能发现多项式形式的函数。

2．2　发现任务的复杂度比较

对BACON．3发现的五个定律其复杂程度的定量分析，可以作为进一步考察BACON系统能力适用范围的指标。定量分析的结果显示：欧姆定律的发现任务是这些发现任务中最复杂的。

首先，兰利比较了五个任务的相对复杂性。所用的测度方法如表1－4所示：

表1－4　五个任务的相对复杂性［4］

表中用了三个测度指标：启用产生式的数量、平均工作存储量、平均冲突组量。由表中数值我们看到，前2个指标，欧姆定律都排在各定律中的第一位，而且最高值和最低值相差近4倍；第三个指标，欧姆定律排在第二位，最高值和最低值间相差近1．5倍。综合考察表明，欧姆定律的发现任务在这五个发现任务中的复杂性程度相对最高。

接着比较五个任务的难度空间特征，该指标和前面指标一样，都表示完成任务时所调用的系统资源。从常识我们知道，一个任务越复杂，需要调用的系统资源就越多，机器发现任务也一样。兰利使用的测度方法如表1－5所示：

表1－5　五个任务的难度空间特征［4］

由表可见，五个测度指标，欧姆定律都排在第一位，例如：不仅所用的初始描述层次空间比大多数其它定律都复杂，使用的描述层次比其它定律都多；而且初始所用描述簇的数量是次高者的2倍，是最低者的3倍；还有，定义的术语数量是次高者的近2倍，是最低者的近3倍。这就意味着，欧姆定律的发现使用了更多的系统资源，因此是五个任务中最复杂的。

2．3　五个最一般性的产生式

兰利认为：“一个发现系统是一般性的，当且仅当它用的启发式是一般性的”。他总结出在BACON所有版本中，有一些产生式最具一般性。它们是：不变性和趋向性探测、析因实验设计、计算理论词项、注意多余理论词项、削减描述簇。这五个产生式分别属于第二组、第一组、第三组、第四组和第六组启发式。它们在上面五个发现任务中都起作用。而且在BACON系统的其它版本中也起作用。因此可以说，这些产生式是经验定律发现系统的一般性启发式的核心，这些产生式及启发式构成了BACON这一经验定律发现系统的一般性特征。在使BACON完成不同发现领域的任务时，只要在这些核心启发式基础上，增加指向特定领域的新启发式，就可使BACON发现更多的不同领域的经验定律。

2．4　可以不考虑实验顺序

另外，BACON．3系统的一般性还体现在它发现经验定律时能够经由不同实验观察顺序而达到的能力。兰利曾想：“如果不用考虑观察顺序，一个系统能发现同样的或等价的定律，那么该系统就是一个一般性的系统。”于是，兰利就对BACON．3进行这样的检验。结果，实验观察顺序的改变可能延长或缩短发现定律所用的时间，计算的复杂性（如所用产生式数量，工作存储空间）也受影响。但是，同样的经验定律还是被发现了，发现经验定律的结果并不受改变实验观察顺序的影响。

通过上面4个方面对BACON系统的一般性进行的考察，BACON已取得的成绩是，它在发现具有相当多样性的定律形式时，都共用了许多基本启发式，而且BACON可以在不考虑实验观察顺序的情况下做出发现。因此可以说，BACON是一个一般性的发现经验定律的系统，它能被很容易地扩展去发现更多别的形式的描述定律。

第3节　机器发现系统的研究价值

1．机器发现方法论研究的现状

BACON的出现引起国外科学哲学、科学知识社会学、认知科学等领域研究者的广泛关注。有的学者给BACON以高度评价，认为BACON程序是最出色的发现程序之一［17］。有的学者却对BACON给予断然的否定，认为BACON的工作以至于西蒙研究小组的这种研究途径是个失败［18］。有的学者对BACON的重新发现成就予以充分肯定，但对BACON能否从单纯发现描述性定律的机器系统发展为能发现解释性定律的机器系统持观望态度。也有学者强调BACON程序忽略了科学家实际研究工作中的某些重要特征，如时常参与科学家建构感知难题系统的信念、个人癖性等因素。除此之外，BACON也作为探讨创造性及科学发现的案例出现在科学哲学的教材中［19］，可见国外学术界对BACON给予的关注的广泛程度。

BACON也是引起SSK（即科学知识社会学）学者争议最多的一个机器发现系统。SSK学者发表观点的主要刊物，《科学的社会研究（Social Studies of Science）》，1989年第19期和1991年第21期皆专题讨论“计算机发现和科学知识社会学”，其中谈论最多的机器发现程序是BACON。从人工智能泰斗西蒙、著名人工智能哲学家博登（Margaret A．Boden），到SSK的领军人物科林斯（Harry M．Collins）、伍尔加（Steve Woolgar），以及认知科学学者萨伽德（Paul Thagard）等都参加了讨论。

与国外科学哲学界对BACON及其它机器发现系统给予的重视形成鲜明对照，国内科哲研究者对此关注不多，只有几位学者在他们的著作中简单提到过BACON或别的机器发现系统。周昌忠先生专论“科学发现的逻辑”［20］时，提到执行科学发现算法的“专家系统”BACON重新“发现”了若干重要物理定律。邱仁宗先生曾谈及［21］计算机科学的发展可为方法论或认识论的某些理论提供一个有效的检验手段，将BACON作为例子提及。章士嵘先生简要介绍过［22］BACON的基本设计思想及兰利对BACON存在问题的认识。王雨田先生和吴炳荣先生结合［23］归纳逻辑与计算机归纳学习的研究对建立新型机器归纳系统进行探索。他们的研究课题中将BACON作为能够成功实现观察学习，并通过材料驱动进行科学发现的主要AI系统实例，简要描述了BACON系统中的归纳推理过程。严湘桃等人在探讨［24］科学发现逻辑时，介绍了西蒙学派在人工智能方面的新进展，其中简要介绍了BACON系统的六个版本。

以上几位研究者分别从方法论史、科学哲学、认知科学以及逻辑学研究的视角，注意到BACON及其它机器发现系统的研究意义，但又都没有对机器发现及BACON系统进行深入系统的方法论和认识论分析。而迄今为止，国内科学哲学界即使是全面介绍BACON及机器发现系统的文章也鲜有见到，笔者只看到《科学与哲学（研究资料）》1985年第5辑有一篇译文，是兰利等人谈BACON和另外两篇发现系统的文章。以及《自然辩证法通讯》1983年第5、6期连载有一篇西蒙推荐的关于BACON的文章译文。上述现象也许说明，国内在人工智能和科学方法论之间关系的研究中存在盲点，介绍并参与80年代起国外科学哲学界对机器发现系统进行科学方法论研究的论文几乎没有。不过近几年北京大学科学和社会研究中心的硕士杨丽然、孟凡刚在任定成教授指导下的学位论文，相继对进行化学反应机理猜想的机器发现程序MECEM，以及做出粒子物理学新发现的机器发现程序PAULI进行了专门研究，可以说是国内该领域研究的有意义尝试。

当前，对机器发现进行广义的哲学视角（包括科学哲学、科学社会学、逻辑学、心理学，或者说认知科学）的考察已经成为国外方法论、认识论研究中新的生长点，是一个大有可为的研究领域。本论文在批判性地考察前人工作的基础上，首次对一个机器发现程序进行系统的、全面的方法论考察。本文以及前述两位硕士的工作填补了国内该领域研究的空白。而且，本论文从科学哲学视角考察西蒙AI研究中的科学发现思想，并分析机器发现领域的研究与科学哲学界复兴“发现的哲学”的关系，以及从科学发现观剖析人们对SSK理论的批评，这些方面的研究在国内都没有先例。同时，本论文立足于对BACON系统的技术细节考察，得出BACON对几个重要科学哲学理论有争论的检验结果，也是国内外还没有人做的工作。

2．机器发现是AI的专家系统范式向机器学习范式转换的关键

进行本书的方法论讨论之前，先明确BACON及其它机器发现程序的开发对AI研究的意义是很重要的，这对我们整个研究工作来说是一种必要的技术支持。但是，国内AI界迄今为止还没有关于机器发现领域的专著，这也与上面讨论的机器发现方法论研究呈现出国外热、国内冷的局面相对应。而国外关于该领域的比较有影响的专著，至少可以举出三部：1987年，兰利、西蒙、布拉德肖和席特考四人合著的《科学发现：对创造性过程的计算考察》，这本专著集中讨论了西蒙小组关于机器发现研究的诸多成果，被人们广泛引用；1990年，施拉格尔（J．Shrager）和兰利主编的《科学发现和理论形成的计算模型》，是斯坦福大学1989年召开的关于科学发现的计算途径研讨会的论文集；1997年，席特考主编的《机器发现》一书，汇集了机器发现领域几位主要研究者的论文，以及哲学家、实际工作的科学家对机器发现的观点。

因此，我们主要基于国外的AI研究，也参考国内的AI研究，对BACON系统的AI价值进行了定位。可以肯定的是，BACON系统受到了来自专家系统（Expert System，简称ES）、机器学习（Machine Learning，简称ML）、数据挖掘（Data Mining，简称DM）等相关研究领域的密切关注。机器学习的主要创始人、发明AQ算法的迈克尔斯基（Ryszard S．Michalski）与其他人合作，编写的有广泛影响的《机器学习——实现人工智能的途径》［25］一书，收录了兰利等人关于BACON．4的发现成就的论文。在迈克尔斯基等人编写的前书续篇《机器学习——实现人工智能的途径2》［26］425－469中，又收录了兰利等人全面评述BACON及其它经验发现计算机程序的论文。兰利等人关于BACON的研究论文还散见于《Science》、《Artifi－cial Intelligence》、《Cognitive Science》、《Machine Learning》等国际性权威学术刊物及AI专业刊物上。

国外AI研究者包括兰利本人，大多将BACON作为机器学习系统。对智能的研究使人们认识到，无论计算机“忠实地”执行了人们编写的多么复杂的程序，它的行为还是更体现出一种机械性而非智能性。从机械性行为的机器转变成智能性行为的机器，其关键在于具有“学习”能力。因此在AI领域，使计算机具有自发性地、能适应新环境和处理新问题的学习能力的机器学习研究已经成为最突出和最重要的一个分支。

人们已经开发出多种机器学习方法：从研究比较成熟的机械式学习（Rote learning）、讲授式学习（Learning from instruction）和再励学习（Reinforcement learning），到目前还处于探索阶段的类比学习（Learning by analogy）、归纳学习（Learning from induction）、观察发现式学习（Learning by observation and discovery），计算机系统对外界指导（Supervision）的依赖程度逐级降低，学习能力逐级增强。近年来还开发了基于神经网络的学习和遗传学习等新学习方法。其中发现学习可被看作没有外界指导的学习，它能根据实验数据或模型发现新的概念和定律，因而具有创新性，对实现机器自动获取知识的研究有重要价值。而BACON就是这样一个探索高层次机器学习系统的重要实例。

国内史忠植先生是迄今国内最全面关注过和研究过BACON及机器发现领域的AI科学家，他曾指导其学生于80年代后期进行过类似BACON系统的机器发现工作。《高级人工智能》［27］中，将BACON作为成功的知识发现和数据挖掘系统之一专门介绍。

数据库中的知识发现技术（Knowledge Discovery in Database，简称KDD）和数据挖掘技术于上世纪80年代末，在美国召开的国际人工智能联合会议（简称IJCAI）上首次提出后很快成为AI研究的热点。1995年开始，每年都要举办一次KDD国际会议。1997年，KDD还拥有了自己的杂志“Knowledge Discovery and Data Mining”。KDD研究于1999年达到了高峰，成为AI最活跃的研究领域。近两年KDD的研究虽有所降温，但与其密切相关的ML和DM仍然是AI的几大研究热点之一，目前国内很多大学和研究所也在进行KDD和DM方面课题的研究。由于ML、MD、KDD和DM的联系极为密切，是很难截然分开的研究领域，有学者将ML→MD→KDD作为KDD研究经历的三个发展阶段［28］。其实，无论机器学习、机器发现还是数据挖掘和知识发现都围绕着一个主题，就是知识。

四十多年人工智能发展的起起落落使AI研究者意识到，知识是关系到AI未来发展的核心问题。AI自50年代诞生后很快呈现出实用化的发展趋势。1965年问世了人类历史上第一个专家系统（Expert System，简称ES），DENDRAL。它用于根据有机化合物的分子式和质谱图判断分子结构。一般给出一个有机化合物分子式，往往有数千种可能的分子结构。该系统对于给定的有机化合物的分子式和质谱图，根据化学家关于质谱图以及其它化学知识，排除不可能结构，从几千种可能分子结构中挑选出一个正确的分子结构。由美国斯坦福大学的费根鲍姆（Edward A．Feigenbaum）领导的研究小组，包括化学家、遗传学家、AI科学家共同合作，经过从1965年到1983年的不断开发和完善，DENDRAL已经成为分子结构分析的重要手段，被用于学术研究和工业实验室，其成就可以与具体领域的化学家匹敌。

由于DENDRAL的过程包括发现和判断解释性的假说，所以也被看作是最早的发现程序之一［29］。DENDRAL的成功不仅标志着实用化ES领域的诞生，而且使ES领域成为AI研究的热点。随后人们相继开发出一系列应用在各个领域的专家系统。其中最成功的ES有：1972年到1974年开发的MYCIN医疗专家系统，1976年到1981年开发的用于地质勘探的专家系统PROSPECTOR。但是，经过ES十多年的研究，知识渐渐成为阻碍ES领域发展的突出“瓶颈”问题。1977年，费根鲍姆提出“知识工程”的概念，标志AI研究出现转折点：从实用性的获取智能的策略，变成了基于知识的方法研究。AI内部出现了从专家系统（ES）范式向机器学习（ML）范式的转换。80年代以来人们将AI研究的重点放在智能的基础——知识方面。知识表示、知识利用、知识获取成为AI的三大基本问题，史忠植先生2001年统计表明这方面的工作占据着AI研究的主流。

近年来，随着计算机网络和数据库技术的迅速发展，人们虽然可以建立越来越庞大的数据库、数据仓库，掌握越来越多的数据，而且数据增长的速度也在不断加快，可是人们却陷入“数据富有，知识贫乏”的尴尬境地。于是“数据挖掘和知识发现”这一新的交叉学科迅速崛起。AI科学家认为［30］，对于发现新知识来说，归纳永远是最基本的途径。因此，在以大量实际数据驱动来发现知识的研究成为主流的背景下，数据驱动的经验发现系统BACON的工作就具有重要的技术价值。从另一个角度讲，知识获取是AI技术曾经颇有应用前景的领域——专家系统之建造的瓶颈问题，专家系统应用性能的飞跃最终将依赖于自动知识获取即机器学习研究的突破。因此，BACON的主要开发者兰利的话清楚地表明了MD系统的研发对AI研究的意义：

人们对AI最主要的洞见之一就是，智能依赖于大量的专门领域知识。机器学习领域就关注获取那种知识的方法，而通往这个难题的途径之一就是机器发现［31］。

3．机器发现引发的科学发现问题

本书立足于讨论BACON引发的科学发现问题。这里既要考察BACON程序的开发者们对科学发现问题的方法论思考，也要考察其他领域学者，如，科学哲学、认知心理学、科学知识社会学学者围绕MD、尤其是BACON程序进行的关于科学发现问题的争论。

首先，BACON系统是西蒙人工智能思想的成功案例，通过考察BACON，我们将分析西蒙人工智能思想的特点，分析西蒙的科学发现理论，分析西蒙的信息加工心理学的AI主义认知心理学特征以及由此引发的对BACON工作的疑义。我们的考察表明，70年代以来的认知科学已经试图走出西蒙所创始的科学认知研究传统。

需要稍作说明的是，“Information Processing Psychology”国内心理学界通常译为“信息加工心理学”，如荆其诚、张厚粲翻译的《人类的认知：思维的信息加工理论》［12］等；而人工智能界通常译为“信息处理心理学”，如周少柏、黄汛翻译的《人工智能手册》［32］等。本文一般均使用心理学中约定俗成的称谓，但个别地方转述AI研究者的观点时使用了后一种翻译。

书中通过分析发生在计算论者和建构论者之间围绕BACON的争论，试图回答这场争论的焦点问题：科学发现是否完全独立于任何社会因素。考察中我们将对SSK学者关于科学发现的建构论主张进行细节地剖析。同时也考察一个不同以往的对SSK的批评视角。

在考察关于BACON的发现方法究竟是波普尔的猜想－反驳方法还是培根的归纳方法的争议中，我们的分析涉及到：西蒙的启发式搜索方法与试错方法的本质不同；AI程序与归纳方法的关系；以及证伪主义在AI设计思想中的具体体现。还有培根方法和波普尔方法之间的比较问题。并最终提出了我们认可的一种科学发现逻辑模式，而BACON程序就是具体实例之一。

除了上述BACON引发的科学哲学问题，我们还分析传统科学发现逻辑被抛弃的原因。并表明70年代以来关于科学发现逻辑的复兴计划已经在AI技术中实施。而BACON系统的设计思想吸取了发现哲学中的实证论、历史主义以及实用主义的“养料”，并结合AI技术总结了复兴科学发现逻辑的现代以实用性为特征的目标。

总之，本书试图系统地梳理BACON系统引发的科学发现方法论问题，并在历史地梳理论点当中发现争论的焦点。全书的研究方法是一种整合和分析相结合的方法，既将BACON引发的方法论问题进行整合式地讨论，又结合一个具体案例——BACON系统的启发式、产生式、所属AI学派及方法论基础等进行具有实质性内容的分析。