战略贸易政策：关税与补贴博弈之全球视角

第三节　关税与补贴博弈的比较静态学

这个关税和补贴的博弈模型结构，除了增加了政治决定的政府目标函数之外，和布兰德和斯班瑟模型（Brander＆Spencer，1984）是类似的。厂商之间在给定关税和补贴水平上采取古诺竞争，政府选择关税和补贴水平最大化其目标函数，均衡是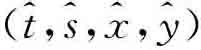。在给定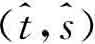）的情况下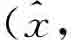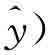，由古诺竞争最佳反应函数的交点确定。其中本国反应函数由π_y＝0得到y＝y（x，t，s），外国反应函数由＝0得到x＝x（y，t，s）。

命题1:由厂商最佳反应函数得到的最佳补贴和关税水平:

其中，y_t≠０，y_tx_s－y_sx_s≠０，δ≠１。

证明:

解上述方程组，得最佳补贴和关税。

但我们发现最佳关税和补贴的公式过于复杂，很难判断其变化的方向。也就是说，当厂商利益集团政治压力增加或消费者利益集团压力减小时，我们无法判断最佳关税和补贴水平是提高还是降低。

命题2:当不考虑关税政策时，由厂商最佳反应函数得到的最佳补贴水平:

证明:

在不考虑关税政策时，政府福利函数为:

G^δ（0，s）＝u（X）－pX＋δπ－sy

解方程，得最佳补贴水平。

两厂商进行古诺竞争的稳定性条件意味着

π_y＝p－c＋yp′＋s＝0

我们发现，当不考虑关税政策时，在δ＜1时，也就是利益集团利益不如消费者利益重要时，随着利益集团压力增加，政府补贴水平提高有利于政府总福利水平的提高。因为y_s＞0，p_s＜0，在δ＜1，所以有＾s＞0。

命题3:当不考虑补贴政策时，由厂商最佳反应函数得到的最佳关税水平:

证明:

当不考虑补贴政策时，政府福利函数为:

G^δ（t，0）＝u（X）－pX＋δπ＋tx

两厂商进行古诺竞争的稳定性条件意味着

π_y＝p－c＋yp′＝0

当厂商利益集团政治压力增加或消费者利益集团压力减小时，最佳关税水平提高。一个充分的条件是当δ≥1和p_t＜1。因为，机制的稳定性条件，x_t＜0，y_t＞0，所以。

为了分析问题的方便，以下我们只针对没有补贴政策的最佳关税水平进行分析，因为补贴政策的实施，首先是影响本国厂商的产量，进而影响外国厂商的产量，关税的存在首先是影响外国厂商的反应，再影响本国厂商的反应，两者的影响的结果是一样的^[3]。在不考虑补贴政策时，本国和外国厂商的利润函数分别为:(www.xing528.com)

本国厂商利润函数为:π＝yp（X）－cy－F　　　　　　　　　　　　　　　

外国厂商利润函数为:π^＊＝xp（X）－cx－tx－F^＊

政府目标函数为:G^δ（t）＝u（X）－pX＋δπ＋tx　　　　　　

命题4:厂商集团相对于消费者集团政治压力增加时，意味着最佳关税水平增加，即dt（δ）/dδ＞0。

证明:

对（3.5）式关于δ和t进行全微分，

现在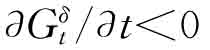，是政府福利最大化问题要求的二阶条件。这样，t_δ的符号与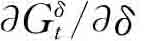以及［yp_t＋y_t（p－c）］的符号一致，都是正的，因为p_t＝p′Xt＞0和y_t＞0。

所以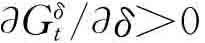，，并且，t_δ＞0。（证毕）

我们立即发现x_δ＜0（因为x_δ＝x_tt_δ和x_t＜0），y_δ＞0（因为y_δ＝y_tt_δ和y_t＞0），X_δ＜0（因为Xδ＝X_tt_δ和Xt＜0）以及p_δ＞0。这就是说，当代表厂商利益的政治压力增加时，产量增加，并且，外国出口产量由于一个更高的关税而减少。由于外国的产量的收缩仅有一部分由本国厂商增加生产，这样，随着提高的政治压力，本国消费减少，价格上升，消费者剩余减少。

由于本国厂商的产量和价格都是上升的，所以本国厂商利润上升。然而外国厂商经历一个出口数量的减少和价格的上升。假如我们考虑最佳关税的充分条件，价格相对于关税的上升是不大的，所以外国厂商利润是下降的。

命题5:厂商相对于消费者政治压力的增加，意味着本国厂商更高的利润，外国厂商更低的利润。

证明:

由本国厂商利润式（3.1）意味着π_δ＝y_δ（p－c）＋yp_δ＞0，因为y_δ＞0和p_δ＞0。由外国厂商利润式（3.2）意味着。现在，根据先前的条件，x_δ＜0，并且，由于最佳关税的充分条件，p_t＜1。这样，t_δ＞0，所以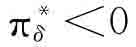。（证毕）

在厂商政治力量增强时，政府实施的关税增加，而本国厂商产出和利润增加。由于关税导致的利润转移的水平是δ的函数，δ测量厂商在选举中的重要程度。

下面考虑本国政治的角色:当δ＞1时，本国政治条件改变政府的目标函数，加大了厂商利润在目标函数中的重要程度。也就是说，当本国更多考虑进口竞争行业利益时，采取高关税，当更多考虑消费者利益时，采取低关税。或者说，当δ是低的，我们看到低关税；当δ是高的，我们看到的是高关税。

当δ＝1时，

最佳关税水平为布兰德和斯班瑟（Brander＆Spencer，1984a）关税。

从扭曲的贸易政策理论来看，在有垄断力量下，实行一个关税通常是最佳的。关税既能转移利润又能提高贸易条件。但是，当本国政府对本国产业利益考虑较少，选举利益更多来自于消费者剩余时，一个理性的政府往往会忽略利润转移而更多考虑消费者利益。这样，当δ足够低时，并且，1＞p_t＞x/（x＋y）时，自由贸易也许会是最佳政策。

推论1:假如1＞p_t＞x/（x＋y），Eδ∈（0，1）以至于＾t（δ）＝0。也就是说，对于足够小δ，自由贸易是最大化政府目标函数的最佳政策。

证明:

因为1＞p_t＞x/（x＋y），所以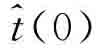）＝［x（1－p_t）－yp_t］/（－x_t）＜0。根据先前的条件，当1＞p_t和δ≥1时，t（δ）＞0。通过中间值定理，Eδ∈（0，1），因此，t（δ）＝0。