数据分析方法与实物期权技术投资评估研究

第四节　数据分析方法

一、Logistic回归模型

由于本研究的主要目的在于研究企业内外部各类不确定性对企业新技术投资决策的影响，而投资决策本身并非如经营绩效一样的连续变量，而是企业在特定不确定性环境下减少或不减少投资的决策选择，这种选择本质上可作为离散变量处理。在计量经济研究中，这种因变量是离散变量的模型称为离散选择模型（Discrete Choice Model），也被称为品质反应模型（Qualitative Response Model），是由表示选择项集合在连续变量和离散变量之间存在的差异而引起的。

离散选择模型通常都是在决策者效用最大化行为的假设下推导而来的，现有不同的离散选择模型就是通过对效用不可观测部分的随机误差项密度函数的不同设定而获得的，其中Logistic回归模型是使用最早并且最为广泛的离散选择模型，其因变量取值仅有0、1两种，也被称为二元选择模型（Binary－choice model），是本实证研究中采用的主要模型。下面简要介绍其基本原理。

当因变量的取值不是连续的，取值范围被限制在［0，1］时，普通的最小二乘法不再直接适用，而只能代之以最大似然估计方法（Maximum Likelihood Estimation，MLE）。模型参数的最大似然估计选择能够使函数值达到最大的参数估计值。换句话说，这套参数估计能够以最大概率再现样本观测数据。

我们首先写出以下的线性概率模型（LPM）：

Y_i＝α＋βX_i＋ε_i

其中，X_i是第i个个体特征的取值；Y_i取值为1或0，分别是两种选择下的赋值；ε_i是相互独立且均值为0的随机变量。

对上述方程取数学期望值，可将方程的左边转换成取值为0这一事件的发生概率，从而得到下面的方程：

p_i＝α＋βX_i

即解释变量的线性组合是线性概率模型中的一个概率值。

线性概率模型存在着很多的估算困难，比如，模型左边的取值在［0，1］区间，而模型右边的取值则不受此限制，因此一个自然的选择是对其进行一定的变换，使预测值对于所有的解释变量都落在（0，1）区间。

下面我们引入Logistic概率分布函数（Cumulative Logistic Probablity Function），Logistic函数也被称为生长曲线函数，其函数原型为

其中Z的取值区间为（－∞，＋∞）。

对上式我们做变换得

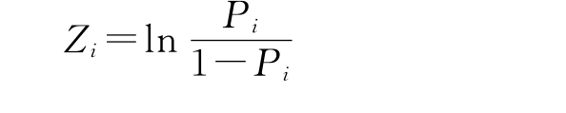
令Z_i＝α＋βX_i，得

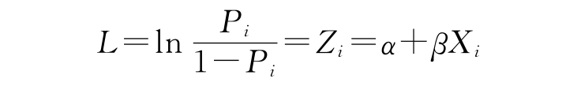
上述方程被称为Logistic方程，对应的

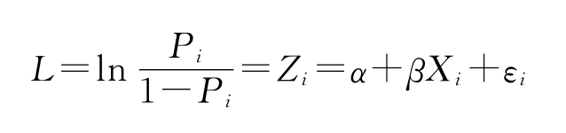
即为Logistic回归模型。

其更一般的形式为(www.xing528.com)

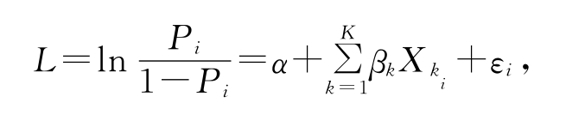
其中P_i＝P（Yi＝1｜x₁，x₂，□，xK），为在给定自变量x₁，x₂，□，xK的值时事件的发生概率。

利用Logistic模型，L的取值区间不再被限制在（0，1）区间，而是扩展到整个实数区间（－∞，＋∞）。并且L和解释变量之间是线性关系，因此，只要误差项满足经典假设就可以用OLS进行回归。但Logistic回归模型与OLS回归有不同的假设。第一，前面强调过，Logistic回归模型的因变量是二分变量，只能取0或1，研究的兴趣在于事件发生的条件概率；第二，Logistic回归模型中自变量与因变量之间的关系是非线性的；第三，在OLS回归中要假设同分布（Homoscedasticity）或方差不变，类似假设在Logistic回归模型中不需要；第四，Logitstic回归中也没有关于自变量分布的假设条件，各自变量可以是连续变量也可以是离散变量，还可以是虚拟变量。并且，也不需要假设它们之间存在多元正态分布（Multinormality）。但是，如果自变量之间存在多元正态分布关系，那么将能够增加模型的功效（Power），求解也能够提高稳定性（Tabachnick ＆Fidell，1996）。本研究采用SPSS15．0软件对Logistic回归模型进行参数估计。

二、调节作用检验与层次回归^[2]

（一）调节变量的定义与作用

调节变量的概念来自社会学与行为学研究，并逐渐在管理研究领域受到重视（Sharma，Durand ＆Gur－Arie，1981）。在管理学中，20世纪七八十年代发展起来的权变管理（Contingency Management）理论就是探索两个变量在不同情况下的关系，而代表这个“不同情况”的第三个变量，就是调节变量（Moderator），也叫条件变量（Conditional Variable）。调节变量可以是类别型或连续型变量，它影响自变量对因变量作用的大小或方向（Baron ＆Kenny，1986）。在线性回归或者实验分析范畴内，这种调节作用也常被叫做交互影响作用（Interaction Effect）。科恩等（Cohen et al．，2003）把交互影响定义为两个自变量通过交互作用对因变量产生影响且这种影响超过它们各自对因变量的影响之和。虽然调节作用与交互影响在数学分析上没有差异^[3]，但其名称的不同在于调节作用更强调调节变量本身具有的理论含义。在回归方程内，交互影响往往通过引入一个自变量与调节变量的乘积来表示，这样的回归分析叫做调节项多元回归（MMR，Moderated Multiple Regression）。

巴伦和肯尼（Baron ＆Kenny，1986）从概念上区分了两种不同的调节作用。第一种是一个自变量与因变量之间的相关系数会因调节变量的不同而变化，这种不同被称为合理性差异（Differential Validity）；第二种作用调节的是一个自变量与因变量的关系的性质，表现为相关性的正负方向会因调节变量的变化而变化，这种变化被叫做预测性差异（Differential Prediction）。有学者（Carte ＆Russel，2003）认为MMR只适用于预测性差异，但是没有指出具体原因。现在的主流研究似乎并不区分这两种不同。巴伦和肯尼（1986）的调节作用测试框架可以表示为图3—1。

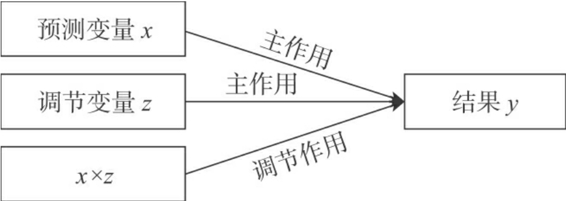
图3—1　调节作用示意图（Baron ＆Kenny，1986）

在这个框架中，预测变量x（以此命名，从而区别于调节变量）与调节变量z对y的直接作用叫做这两个变量的主作用（Main Effect），它们的乘积对y的影响叫做调节作用。如果调节作用显著，则调节作用假设就被支持。对于一个调节作用假设，主作用的显著与否并不是必要条件。

夏尔马、杜兰德和古阿里（Sharma，Durand ＆Gur－Arie，1981）专门根据前人的研究成果，就如何判断变量是否为调节变量以及调节变量的性质进行了讨论，指出：（1）如果一个变量与预测变量相关，且与预测变量没有相互作用，则该变量可能是一个干扰变量、外生变量或其他预测变量，要依其他性质而定；（2）如果变量与因变量和预测变量都不相关，且与预测变量没有相互作用，但根据此变量的高低来分组，如果在不同的组里预测变量的解释力会发生显著变化，则称这种变量为同质调节变量（Homologized Moderator），它会调节关系的强度；（3）如果变量与因变量或预测变量相关，且与预测变量相互作用，则称该变量为拟调节变量（Quasi Moderator）；（4）如果变量与因变量和预测变量都不相关，但与预测变量相互作用，则该变量为纯调节变量（Pure Moderator）。一般来说，对纯调节变量的回归系数有比较清晰的解释，对半调节变量的回归系数的理解必须谨慎。

（二）变量类型与回归系数分析

当研究中所涉及的变量（自变量、因变量和调节变量）都是直接可以观测的显变量（Observable Variable）时，调节效应的分析方法要根据变量的测量级别而定。一类是类别变量，包括定类和定序变量，另一类是连续变量，包括定距和定比变量。当定序变量的取值比较多且间隔比较均匀时，也可以近似作为连续变量处理。

以连续变量为例，下面给出最简单常用的调节模型：

＾Y＝aX＋bZ＋cXZ＋e（3．1）其中X与Z是中心化了的，XZ是中心化的X与中心化的Z的乘积，XZ本身没有中心化。这个方程表示在不同的Z取值上，有不同的Y与X的回归线，所以Y与X的关系是以M为条件的。对式（3．1）进行简单变换，有

＾Y＝（a＋cZ）X＋（bZ＋e）（3．2）（a＋cZ）是Y与Z之间的简单回归斜率，而这个斜率是以Z为条件的。对于该斜率的理解（即X对Y作用的强度）需十分谨慎。如果这些回归线在有意义的取值范围内互不相交，这时调节作用就是次序性的（Ordinal），否则是非次序性的（Disordinal）（Aiken ＆West，1991）。

此外，MMR的一个重要数学特征是它不具有尺度稳定性（Scale Invariant），也就是说，回归系数及其显著性会随测量尺度的变化而变化，这与没有调节作用项时的回归是不同的，所以需要对X和Z进行中心化处理。当一个MMR的回归系数可能会因为尺度的不同而改变正负时会误导对模型的理解，而且中心化的另外一个好处是降低多重共线性而不至于影响真正关系。当调节变量是类别变量时，通常会使用虚拟变量，必要时也可使用未加权编码或加权编码。当使用类别变量时，仍然可以对X进行中心化或标准化，但不需要对虚拟变量或其他编码进行标准化。

（三）层次回归分析

本研究主要用分层多元回归方法（Hierarchical Multiple Regression）来分析数据。我们可以有三个回归模型：第一个只包含预测变量的一次项，但也有学者（Frazier et al．，2004）认为这一步可以省略；第二个只包含预测变量与调节变量的一次项；第三个在一次项的基础上包含调节作用。但在实际处理中，存在步骤上是逐步向下还是逐步向上的选择。在逐步向下过程中，以一个包括调节作用的完整模型开始，然后去掉调节作用，最后去掉调节变量的一次项，而在逐步向上的过程中步骤则正好相反。就调节作用的显著性而言，我们只关注完整模型，所以采用哪个过程并没有差异。但当使用逐步向上过程时，可能会在做一阶项回归时被诱导去解释一次项的回归系数，但这时的解释是不应该的，因为还不知道调节作用是否显著。逐步向下的过程可以在一定程度上避免这种诱惑，所以效果可能更好（Aiken ＆West，1991）。我们不应该使用有调节作用却没有调节变量的主作用的模型（Cohen et al．，2003），因为如果一次项是显著的，那么对调节项的理解就会被这个忽视的一次项所混淆（Confounded）。对于调节变量的显著性，有的学者（Carte ＆Russel，2003）认为应该就这一项所增加的R²进行F检验，而不是直接对解释系数进行t检验。当一个调节变量调节多个预测变量时，或者当调节变量是虚拟变量时（这时有多个调节变量），显然，F检验是必需的。

测试后，对于＾Y＝aX＋bZ＋cXZ＋e，如果c不显著，是否要去除XZ并重新估计其他系数？艾肯和韦斯特（Aiken＆West，1991）认为这是由理论决定的。如果在理论中有很强的理由来认为有这样的调节作用，那么即使结果不显著也不要去重新估计，这有助于积累这个领域的发现，并为以后的宏观分析（Meta－Analysis）做铺垫。也可以尝试着去掉XZ来观看对系数a、b的影响，这时，这种观察是探索性的而不是实证性的。

根据阿诺德（Arnold，1982）以及夏尔马、杜兰德和古拉里等（1981）的描述，本研究对调节变量的具体操作如下。首先根据方程（3．1），做Y对X的回归，检验XZ的回归系数检验是否显著：若显著，则仅需判断Z是否与X或Y相关，若相关则Z为拟调节变量，若不相关则Z为纯调节变量；若XZ的回归系数检验不显著，则需要判断Z是否与X或Y相关，若相关则Z不是调节变量，而是其他变量（如外生变量、预测变量、干扰变量等），如果Z与因变量和预测变量都不相关，则将总样本根据Z的大小分成两组，检验不同组内预测变量的预测效度是否具有显著差别，若有差别，则Z是同质调节变量，影响关系强度，若没有显著差别，则Z不是调节变量。