中国省级GDP统计数据的内在矛盾及修正探讨

第六章　典型省GDP统计数据的内在矛盾及其修正

第一节　问题的提出

前面我们在对各种数据进行平稳性和协整性检验的基础之上，构建了模拟GDP的能源消费模型、自回归移动平均模型、基于非GDP核算变量模型以及模拟各次产业增加值的非GDP核算变量模型，并依据模拟的GDP及三次产业增加值，计算了相应的增长率。计算结果表明：

（1）以非GDP变量作为解释变量，模拟各产业增加值，再依据各产业增加值计算出各产业增加值的增长率，最后，求出各产业增加值增长率加权之和，得到GDP增长率。此方法得到的GDP增长率，明显高于统计增长率和按能源消费模型、ARMA模型以及非GDP核算变量模型计算的GDP增长率。这表明，各次产业增加值数据与GDP之间应有的内在关系被破坏了，说明GDP数据和各产业数据受到了人为的“污染”，因而失去数据间应有的内在关系。

（2）各种模型模拟的GDP序列具有较强的波动性，而且波动样式基本相同，而GDP统计增长率则更为平稳，表明GDP统计增长率存在着经过人为“加工”处理的可能性。

（3）各次产业增加值增长率的算术平均值与加权平均值以及依其他模型模拟的GDP计算的GDP增长率，具有非常相似的波动样式，而且并没有系统地低于统计增长率，这与GDP增长率的核算理论相矛盾。这表明，GDP增长率与各产业增加值增长率受了到扭曲性加工。

然而，上述只是根据各种模型模拟的增加值计算的增长率之间的关系，通过理论分析和对比分析得出的初步结论，或者说上述只是一种理论猜测。要证实这种理论猜测的正确性，必须要获得进一步的证据。

本书将以典型省2005年统计年鉴发布的数据为基准，探测数据的结构问题，并根据前面的模型，推测出关于GDP及其增长率的一组参考数据。

第二节　典型省GDP统计数据存在的内在矛盾

一、GDP核算的基础理论

为了理解和说明典型省统计数据间的不协调性，我们先从理论上说明一下GDP核算的基础方法及其性质。国民账户体系的GDP核算基于投入—产出技术。众所周知，依据投入—产出平衡表，可以用三种理论上完全等价的方法计算GDP：生产法、收入法和支出法。

生产法计算的是所有生产部门增加值的总和。在投入—产出表中表现为总产出扣除中间投入，即GDP =∑VA（增加值）=∑[GP（总产出）-IP（中间投入）]。

收入法计算的是支付给最初生产要素的全部报酬的总和。在投入—产出表中表现为正方形产业间转移矩阵底部的一个长方形矩阵。收入法GDP等于工资、利息、利润以及净税收等之和。用公式表示则为：GDP =∑[W（工资）+ IN（利息）+ P（利润）+ R（租金/使用费）+ IT（间接税）- S（补贴）]。

支出法计算的是社会最终消费的物品与服务的价值总和。在投入—产出表中表现为正方形产业间转移矩阵内右边的一个长方形矩阵。支出法计算的GDP用公式表示则为：GDP=∑[C（消费）+ I（投资）+G（政府购买）+X（出口）- M（进口）]。

如果社会中各经济活动主体能够提供生产过程的准确信息，并且上述各种核算方法中的每个环节的具体核算正确无误，那么上述三种方法核算的GDP应该是完全相同的。然而，由于实际经济过程非常复杂，核算GDP所涉及的各种变数经常变动，因此，即使核算方法正确，也不能保证上述三种核算方法核算出的GDP完全一致。Klein和Makino（2000）曾用不同方法对美国季度GDP进行核算，发现在支出法和收入法之间存在显著的差异，而且这一差异并不是一个随机序列。它不仅有一个相对稳定的变化模式，而且与其他经济变量高度相关。同样，支出法和生产法之间同样存在类似的差异。

到目前为止，中国主要采用生产法进行GDP核算，同时给出支出法核算的名义值，但中国各省按支出法计算的名义GDP实际上没有什么意义，大部分省份采用所谓的“剩余法”计算名义GDP，即利用生产法计算的GDP，减去政府消费、私人消费以及总投资，剩余部分即算做出口。

因此，本书分析的典型省GDP统计数据上的矛盾，不是指不同核算方法导致的矛盾，而是指利用生产法核算而导致的内部关系上的矛盾。

二、典型省GDP总量上存在的矛盾

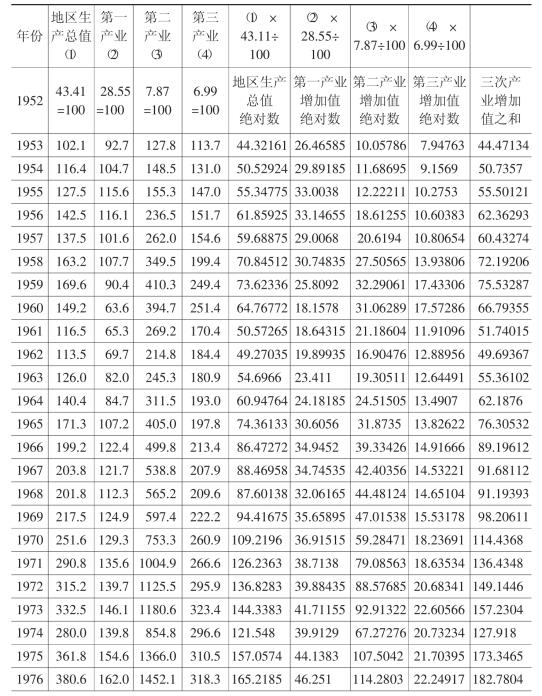
典型省各年的统计年鉴几乎都给出按两种不同方式计算的各年GDP：一是以1952年为100的各年GDP指数；二是以上一年为100的GDP指数。这两种方式计算的GDP，又都分别给出了不同产业增加值的指数。根据前面的理论说明，不论是以1952年为100，还是以上一年为100，GDP都应该等于三次产业增加值之和。然而，我们的计算结果表明，典型省各年的GDP却与三次产业增加值之和存在巨大差异。为了理解这种差异，我们按如下步骤分别计算了典型省GDP。

首先，典型省统计年鉴给出了以1952年为100的各年GDP指数。用各年GDP指数乘上1952年的基数，便可得到各年以1952年价格计的GDP绝对量。

其次，典型省统计年鉴给出了各年以1952年为100的不同产业增加值指数。因此，用各年不同产业增加值指数乘上各自的1952年的基数，便可得到各年不同产业增加值以1952年价格计的绝对量。

最后，将同一年的三次产业增加值相加，得到全部增加值，即理论上的GDP。表6-1给出了按上述方式计算的结果。

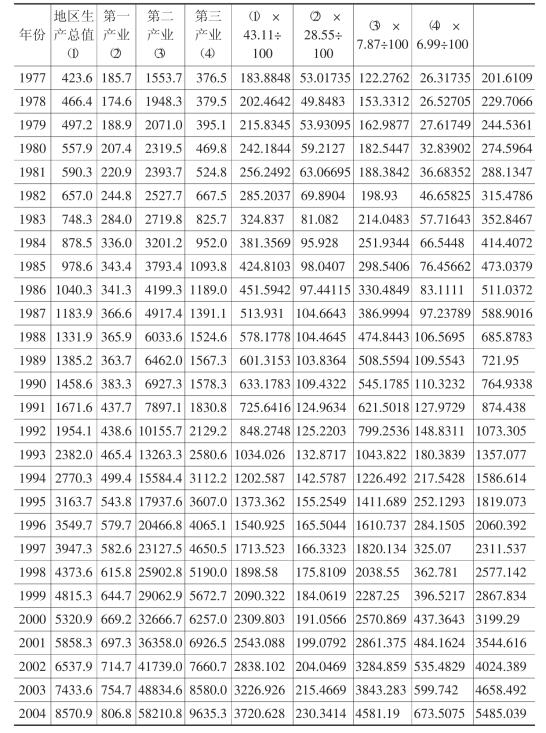
表6-1显示，按GDP指数计算的各年GDP绝对量显著地小于三次产业增加值之和，如果这种差别属于核算误差，那么核算误差总应该处在一个可令人接受的范围之内，并且应该是随机的。但情况并不是这样，实际上，这两者之间的差距越来越大。观察表6-1不难发现，20世纪50年代和60年代，平均每年相差大约2亿～3亿元；20世纪70年代平均每年大约相差10亿～20亿元；20世纪80年代平均每年大约相差30亿～100亿元；20世纪90年代平均每年相差大约100亿～700亿元；进入21世纪平均每年的差别则扩大到1000亿～1600亿元。显然，这种状况与GDP核算理论相矛盾。

表6-1　按地区生产总值统计指数和三次产业增加值统计指数计算的典型省总增加值

续表

三、GDP结构上存在矛盾

如果说GDP与三次产业增加值之和存在误差是正常情况的话，那么，无论是一个国家还是国家中的一个地区，其总增加值都应该大于各分产业增加值。然而，从表6-1中我们可以清楚地看出，从1993年开始，典型省第二产业增加值已经超过典型省GDP。据此，我们很难理解《2003年典型省国民经济和社会发展统计公报》（典型省统计局2004年2月26日发布，典型省统计信息网）所说的，“三次产业结构由上年的13.2∶50.3∶36.5调整变化为12.1∶53.5∶34.4，第一产业、第三产业比重分别下降1.1个百分点和2.1个百分点，第二产业上升3.2个百分点。”由于第二产业增加值已经超过了GDP，怎么还会有第二产业之外的产业存在呢？这种结构上的矛盾，如果不是数据受到了人为的“污染”，那么，就是统计方式上出现了问题。但如果是统计方式上出现了问题，那么，年复一年的统计年鉴，怎么会一直存在这种矛盾呢？此外，既然第二产业增加值已经超过了GDP，那么，上述的三次产业结构的比例关系又是依据什么计算出来的呢？

四、GDP增长速度上的矛盾

从理论上说，GDP增长速度应该等于各产业增加值增长速度的加权和，由于典型省GDP在结构上存在矛盾，因此，无须计算我们都能够断言，三次产业增加值增长速度的加权和一定远远大于GDP的统计增长速度。然而，问题却不仅如此，即使将三次产业增加值之和与GDP不相等看做是核算中存在的误差，那么，依据三次产业增加值之和计算的总增加值的增长速度，应该与GDP的增长速度相一致，但事实并非如此。表6-2给出了我们计算的结果。

表6-2　典型省GDP统计增长率与三次产业增加值之和增长率

表6-2中的数据表明，依据三次产业增加值之和计算的总增加值的增长速度与GDP的统计增长速度之间，自20世纪80年代中期之后除个别年份外，存在十分明显的差距。同时，绝大多数年份，GDP统计增长率小于按三次产业增加值之和计算的增长率。显然，要对增长速度上存在的这一矛盾做出恰当的解释，的确不是一件容易的事情。

典型省GDP统计数据存在的上述种种矛盾，不论源于什么原因，对于正确估计典型省经济发展水平和速度，都是极为不利的。正确地估算GDP，只是为了发现经济发展中存在的问题以及评估不同发展方式对经济发展的影响，以便做出正确的政策选择。为了修正典型省GDP统计数据中存在的种种矛盾，下面我们利用相关模型来重新构建典型省GDP序列。

第三节　典型省GDP数据的重新估计

前面我们利用各种不同的模型模拟了典型省GDP。根据模拟优度的理论评判准则，这些模型的模拟优度相当不错，大部分模型能够解释GDP或不同产业增加值变差的99.9%以上，同时，根据模拟误差的均方根、绝对值误差均值、绝对值百分比误差均值，Theil不等系数、偏差比率、方差比率以及协方差比率判断，这些模型均能够比较好地模拟GDP或增加值的波动样式。但由于这些模拟模型是约束下的回归模型，因此将不能被解释变量所解释但又与解释变量不相关的影响，归并到截距项中，因此，这些模型只适用于对GDP的模拟而不适用于对GDP的重新估计，但这些模型也为我们重新估计GDP提供了重要线索。

前面我们构造模型时，首先对各变量进行了平稳性和协整性检验。变量间存在协整关系，表明这些变量基本上协同运动，因此，我们利用前面的各种模型所提示出的这种协整关系，来重新估计GDP和各产业增加值并据此计算其增长率。

一、GDP及各产业增加值增长率序列的重新估计模型

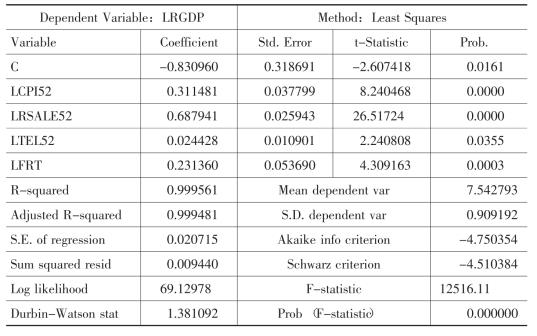
前面我们曾用下面的4个模型来模拟GDP及各产业增加值：

模型1GDP模拟模型

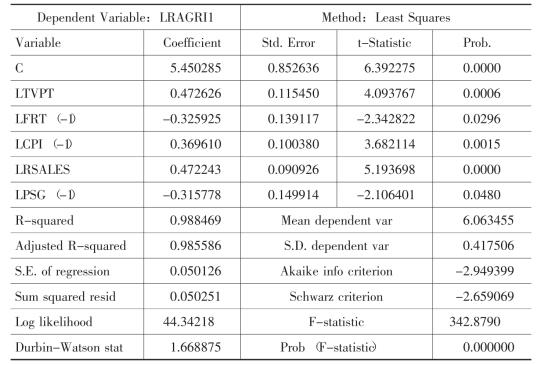
模型2　第一产业增加值模拟模型

模型3　第二产业增加值模拟模型

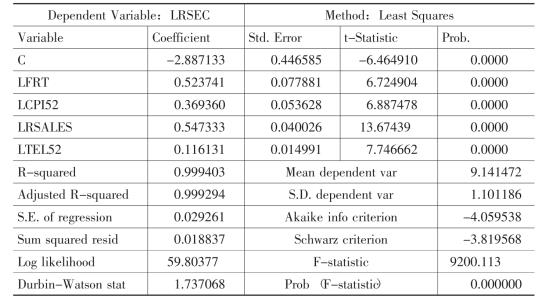
模型4　第三产业增加值模拟模型

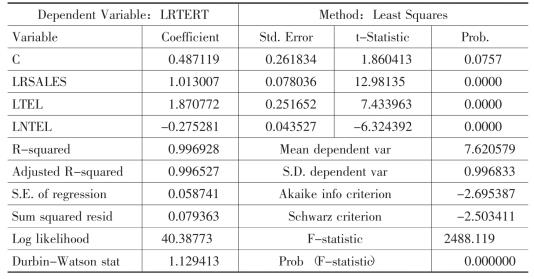
由于社会商品零售总额是经济是否景气的一个重要风向标，而且其在各个模型中都是统计上最为显著的变量，所以我们依据这4个模型所确定的GDP及各产业增加值与社会商品零售总额之间的关系，重新构建GDP及各产业增加值增长率序列。

上述4个模型分别表明，社会商品零售总额变化1个百分点，将导致GDP变化0.687941个百分点，第一产业增加值变化0.472243个百分点，第二产业增加值变化0.547333个百分点，第三产业增加值变化1.013007个百分点。根据这一弹性关系，我们利用各年社会商品零售总额的数据估计GDP及各产业增加值的增长率。由于本模型中各变量均为对数形式，所以变化率可以按下述方式计算：

由logy1-logy2=α（logx1-logx2）可以得到，它等价于：(www.xing528.com)

，由此可得到，即增长率。具体计算过程如下：

（1）计算社会商品零售总额对数的变化，即用本年的社会商品零售总额对数减去上年的社会商品零售总额对数。

（2）将这一差额乘上各模型中揭示的GDP对数及各产业增加值对数与社会商品零售总额对数之间的系数，即弹性系数，上述4个模型中的弹性系数分别为0.687941、0.472243、0.547333和1.013007。

（3）将上述计算结果取指数并减1，便得到GDP及各产业增加值的增长率。

具体计算结果如表6-3所示。

二、GDP及各产业增加值估计增长率的相对性特征

与GDP及各产业增加值统计增长率比较，估计的增长率具有如下特征：估计的GDP增长率系统地小于统计增长率，但各个产业增加值的估计增长率却显现出不同的样式。

表6-3　典型省GDP及各产业增加值增长率估计结果

GDP估计增长率在估计的1979～2004年期间平均为7.94，而统计增长率的平均值为11.92，因此估计增长率系统地低于统计增长率，GDP估计增长率具有更为自然的波动样式。例如，1998～2001年，统计增长率每年都在10.09与10.79之间波动，而估计的增长率则在7.67与9.73之间波动；GDP估计增长率在1987年、1989年和1990年都比较低，这与中国经济当时的整体形势是吻合的；1996～2001年GDP估计增长率也基本在平均水平上下波动，这反映了东南亚金融危机对典型省经济的影响。

第一产业增加值增长率从1985～1990年相对较低，然而基本在5%上下波动，这基本符合中国第一产业的发展轨迹；1997年之后估计的增长率均高于统计增长率，而且除2004年外，基本上在5%或6%上下波动，反映出第一产业发展在这一期间相对较为平稳。

第二产业增加值估计增长率与统计增长率存在较大的差异，不仅系统地低于统计增长率，而且在众多年份低出很多。例如1992年和1993年第二产业增加值统计增长率分别为28.6%和30.6%，而估计的增长率却只有7.99%和8.70%，相差20多个百分点。不过，如果联系前面关于典型省GDP统计数据中存在的各种矛盾，似乎能够理解其中的问题。事实上，GDP统计数据中之所以会出现第二产业增加值大于GDP的问题，可能就是源于GDP统计数据中第二产业增加值增长速度过快造成的。从波动样式上来看，第二产业增加值估计增长率分别在1989年、1990年和1995年以及1996年相对较低，其他年份相对平稳，直到2003年和2004年增长率分别达到8%和9.9%，但与这两年统计增长率的17.0%和19.2%相差甚大。

第三产业增加值估计增长率与统计增长率之间的关系与前两次产业的截然不同，第三产业增加值估计增长率1998年以后基本上系统地高于统计增长率，但从1979～2004年这一期间来看，差别是很小的，或者说基本相同，估计的增长率年平均11.5%，统计的增长率年平均为11.4%；1991年以来，估计增长率与统计增长率最大绝对差发生在1994年和2004年相差近8个百分点，其余年份的绝对差基本上在可接受的范围内。

三、GDP及各产业增加值估计增长率的结构性特征

我们重新估计GDP及产业增加值增长率的动机，是要克服前面提到的因典型省GDP统计数据存在各种矛盾而无法正确评价和估计典型省经济的总量水平、发展速度和发展绩效。分析本书估计的各种增长率的结构性特征，是评价估计的增长率是否有效的一个重要标志。

1.依据估计增长率推算的增加值总量特征

如前面所指出的，典型省GDP统计数据的矛盾之一是按GDP增长率计算的GDP总量远远小于按三次产业增加值之和计算的GDP总量。为了进行比较，我们分别计算按GDP估计增长率与各产业增加值估计增长率计算的两种增加值总量。计算方法和过程如下：

（1）计算以1952年为100的各年GDP及各产业增加值指数。计算方法为：t年的GDP或增加值指数=（1+t年的GDP或增加值增长率）×（t-1）年以1952年为100的GDP或增加值指数。

（2）计算以1952年为基数的GDP或增加值总量。计算方法为：t年的GDP或增加值总量=t年的GDP或增加值指数×1952年的绝对数。

（3）将步骤（2）中计算出的三次产业增加值相加得到t年增加值总数，并与步骤（2）中计算的GDP进行比较。

（4）计算两种总增加值的绝对误差与相对误差，即（GDP总量-三次产业增值之和）与（GDP总量-三次产业增值之和）/ GDP总量。

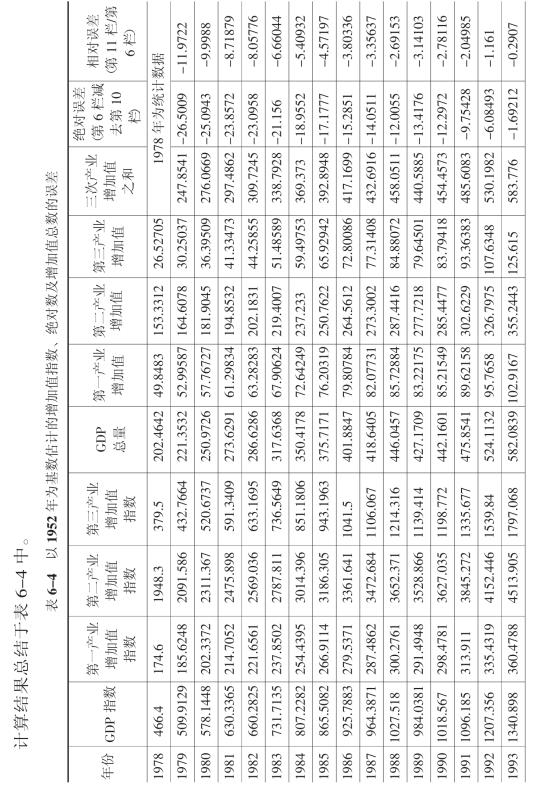
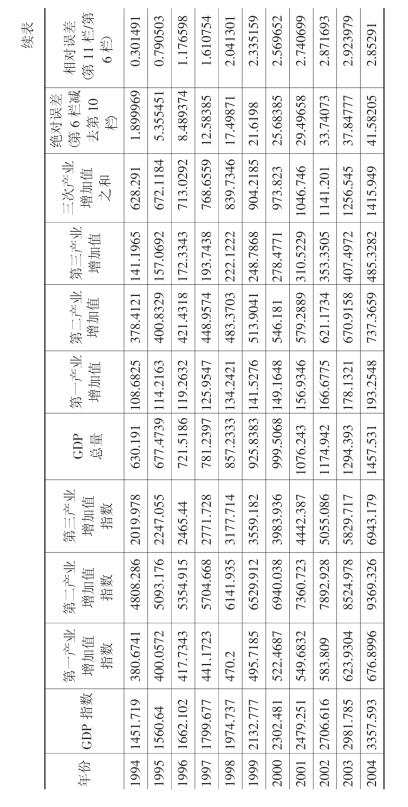
表6-4与表6-1在项目上基本相同，不同的是，表6-4是本书估计数，而表6-1是没有任何改动的统计数。表6-4中数据表明，按估计的GDP增长率计算的以1952年为基数的GDP总量，与以估计的各产业增加值增长率计算的三次产业增加值之和，虽然并不完全相等，但误差相对稳定，可视为核算的正常误差。与表6-1进行比较可知，表6-1中三次产业增加值之和不仅远远大于GDP，而且误差越来越大，而从理论上说，这两者是应该相等的。仅从这一点来看，即从数据的内在结构上看，本书估计的数据更具有合理性。然而，对比表6-1可以清楚地看出，依本书估计的增长率计算的典型省GDP总量，与统计量相差甚远。如果估计的增长率是可信的，那么，典型省的经济总量水平将从目前的3720.628亿元退回到1996年1540.925亿元的水平上去（按1952年价格水平计）。这的确是令人不愉快和不愿意承认的事。

2.依据估计增长率推算的产业结构特征

依据表6-4计算的GDP总量与各产业增加值，我们可以计算出各产业增加值占GDP或总增加值的比重，进而可能了解三次产业结构的比例关系。典型省GDP统计数据表明（见表6-1），第二产增加值已经超来了GDP，因此，无法了解其三次产业之间真正的比例关系。由于GDP与三次产业增加值之和不相等，所以我们分别以这两个数为基础计算典型省三次产业之间的比例关系。计算结果见表6-5。

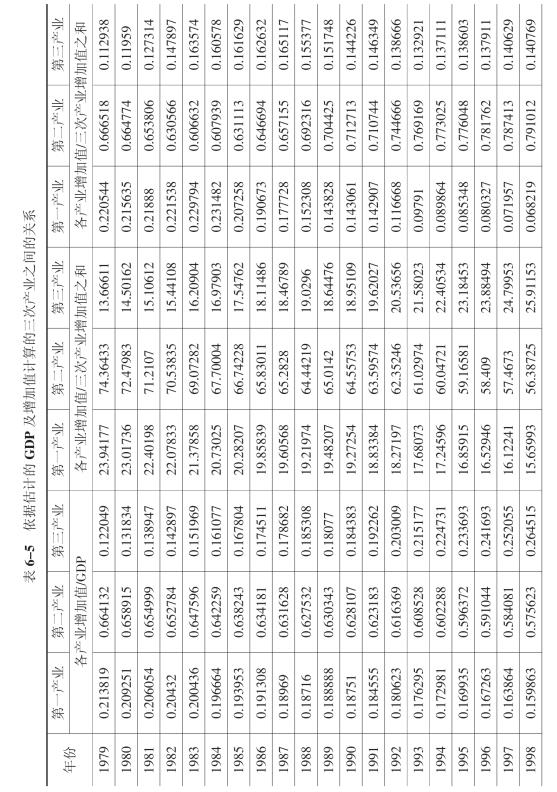
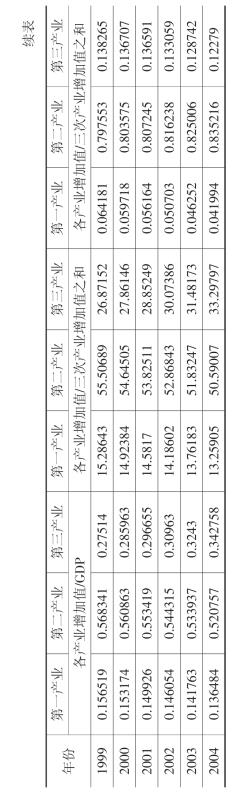
表6-6　典型省三次产业结构

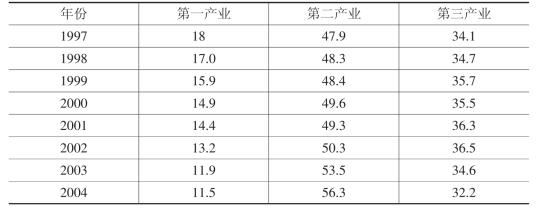
表6-5表明，无论是以估计的GDP 还是以估计的三次产业增加值之和为基础，计算出来的三次产业结构与历年典型省公布的结构基本是符合的，也与按照当年价格计算的三次产业结构相符合（见表6-6）。因此，仅从三次产业之间的比例关系来看，本书估计的GDP 增长率与三次产业增加值增长率，是符合典型省产业结构状况的。表6-5 最后三栏是按照统计增长率以三次产业增加值之和为基础（由于第二产业增加值超过了GDP，因此不可能以GDP为基础）计算出的典型省三次产业结构之间的比例关系。不难看出，表6-5中最后三栏所显示的结构关系，无论如何是存在问题的。因为它表明，自2000年起，第二产业增加值已经占到总增加值的80%以上，三次产业结构的比例关系也稳定在4% 或5%∶82%∶12%或13%这样的结构中。事实上，无论典型省经济如何发达，产业结构也没有达到这一水平。产业结构上的这一矛盾，自然来自典型省各产业增加值的统计增长率。

3.依据估计增长率推算的经济增长速度特征

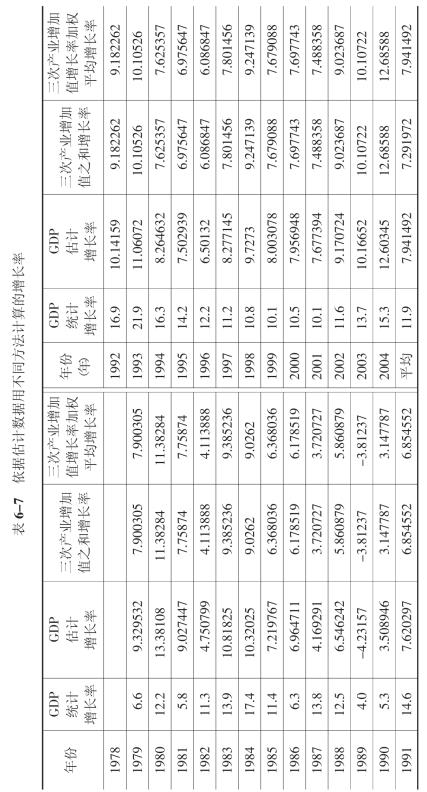
为了进一步核实本书估计的GDP增长率与各产业增加值增长率是否存在数据内部结构问题，我们计算了按三次产业增加值之和计算的增加值增长率和按三次产业增加值增长率的加权平均计算的增加值增长率。结果表明，估计的GDP增长率、按三次产业增加值之和计算的增长率以及按三次产业增加值增长率加权平均计算的增长率，基本一致（见表6-7）。这与依统计数据所做的同样计算的结果完全不同。这表明，本书估计的GDP增长率与各产业增加值增长率，从数据的内在结构上说是一致的，具有数据结构上的内在合理性。

第四节　结论与问题

本书通过分析典型省GDP统计数据的内部结构，发现了如下几个问题：

（1）典型省GDP总量上存在不一致的问题，即按GDP增长率计算的GDP总量与按各产业增加值之和计算的增加值总量存在较大的差异，而且差异越来越大。

（2）GDP结构上存在问题，即典型省第二产业增加值自1993年起超过了典型省GDP，而且即使以三次产业增加值之和为基础计算三次产业间的比例关系，结果与典型省产业结构的实际状况也是相矛盾的。

（3）经济增长速度存在问题。典型省GDP增长率与按三次产业增加值之和计算的增加值增长率、按三次产业增加值增长率的加权平均计算的总增加值增长率之间，存在较大的差别。

本书利用GDP及各产业增加值模拟模型，依据变量间协整关系，重新估计了典型省GDP及各产业增加值的增长率，估计出的数据不仅不存在上述各种矛盾，而且从产业结构上看，更符合典型省经济的实际状况。

然而，本书的模拟模型是建立在约束回归下的模型，存在低估各种增长率的可能性，但究竟会低估到什么程度，现在还没有证据加以说明。不过，本书估计的典型省经济增长率，与其他学者利用标准的GDP核算方法估计的中国经济增长率相比，均要略高一些，特别是高于麦迪森（Maddison，1998，Table C-5）、任若恩（Ren，1997，Table 5.3）、亚当斯—陈（Adams和Chen，1996，Table 4）、伍晓鹰（2000）和阿尔温·扬（Young，2000）等人对中国经济增长率的估计。如果说，典型省的经济增长率高于中国各地的平均水平是客观事实的话，那么，本书估计的可信性，可从这一对比中得到一些认证。同时，如果认为本书的确系统地低估了典型省的经济增长率，那么，可对估计增长率做等比例的上调，这样既可以保持数据间的一致性以及产业结构间的一致性，又能够准确地估算典型省的经济总量水平和发展速度。

无论如何，在没有获得进一步的证据之前，我们无法给出本书的估计是正确的这一结论。我们更愿意将本书的估计作为进一步研究典型省经济增长数据乃至其他省经济增长数据的一个开端，因为典型省GDP统计数据中存在的各种问题，恐怕在其他地方也同样存在。

参考文献

1. Adams，F. Gerard and Yimin Chen，“Skepticism about Chinese GDP growth -the Chinese GDP elasticity of energy consumption”，Journal of Economic and Social Measurement，22，231-240，1996.

2. Maddison，Angus，Chinese Economic Performance in the Long Run，OECD Development Centre，Paris，1998.

3. Ren，Ruoen，China - Economic Performance in An International Perspective，OECD Development Centre，Paris，1997.

4. Ren，Ruoen and Chen，Kai，“An expenditure - based bilateral comparison of gross domestic product between China and the United States”，Review of Income and Wealth，Series 40，1，377-94，1994.

5. Woo，Wing Thye，Chinese Economic Growth: Sources and Prospects，paper presented at Economics Discipline Seminar，RSPAS，Australian National University，1996.

6. Wu，Harry X.，“The long -mn comparative labour productivity in Chinese and US manufacturing，1952 -97”，in Peter Lloyd and Xiaoguang Zhang（eds.），China in the Global Economy，Edward Elgar Publishing Ltd.，London，2000.

7. Young，Alwyn，2000. Gold into base metals：productivity growth in the people’s republic of China during the reform period.