中国经济增长与能源消费：协整与误差修正模型实证

第三章　经济增长与能源消费：基于协整与误差修正模型的研究

第一节　引　言

经济增长与能源消费之间的联系，一直是学术界和政府研究部门关注的热点，这是因为经济增长与能源消费之间的因果方向具有重大的政策含义。如果存在从经济增长到能源消费的单向因果关系，那么，这一经济是非能源依赖型经济，因而节能政策的实施对经济增长的负面影响可能就非常小，甚至不存在负面影响（Jumbe，2004）；如果存在从能源消费到经济增长的单向因果关系，那么，这一经济就是能源依赖型经济，能源消费的降低可能会影响经济增长（Masih和Masih，1998）；如果经济增长与能源消费之间不存在因果关系，即所谓满足“中性假说”（neutrality hypothesis）（Yu和Choi，1985），那么，经济增长与能源政策并没有什么必然的联系；如果经济增长与能源消费之间存在双向因果关系，那么，这表明该经济体是经济增长与能源消费相互依赖型的。为了保持经济增长与能源消费相互适应，必须综合运用各种政策，通过政策的最佳组合实现经济增长与能源消费的协调发展。

为了理解和发现能源消费与经济增长之间的内在联系与证据，学者们对经济增长与能源消费之间的关系做了大量实证性研究工作。但直到今天，人们也没有发现经济增长与能源消费之间普遍存在的长期或短期关系的确凿证据。

Kraft和Kraft（1978）是学术界公认的从实证角度研究经济增长与能源消费之间关系的学者。他们利用美国1947～1974年的数据，发现经济增长与能源之间存在从经济增长到能源消费之间因果关系的证据。Akarca和Long（1979）运用美国月度数据的研究，支持了这一结论。后来的研究，由于运用不同的时间段，产生了不同的证据，或者支持Kraft和Kraft的结论，或者与其相反（Abosedra和Baghestani，1989；Yu和Choi，1985；Cheng，1995；Hwang和Gum，1991；Erol和Yu，1987）。由于研究结果具有时空依赖性，因此，学者们几乎对世界大部分国家都进行了实证研究。Masih和Masih（1996）、Glasure和Lee（1997）以及Asafu-Adjaye（2000），对截止到2000年的文献进行了较为全面的综述和总结。Chien-Chiang Lee将直到2005年对发展中国家实证研究的文献进行了总结，在此基础上，本书总结了不同学者对不同国家实证研究的结果（见表3-1）。

通观有关经济增长与能源消费的研究文献，我们可以得到如下几个结论：

（1）经济增长与能源消费之间存在四种类型的关系：经济增长到能源消费的因果关系；能源消费到经济增长的因果关系；经济增长与能源消费之间存在双向因果关系；经济增长与能源消费之间不存在因果关系。

（2）不同国家存在不同的经济增长与能源消费之间的因果关系；同一个国家在不同时期存在不同的经济增长与能源消费之间的关系（见表3-1）。

表3-1　发展中国家（地区）经济增长与能源消费因果关系检验结果比较

（3）因果关系的检验方法不同，会得到不同的因果关系：首先，许多早期的研究运用OLS方法估计线性模型，根本不考虑所研究的时间序列的性质。现代计量经济学表明，经济领域中许多时间序列都是非平稳的（Granger和Newbold，1974）。不考虑时间序列的平稳性而直接进行回归估计，很可能得出变量之间错误关系的结论，即所谓的“伪回归”。其次，在过去的大约10年中，人们遵循基于Granger（1969）和Sims（1972）提出的检验方法，对经济增长与能源消费进行了双变量因果关系检验，并得出了各自的结论。然而，正如J. Asafu-Adjaye（2000）所指出的，标准的或传统的Granger-Sims检验，由于不能探索其他的因果方向，因而可能得出错误的或相互矛盾的因果关系。例如，Glasure 和Lee（1997）分别利用标准的Granger检验方法和协整与误差修正模型，对韩国与新加坡的经济增长与能源消费进行了检验，结果发现，利用协整和误差修正模型时，两国的经济增长与能源消费均存在双向因果关系；而运用标准的Granger方法进行检验时，韩国的数据不存在因果关系，而新加坡则存在从能源到经济增长的因果关系。

最近几年，有关中国经济增长与能源消费关系的研究开始大量出现（林伯强，2001，2003；马超群等人，2004）。这除了从上述意义上探索经济增长与能源消费关系外，还有更深一层的原因，即从能源消费与经济增长之间的关系探究中国经济增长速度可信性问题。

中国经济的发展速度，在世界经济萧条的大环境下，持续地处在较高水平上。这一现象，在令人们称奇的同时，也引起人们对中国经济增长速度的怀疑，与此同时，中国国家统计局核算的中国GDP增长速度，与各省数字的加权平均数据之间的差距也在不断扩大（李德水，2004）；有关基层政府在GDP统计上存在弄虚作假的报道，以及统计执法检查中发现的一系列统计违法问题（赵宝珍，1997；刁恒昌等，1996；统计数字质量研究课题组，1995；王金海，1998；于洪彦、许松山，1990；赵鹏，1998），都成了部分学者对中国GDP增长速度质疑的直接理由。

为了从经验证据上系统地检验中国GDP增长速度是否被人为地高估了的假设，人们从不同方面进行了检验（蔡、王美艳，2002；周建，2002）。由于经济增长与能源消费之间的紧密关系，人们自然而然地会从能源消费与经济增长之间关系的角度加以试探性研究，进而引发了关于中国GDP增长速度与能源消费之间关系的讨论。

对中国GDP增长速度提出质疑的西方学者之中，素有“国际经济乌鸦”之称的克鲁格曼（Krugman）教授和匹茨堡大学的罗斯基（Thomas G. Rawski）教授，表现得最为激进。克鲁格曼毫无根据地声称，看中国经济增长数据，就像看一部科幻小说，中国的经济数据是一堆不可置信的符号体系。罗斯基连撰数文，根据中国GDP与能源消费、就业等相关数据间的不协调性，认为中国的GDP数据不可信（Rawski，1993；2001a，2001b）。罗斯基的充满争议的文章，引发了中外学者对中国经济增长与能源消费之间关系研究的一个新浪潮。

利用省级数据探索能源消费与经济增长的关系以及GDP统计数据的可信性，更具有根本性，更具有重要意义。因为全国数据是依据省级数据调整而成的，如果省级数据是准确的，那么中国经济实际增长态势将较全国数据显示得更为可观，理解中国经济增长与能源消费关系就更具有微观基础。

本书选择的典型省是中国经济和人口大省之一，自2002年以来，典型省GDP在全国名列第三位，占全国GDP总量的1/10左右，人口居全国第二位。同时，典型省经济结构与经济发展格局与全国具有相似性。因此，研究典型省GDP增长与能源消费关系，不仅对于典型省具有现实意义，而且对于理解中国经济也具有重要意义。近年来，虽然国内外学者对中国的能源消费与经济增长之间的关系进行了大量的研究，但有关典型省能源消费与经济增长之间关系的实证研究却非常少见。本书运用目前在学术界广泛关注的计量经济方法——协整和误差修正模型，建立典型省经济增长与能源消费之间关系模型，探索和透视如下三个方面的问题：一是典型省经济增长与能源消费之间的因果关系以及方向；二是典型省经济增长可信度与可信区间；三是识别典型省经济结构的转变与能源消费变动趋势之间的关系。

第二节　平稳性与协整性检验

本书运用目前在政策分析和经济领域广泛应用的协整理论模型，实现对上述三个问题的探索。研究经济变量之间关系，有两种基本的范式：一是根据理论分析演绎地提出变量间的关系；二是根据直观经验归纳地提出变量间的关系。然而，这两种方式界定的变量间关系都需要以经验检验为支撑，本书主要从经验的角度，对变量间关系进行实证性检验。

一、协整的直观描述及其严格界定

传统上，当人们实证地检验变量间关系的论断时，以反映变量间关系的系数的t统计量是否显著，以及反映自变量对因变量解释能力的R2是否足够大，作为肯定或否定变量间关系论断的判断准则。然而，人们逐渐发现，当变量存在趋势或变量为非平稳时间序列时，依据t统计量和R2准则，判断变量间存在某种关系时，却具有潜在的“虚假性”，即可能出现所谓的伪回归（spurious regressions）（Granger和Newbold，1974）。事实上，Granger和Newbold发现，在回归方程中，如果变量是存在确定趋势的时间序列，且DW统计量较小而判决系数较大，即R2> DW，则这一回归一般都是伪回归。

由于经济学家（Nelson和Plosser，1982）发现，经济领域中的大多数时间序列都是非平稳的（non-stationary），因此，出现伪回归的情形非常普遍。通常，为了避免因时间序列的非平稳性而引发的这一问题，人们利用变量的一阶差分（first differences）进行回归。然而，利用差分形式变量的回归，表明的是变量间的短期关系或非均衡关系；只有利用水平变量的回归，表明的才是大多数经济理论所指称的变量间的长期或均衡关系。

为了建立变量间的长期关系方程，必须识别出具有长期关系的时间序列的特征。事实上，如果所研究的具有趋势的时间变量具有相同的趋势，或者说具有相同的“波长”，那么，这类时间序列间的回归关系，就有可能不是伪关系，因而通常的t统计量和F统计量就有可能是有效的。这种非平稳时间序列间的“同时性”（synchrony），正是“协整”概念的来源（Gujarati，1995）。因此，为了研究变量间的长期关系，必须研究变量间是否具有这种协整的性质。

协整分析被认为可能是20世纪80年代以来计量经济学中最具革命性意义的发展。简单地说，协整就是具有向上或向下趋势的非平稳时间序列随着时间的流逝而共同“漂移”（drift together），犹如人与其影子共同移动一样。不同变量的这一共同漂移使得变量间可能存在长期线性关系，因而可以预期经济变量之间存在均衡关系。但是，如果变量间不存在这种长期关系，则这些变量之间就是“非协整”（not cointegrated）的。

一般而言，协整分析是估计非平稳时间序列间长期或均衡关系的一种方法，也是设定、估计和检验动态模型的一种新技术，因而可用以检验经济理论或经验命题的有效性。此外，协整分析还可用于研究变量间短期或非均衡关系，因为可以利用协整方法所获得的长期参数来探索短期或非均衡关系，即所谓的“误差修正模型”。

用严格的语言来表述，协整的概念可以界定如下：两个时间序列Yt和Xt是（d，b）（d≥b≥0）阶协整的，如果两个序列都是d阶单整的，并且存在两个序列的一个线性组合（a1Yt+a2Xt），其为（d - b）阶单整的。即如果Yt～I（d），Xt～I（d），且a1Yt + a2Xt～I（d - b），那么，Yt，Xt～CI（d，b）。

上述协整概念表明，如果Yt～I（1），Xt～I（1），且Yt =β0+ β1Xt，那么，当Yt-β0-β1Xt=0时，Yt和Xt实现了长期均衡，即Yt和Xt之间的关系可表示为：

则εt～I（0），且E（εt）= 0。Stock（1987）证明，对于大样本来说，方程（3-1）的OLS估计量是“超一致的”（superconsistent），即OLS估计量是一致的而且非常有效，其回归系数迅速地收敛到总体的真值。不过，Banerjee等人（1986）证明，对于小样本来说，OLS估计量是有偏的，而且其偏度水平依赖于R2的值：R2越大，其偏度水平越低。因此，Granger（1986）认为，为了避免伪回归情形的出现，在进行回归分析之前，应该检验所涉及的变量间是否是协整的。

二、平稳性检验

由于在协整检验中，必须先对变量进行平稳性检验。因此，先说明一下本书使用的平稳性检验的方法。目前，计量经济学已经发展出了各种各样的平稳性检验方法，但由于拓展的Dickey-Fuller（Augmented Dickey-Fuller, ADF）检验方法更为普遍一些，因此，本书使用ADF检验方法。

假设时间序列Xt由下列过程生成：

那么，其差分形式可表示为：

其中δ=φ1+φ2+…+φq-1，其他δj是φj的一般函数。ΔXt可以分为三种情况，即对应于如下三种检验模型：

上述三种模型对应于ΔXt的三种不同的数据生成方式。当事先不知道ΔXt是由哪一种方式生成的时候，人们对检验顺序提出了不同的建议。Holden与Perman（1994）以及Enders（1995）对这些建议进行了总结，并提出了一种被人们广泛接受的检验顺序。这一检验顺序可归结为如下要点：

（1）坚持“自上而下”的原则，即从数据生成的最一般的形式开始，逐渐过渡到特殊的情形。

（2）如果知道时间序列含有漂移项或时间趋势，则运用标准正态分布检验存在单位根的零假设。

（3）由于单位根检验具有较低的拒绝存在单位根的零假设的能力，因此，在“自上而下”检验的任何一步中，如果零假设被拒绝，则停止检验，可以断定这一时间序列是平稳的。

三、协整的检验

两个常用的协整检验方法是Engle和Granger（1987）提出的两步法或拓展的Engle -Grangers（Augmented Engle -Granger, AEG）检验，以及Johansen和Juselius提出的完全信息极大似然法（Johansen和Juselius，1990；Johansen，1995）。

Engle-Granger的两步法适应于一元变量的情形，而Johansen 和Juselius的完全信息极大似然法适应于多元变量的协整问题。这一方法不仅提供了一个估计方法，而且还提出了检验协整向量个数及经济理论所设条件的显示方式。运用这一方法估计协整系统的相应参数，一方面可避免因施加特定的约束条件而导致模型的错误设定；另一方面可更一般地检验存在多个协整关系的零假设。由于本书未涉及多变量间协整关系，因此运用Engle-Granger的两步法对数据进行检验。

Engle-Granger的两步检验方法遵循如下步骤：

（1）利用单位根检验方法确定变量的单整阶数。这一过程可分为三种情况：①如果两个变量的单整阶数相同，那么需要研究其协整性，进入下一步；②如果两个变量的单整阶数不同，那么基本可以得出两个变量不是协整的结论；③如果两个变量是0阶单整的，即是平稳的，那么整个检验过程停止，可利用标准回归技术进行分析。

（2）如果两个变量具有相同的单整阶数，如均为I（1），则利用OLS估计长期均衡方程Yt=β0+β1Xt+εt，并保存残差序列et。

（3）两个变量协整的必要条件是其均衡误差必须是平稳序列。为检验残差序列是否为平稳的，则运用前面介绍的ADF方法检验如下方程：

（4）根据下列假设判断et是否为平稳序列：

H0：δ= 0，如果tδ>τ，则序列et是非平稳的，两个变量不是协整的；

Ha：δ< 0，如果tδ<τ，则序列et是平稳的，两个变量是协整的。

第三节　变量界定与实证性检验结果

为了探索典型省经济增长与能源消费之间的关系，本书选用的代表产出性的变量有典型省GDP、第一产业、第二产业与第三产业以及工业增加值，代表能源消费的变量有能源总量，不含电力的能源消费量以及电力，并对每一种产出与每一种能源消费量之间的关系进行了详细的考察。

各种产出数据都以不变价格表示，因而具有可比性。各能源消费量均用万吨标准煤测量。本书中所有产出数据和能源消费数据均源自于典型省各年的统计年鉴。为了消除异方差性以及使模型更具有实际意义，本书中所有产出数据与能源消费数据均进行了对数变换，因而系数均表示产出与能源消费之间的弹性关系。本书中变量定义如下：lrgdp，实际GDP的对数；lragri，第一产业实际增加值的对数；lrsec，第二产业实际增加值的对数；lrtert，第三产业实际增加值的对数；lindust，工业实际增加值的对数；lele，电力消费的对数；lenergy，不包含电力的能源消费的对数；lene，能源消费总量的对数。

一、数据的平稳性或单位根检验

本书运用前面介绍的ADF（Augmented Dickey-Fuller）单位根法，检验了序列的平稳性。本质上，对任意变量Zt，检验零假设Zt～I（1）相当于检验ΔZt是平稳的，即不存在单位根。本书ADF单位根检验过程基于如下两个一般形式的OLS回归方程：

其中T表示线性趋势，k为被选做使εt成为白噪声残差的滞后阶数。ADF检验遵循前面提出的顺序。如果α1显著小于零，则可拒绝存在一个单位根的零假设，得出Zt～I（0）的结论；检验Zt中存在一个单位根（Zt～I（1））的零假设相当于检验公式（3-9）中α1= 0。如果α1= 0并且γ1显著小于零，则可得出Zt～I（1）的结论。如果γ1= 0，则ΔZt中存在单位根，因此其可能是Zt～I（2）序列。

在利用AIC与SC准则确定变量的滞后阶数的基础上，对所有产出数据和能源消费数据进行了检验。检验结果表明，水平数据都不能拒绝存在单位根的原假设，而所有数据的一阶差分，都分别在1%和5%的显著性水平上拒绝了存在单位根的原假设。这表明，本书中所有变量均为一阶单整。为了节省篇幅，表3-2只报告了一阶差分后序列的单位根检验结果。

表3-2　变量的单位根的检验

注：*（**，***）indicates a significance level of 10%（5%，1%）。本书所有计算都运用Eviews 3.1完成。

二、变量间的协整关系检验

表3-3　变量的协整检验

本书运用前面介绍的EG两步法对每一对变量进行了协整检验。检验结果表明（见表3-3），能源消费总量与典型省GDP、农业增加值、第三产业增加值、工业增加值是协整的，与第二产业增加值不是协整的；不包含电力的能源消费总量与GDP、农业增加值、第二产业和第三产业增加值以及工业增加值是协整的，即与所有的产出变量是协整的；电力与所有产出变量都不是协整的。这说明，不包含电力的能源消费与各产出变量之间有一种共同的长期趋势，而电力消费与各产出变量之间不存在共同的长期趋势。这可能是由于电力一直不是典型省生产用重要能源之一的原因。自1995年以后，电力占典型省一次能源消费总量的0.01%左右，占终端能源消费量的14%～22%，而原煤、原油则占典型省能源消费总量的80%以上。

三、变量间的因果关系检验

各种能源消费与产出水平存在的协整关系，只是说明这些变量具有共同的变动趋势。为了理解典型省的经济类型（能源约束型、增长诱致的能源需求型），以及能源消费与经济增长之间的相互关系，有必要了解这两者之间的因果方向。在回归方程中，一个解释变量Xt影响因变量Yt，意味着解释变量Xt的变化引起因变量Yt的变化。这就是所谓的变量间因果关系。

根据变量间引致变化的方向不同，可分为两种情况：单向因果关系，即变量Xt的变化引致变量Yt的变化，但变量Yt的变化并不引致变量Xt的变化；双向因果关系，即变量Xt和变量Yt相互引致对方的变化。由于在大多数情况下，人们并不知道变量间的因果方向，因此，人们设计了各种各样的检验方法来识别变量间的因果方向（Sims，1972；Geweke等人，1983；Granger，1969，1988）。其中最为著名的也是目前应用最为广泛的检验方法是Granger（1969）提出的方法。Granger的因果检验基于这样的事实：将来不可能引起现在或过去发生变化。从这一基本事实出发，Granger以类比的方式提出了一种因果关系，即如果一个变量的加入提高了对另外一个变量变化的预测能力，则前者为后者的原因。这一检验方法基于对下列两个方程的检验：

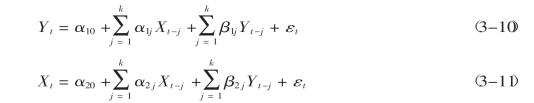
基于这两个方程，我们可区分出以下三种情况：

（1）如果｛α11，α12，…，α1k｝≠0，而且｛β21，β22，…，β2k｝= 0，那么存在由Xt到Yt的单向因果关系，表示为Xt→Yt。

（2）如果｛α11，α12，…，α1k｝＝0，而且｛β21，β22，…，β2k｝≠0，那么存在由Xt到Yt的单向因果关系，表示为Yt→Xt。

（3）如果｛α11，α12，…，α1k｝≠0，而且｛β21，β22，…，β2k｝≠0，那么存在Xt和Yt的双向因果关系，表示为Xt圳Yt。

为了检验关于方程（3-10）和方程（3-11）系数是否为显著，可以使用如下的Wald F统计量：

其中SSRu非约束回归方程的残差平方和，SSRr为约束回归方程的残差平方和。

检验假设可以叙述如下：

H0：X不是Y的Granger原因，即｛α11，α12，…，α1k｝= 0，判断准则为Fc小于F的阈值。

Ha：X是Y的Granger原因，即｛α11，α12，…，α1k｝≠0，判断准则为Fc大于F的阈值。

H0：Y不是X的Granger原因，即｛β21，β22，…，β2k｝= 0，判断准则为Fc小于F的阈值。

Ha：Y是X的Granger原因，即｛β21，β22，…，β2k｝≠0，判断准则为Fc大于F的阈值。

本书运用上述方法对典型省经济产出数据与能源消费数据进行因果关系检验，结果如表3-4所示。表3-4表明，典型省大部分产出变量与大部分能源消费变量之间存在单向的因果关系，即经济增长为能源消费的Granger原因。

表3-4　变量间Granger因果关系检验

具体地说，典型省GDP是总能源（lene）、不包含电力的能源（lenergy）消费的Granger原因，即经济增长导致能源需求的增加，但GDP与电力消费（lele）之间不存在因果关系。这其中的原因虽然还不太清楚，但可能与典型省的经济结构有关。工业增加值是总能源、不包含电力的能源以及电力消费的Granger原因，这说明，工业经济的增长导致各种能源需求的增加。这一结论与典型省能源消费与工业经济增长之间的关系非常吻合。第一产业增加值是不包含电力的能源消费的Granger原因，而与总能源、电力消费之间不存在Granger因果关系。由于第一产业能源消费主要由煤炭与电力构成，同时又与电力之间不存在Granger因果关系，这说明第一产业增加值是煤炭消费的Granger原因。第二产业增加值是总能源与不包含电力的能源消费的Granger原因，同时电力消费是第二产业增加值的Granger原因。因此，电力消费的变动应该能够反映第二产业增加值的变动情况。第三产业增加值是总能源与不包含电力的能源消费的Granger原因，而与电力消费不存在Granger因果关系，这说明第三产业的发展导致总能源和不包含电力的能源需求的增加。由于典型省第三产业消费的能源主要是原煤、原油及其制品、电力与热力，因此，从这一结构上来看，第三产业的发展主要导致对原煤、原油及其制品、电力与热力需求的增加。

四、协整与误差修正方程

根据协整理论，若变量间存在协整关系，则可以用误差修正模型描述变量间的长期均衡与短期波动关系。根据前面的协整检验，可以得到如表3-5所示的协整方程，据此可以建立误差修正方程。

运用Hendry的从一般到特殊的建模技术，并依次剔除各变量的不显著滞后期，可以得到较为简明的如下几个误差修正模型：

表3-5　协整方程（根据因果方向）

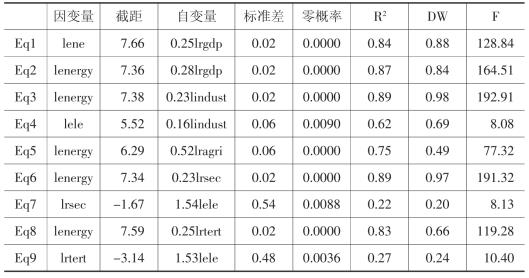
其中，每项下面括号中的数字为t统计量，各式中右边第二项系数表明两个变量间的短期关系，右边第三项（ECMi）系数表明对偏离长期均衡关系的调整。

由于表明短期关系的系数均为负数，说明在短期内，能源消费与GDP及各产业GDP均呈现出负相关关系，即经济增长的能源消费弹性是下降的。这与能源消费与经济增长的长期正相关关系形成鲜明的对照。在短期内，GDP增加1个百分点，将导致能源消费需求下降0.88个百分点，将导致不含电力的能源消费需求下降0.69个百分点，工业增加值增加1个百分点，将导致能源消费下降0.49个百分点，将导致不含电力的能源消费需求下降0.363个百分点。而在长期，GDP增加1个百分点，将导致能源消费需求增加0.25个百分点，工业增加值增加1个百分点，将导致能源消费增加0.23个百分点。

上述各方程表明，误差修正项（ECMi）的系数均为负，说明误差修正项（ECMi）的校正机制是，当ECMi为正时，ECMi对能源消费的差分有减少的作用；相反，当ECMi为负时，ECMi对能源消费的差分有增加的作用。ECMi系数的大小表明调整均衡偏差的幅度，该系数越大，说明当能源消费与GDP出现长期偏离均衡时，变量回归到均衡状态时调整的速度越快。例如，ECM1（-1）的系数为-0.60，说明短期内对能源消费与经济增长长期均衡关系调整幅度为每年60%，即长期稳定关系的失衡，对短期能源消费波动的影响很大。在公式（3-14）、公式（3-15）和公式（3-16）中，ECM10（-1）、ECM3（-1）和ECM6（-1）的系数都很大，表明短期内对工业及第二产业产出与能源消费长期关系失衡的校正强度很大，每年都在72%以上，因此，能源消费与经济增长之间关系的短期波动主要是由于工业或第二产业产出水平与能源消费之间关系的波动引起的。

第四节　经济结构、能源消费与经济增长的可信性区间

第三节主要讨论了典型省经济增长与能源消费之间的协整关系、因果关系与误差修正模型。第三节的讨论表明，典型省经济增长与能源消费之间存在协整关系，即存在长期稳定关系，GDP每上升1个百分点，将导致能源消费增加0.25个百分点。但短期内经济增长与能源消费之间的关系相反，且波动较大，短期内滞后一期的GDP增长1个百分点，将导致能源消费下降0.88个百分点。典型省存在经济增长到能源消费的单向Granger因果关系，即经济增长引致能源消费的增加。但各能源构成（不含电力的能源与电力）与GDP构成（第一、第二和第三产业产出）之间的关系，特别是电力消费与第三产业之间的关系比较复杂，同时如何估计GDP增长的可信区间，也没有论及。因此，本节主要讨论经济结构与能源消费之间的关系以及经济增长的可信性区间问题。

一、经济结构与能源消费

表3-5中所列协整方程表明，经济的不同结构对能源（结构）需求的影响强度存在很大差别。第一产业增加值每提高1个百分点，将导致能源消费增加0.47个百分点，导致不含电力的能源消费增加0.52个百分点；工业增长值每提高1个百分点，将导致不含电力的能源消费增加0.23个百分点（与第二产业的情形一致），只引致能源消费增加0.20个百分点，但只引致电力消费增加0.16个百分点；第三产业增加值每提高1个百分点，将导致能源消费增加0.22个百分点，导致不含电力的能源消费增加0.25个百分点。这一现象有些令人不解，因为第一产业的能源消费弹性最高，第三产业次之，第二产业最低，与各产业能源消费的实际情况相矛盾。

出现上述问题的原因，可能与单独考虑各不同经济结构与能源消费之间关系引致的。为了消除上述出现的不同经济结构能源消费弹性的有偏情况，我们对能源消费的对数作各产业增加值占GDP比例的对数的同时回归，结果如下：

公式（3-19）中，lene代表能源消费的对数，sec代表第二产业产出水平占GDP比例的对数，即log（第二产业增加值的实际值/实际GDP），tert为log（第三产业增加值的实际值/实际GDP），agri为log（第一产业增加值的实际值/实际GDP）。

公式（3-19）比较准确地反映了经济结构变化与能源消费之间的关系：首先，GDP构成的各产业对能源消费的影响方向，合乎经验关系，第一产业、第三产业产出水平在GDP构成中比例的提高将导致能源消费降低，第二产业产出水平在GDP构成中比例的提高在一定范围内将提高能源消费；其次，产业结构比较好地解释了能源消费的变化，产业结构变化解释了能源消费变差的87.3%；最后，各产业产出水平在GDP中的比例对能源消费的影响在统计上和经验上都非常显著。

公式（3-19）表明，在经济结构不变的情况下，第一产业产出占GDP的比例每提高1个百分点，将导致能源消费下降2.326个百分点，第三产业产出占GDP的比例每提高1个百分点，将导致能源消费下降1.072个百分点。由此可以看出，第一产业产出水平的提高，对能源消费降低的影响比第三产业的大得多。但如果经济结构发生变化，则上述各关系均要发生变化。公式（3-19）中的最后一项，即第二产业产出水平占GDP的比例的平方项，统计上非常显著，说明第二产业产出水平对能源消费的影响随着产出水平的提高而增加，但这种增加是规模递减性的。这说明第二产业产出水平的能源消费弹性具有先上升后下降的趋势，因而能源消费与第二产业产出水平的关系是一个非线性关系，进而说明能源消费与GDP的关系也是一个非线性关系。因此，从能源消费的线性变化中不能推出GDP的确切变化，因为能源消费不仅与GDP总量相关，而且与GDP的结构，即经济结构相关。

公式（3-19）中反映出的各产业对能源需求的影响与表3-4中反映出的影响形成鲜明对照，这种差异同样源于经济结构的影响。表3-4中的关系只考虑了各个产业与能源消费的关系，没有考虑到经济结构问题，而公式（3-19）中将经济结构作为控制变量，因此，更为准确地反映了能源消费与经济结构及经济增长之间的关系。

二、基于能源消费与结构变量估计的GDP增长的可信性区间

既然典型省GDP增长与能源消费之间，以及能源消费与经济结构之间，都呈现出非线性关系，那么，从能源消费与经济结构来探索GDP增长的可信性区间，也应该反映出这种非线性关系。下面的回归方程说明了这一点。

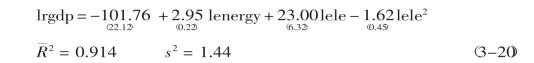
其中括号内数字为标准误差，所有变量的p值小于0.0016，其他各变量定义与前面相同。公式（3-20）表明，各个变量在0.2%的显著性水平上均为统计上显著，而且能源对数的变动解释了典型省GDP对数变差的91.4%。电力消费的平方项lele2在0.2%的显著性水平上显著，表明经济增长与能源消费显现出非线性关系，且经济增长的电力消费弹性具有规模递减效应。

同时，从经济生产过程上来说，GDP的产生由两部分构成：一部分需要消费能源；另一部分不需要消费能源。从前面关于各产业增加值与能源消费的协整关系和因果关系来看，与电力既无协整关系也无因果关系的是第三产业增加值，因此，在利用能源解释GDP增长时，未能被解释变量解释的那部分肯定与能源消费关系最弱的那部分增加值有关。

据此，根据能源消费与GDP增长各自的数据结构，我们遵循亨德瑞（Hendry）提出的从一般到特殊的建模理念，经过模型筛选和剔除统计上不显著的变量，得到了从能源消费和经济结构到经济增长的如下预测模型：

其中括号内数字为标准误差，其他各变量定义与前面相同。公式（3-21）表明，所有变量均在0.5%（即所有变量的p值都小于0.0055）的显著性水平上显著。该模型解释了典型省GDP变差的99.8%，同时，DW统计量为1.65，经验证，残差序列不存在序列相关。显然，公式（3-21）在解释GDP变差方面，较公式（3-20）为优。

虽然公式（3-21）表明，能源消费与第三产业产值变动能够解释GDP变差的99.8%，但由于数据的性质，我们并不能据此对公式（3-21）的模拟能力和预测能力做出优劣的判断。从理论上说，评价和显示模型模拟和预测能力的指标主要有以下几个指标：模拟误差的均方根，其定义为rms error=。rms error度量了变量的模拟值与实际值之间的距离，通过将其与变量的均值进行比较，能够显示出模拟误差的大小。另外一个能够用来评价拟合程度的统计量是模拟误差均方根比，它的定义是，它的大小反映了模型模拟数据结构的能力，从而反映了模型的预测能力。不过，模拟误差均方根比存在的一个严重问题是，它只反映了模拟优度，并没有考虑到数据转折点问题。与模拟误差均方根比有关的、能够反映数据转折点的统计量是Theil不等系数（Theil’s Inequality Coefficient），其定义如下：

其中，为Yt的模拟值，为真实值或实际值，T为模拟的时期数。U的分子是模拟误差均方根，分母的比例换算因子是使U保持在0～1之间。因此，Theil不等系数度量的是相对的模拟误差的均方根（rms error）。如果U = 0，那么意味着对所有的t都有模拟值等于实际值，即模型与数据完全拟合；如果U = 1，则意味着模型的模拟和预测能力很差。

其中，，σs和σa分别是序列和的平均值和标准差，ρ是它们的相关系数，即，因此，U可以分解为以下三个不等比率：

由于UM，US，UC分别显示了U的来源，因而按其所代表的误差来源分别被称为偏差比率、方差比率和协方差比率。

偏差比率是衡量系统误差的指标，因为它表明了模拟数列平均值偏离真实数列平均值的程度。不论不等系数U的值为多少，我们都希望偏差比率很接近0。一个较大的偏差比率（例如，超过0.1或0.2）意味着模型存在系统偏差。

方差比率表明了模型模拟被研究变量变化程度的能力。如果方差比率很大，则说明真实数列波动很大而模拟数列波动很小，或者真实数列波动很小而模拟数列波动很大。这表明模型没有很好地模拟真实数据的转折点，因而也不是一个好的预测模型。

协方差比率测量的是非系统误差，即它衡量剔除了偏离平均值以后的误差。由于在一般情况下很难做到模型具有100%的模拟能力，使模拟和预测结果与实际数据完全吻合，因此，这部分误差稍大一点并不能说明什么。事实上，对于任何的不等系数U > 0，最理想的模拟和预测模型是使UM= US= 0，UC= 1。

为了验明公式（3-21）的模拟与预测能力，我们计算了前面评价模型模拟与预测优度的几个指标：模拟误差的均方根rms error =0.033064，绝对值误差均值为0.025831，绝对值百分比误差均值为0.365172，Theil不等系数（U）为0.002194，偏差比率（UM）为0.000000，方差比率（US）为0.000372，协方差比率（UC）为0.999628。由于方差比率相对较小，协方差比率相对较大，根据最理想的模拟与预测模型的条件，可知公式（3-21）应具有较为优良的模拟与预测能力。

为了说明这一点，以及理解典型省GDP增长速度的可信度，表3-6给出了根据公式（3-21）计算的模拟值，以及模拟值与实际值的相对误差，并给出了各年GDP数据的95%置信区间。

表3-6中数据表明，公式（3-21）给出的GDP对数的模拟值与GDP对数的实际值之间的相对误差，大于1%的只有两个年份，其余均在1%以下。其中模拟值与实际值相对误差小于1%大于0.5%的有4个年份，相对误差小于0.5%的有21个年份。同时，95%置信区间相对于变量值而言也相对较小。综合这些情况，可以得出这样的结论：根据能源消费和经济结构变量的适当模型，能够比较好地模拟和预测GDP。

表3-6　基于能源与结构变量模型计算的GDP模拟值、相对误差与置信区间

图3-1反映了GDP统计增长率与依据公式（3-21）计算的模拟增长率。图3-1表明，1993年以前，GDP模拟增长率与统计增长率的拐点、峰点与谷点，除个别年份外，基本都在相同年份出现，只是模拟增长率延伸得更为远一点，因此从波动模式上看，模拟增长率与统计增长率并没有太大的区别。1993年以后，情况发生了很大的变化，GDP统计增长率相对更为平稳一些，变化更为缓慢一些，而模拟增长率则波动得较为严重，特别是1998年以后，相对于统计增长率，模拟增长率的波动更为频繁和剧烈。(www.xing528.com)

图3-1　GDP统计增长率与模拟增长率

三、GDP方差分解、脉冲响应与基于ARMA模型估计的GDP增长率

上面根据能源消费与经济结构对GDP的模拟，本质上是一种静态模拟。这种静态模拟只是显示了解释变量与被解释变量之间的相关性或因果性，没有解释变量微小变动、初始时间点选择的变动、相关系数的微小变动，通过其内在联系，对被解释变量及其他变量会产生什么影响，因而没有对被解释变量的稳定性做出任何说明。

首先，本部分利用VAR模型对实际GDP的对数、不包含电力的能源消费的对数、电力消费的对数以及第三产业增加值的对数等变量间的系统关系作进一步脉冲响应分析，试图发现各变量对其他不同变量脉冲扰动的短期和长期反应，进而发现各变量间的动态关系；其次，利用方差分解对各变量的不同预测期限的预测误差的方差进行分解，以便了解各信息对模型内生变量的相对重要性；最后，利用ARMA模型估计的GDP增长率的可信区间。

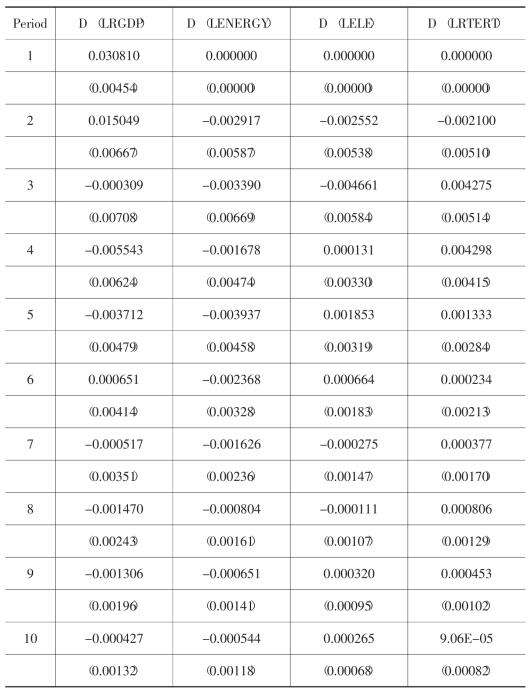
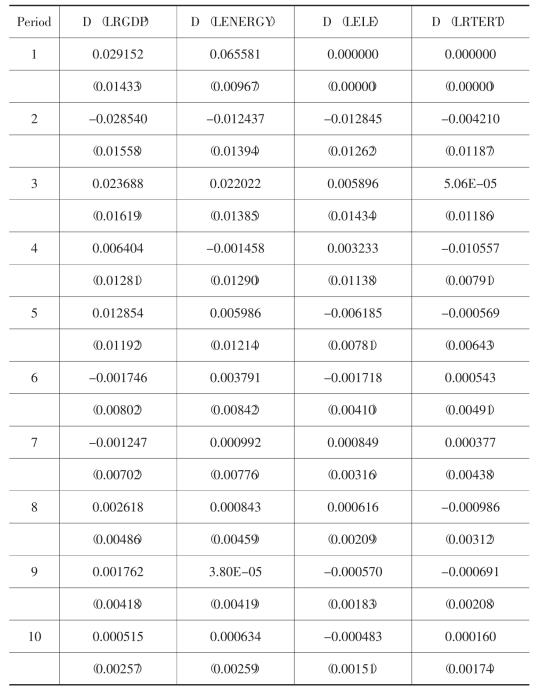
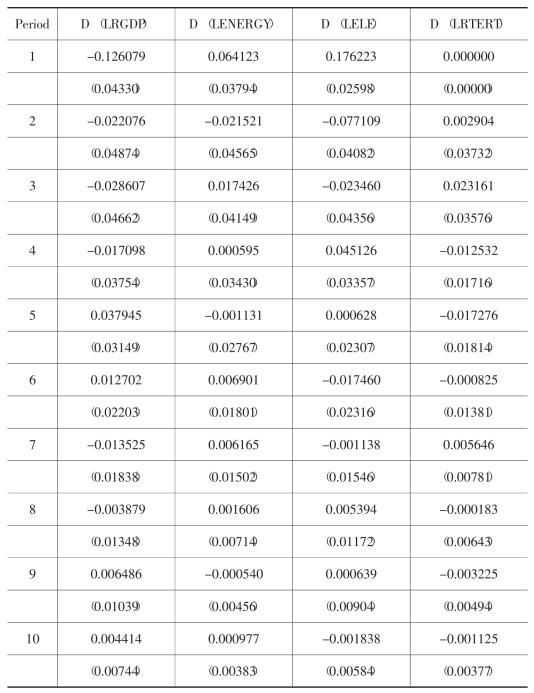
脉冲响应函数描述各内生变量对创新的一个单位标准差冲击对内生变量的当前值和未来值会产生多少影响。根据AIC和SC准则，脉冲响应函数的滞后期选取为2期，下面的脉冲图（图3-2a）显示了相应的计算结果。

脉冲图表明，实际GDP的对数对于其自身及电力、第三产业增加值的一个脉冲响应均为正，但持续时间不同。实际GDP的对数对于其自身一个脉冲响应开始上升，到第二期达到最大，然后开始减弱，第七期以后响应基本稳定；对于电力消费的一个脉冲响应到第五期时达到最大，然后基本稳定；对于第三产业的一个脉冲响应到第二期时达到最大，而后开始减弱。实际GDP的对数对于不含电力的能源消费的一个脉冲响应开始时为负，第二期开始上升，并迅速转为不断增强的正的响应，第七期以后基本稳定。

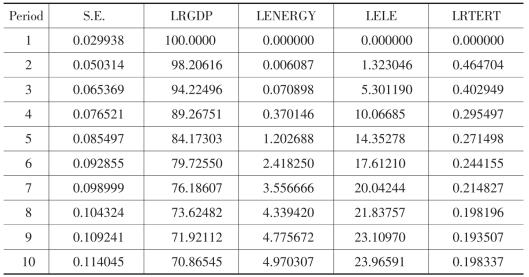
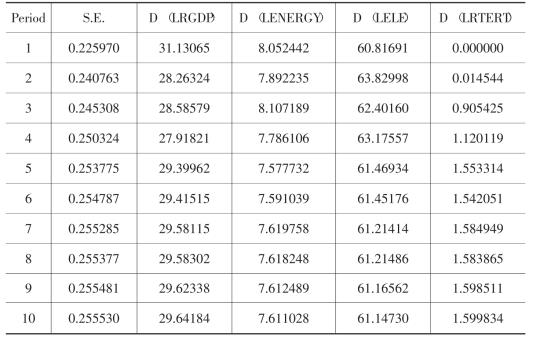
图3-2b给出了实际GDP对数的方差分解结果。图3-2b中曲线表明，GDP的观测误差主要是由自身扰动引起的。虽然这种扰动的影响强度在下降，但下降幅度很小，从初始时期的100%到第十期时仍然有70%。不含电力的能源消费对GDP预测误差的扰动到第五期时才超过1%，从第八期开始基本稳定在4%～5%的水平上。电力消费对GDP预测误差的扰动相对较大，而且跳跃性很大，从第二期的1.32%上升到第三期的5.30%，再上升到第四期的10%，第七期以后基本稳定在20%～25%的水平上。第三产业对GDP预测误差的扰动相对很小，从第二期的0.46%持续下降到第八期的0.198%。

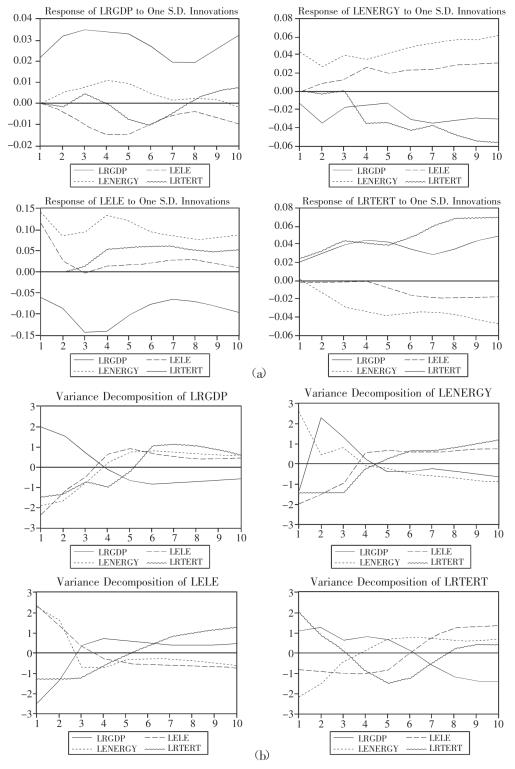
图3-2　实际GDP的脉冲响应与方差分解图

不论是从脉冲响应函数还是从GDP预测误差方差分解的角度看，上述结果都表明，典型省GDP序列自身具有很强的鲁棒性（robustness）或一致性（consistency）。这种鲁棒性或一致性表明，若从GDP序列自身构造预测模型，可能会得到预测更为精细的结果。因此，我们根据Hendry的模型构造原则，并根据AIC和SC准则，确定了如表3-7所示的自回归移动平均模型。

表3-7　自回归移动平均模型

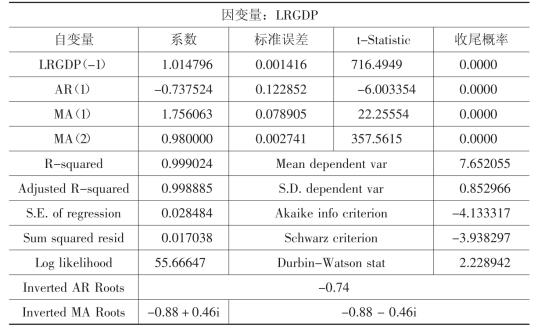
表3-7表明，自回归移动平均模型各变量的收尾概率均为0.0000，因此，在统计上极为显著，调整的判决系数为0.999，说明该模型解释了GDP变差的99.9%，滞后一期的GDP系数大于1，反映了样本期间GDP增长率不断上升这一事实。根据上述自回归移动平均模型，我们计算了各个年份的模拟值、实际值与模拟值之间的相对误差、依模拟值计算的GDP增长率、统计增长率与模拟增长率之间的绝对误差，以及实际GDP对数的95%置信区间（见表3-8）。同时，为了进行对比，给出了GDP统计增长率与模拟增长率的曲线图（见图3-3）。

图3-3　GDP统计增长率、ARMA模拟增长率与基于能源与结构变量模型的模拟增长率（%）

计算结果表现出了如下特征：

（1）GDP统计值与模拟值之间相对误差在0.5%以上的有1983年、1987年、1988年和1993年4个年份，其中1987年相对误差最大，达到0.91%；误差在0.3%～0.5%之间的有5个年份；误差在0.1%～0.3%之间的有11个年份；误差小于1%的有6个年份；误差为正的有12个年份；误差为负的有14个年份。1990年以后，GDP统计值大于模拟值较为明显的有1991年（0.21%）、1992年（0.49%）和1993年（0.51%）；GDP统计值小于模拟值较为明显的有1999年（-0.38%）和2001年（-0.42%）。

（2）GDP统计增长率与模拟增长率之间绝对误差超过5个百分点的有1987年、1988年、1994年、2001年和2002年5个年份；误差在2～5个百分点之间的有9个年份；误差在1～2个百分点的有7个年份；误差小于1个百分点的有4个年份；误差为正的有15个年份；误差为负的有10个年份。1990年以前，GDP统计增长率与模拟增长率差别较大的有1983年（2.62个百分点）、1985年（-3.58个百分点）、1986年（-2.06个百分点）、1987年（10.46个百分点）、1988年（-13.61个百分点）和1990年（3.78个百分点）；1990年以后，GDP统计增长率与模拟增长率差别较大的有1992年（2.47个百分点）、1994年（-5.51个百分点）、1995年（2.42个百分点）、1996年（-3.07个百分点）、1999～2002年（分别为-3.64、4.61、-5.23和5.24个百分点）。

表3-8　基于ARMA模型的GDP对数的模拟值、相对误差、增长率误差及95%置信区间

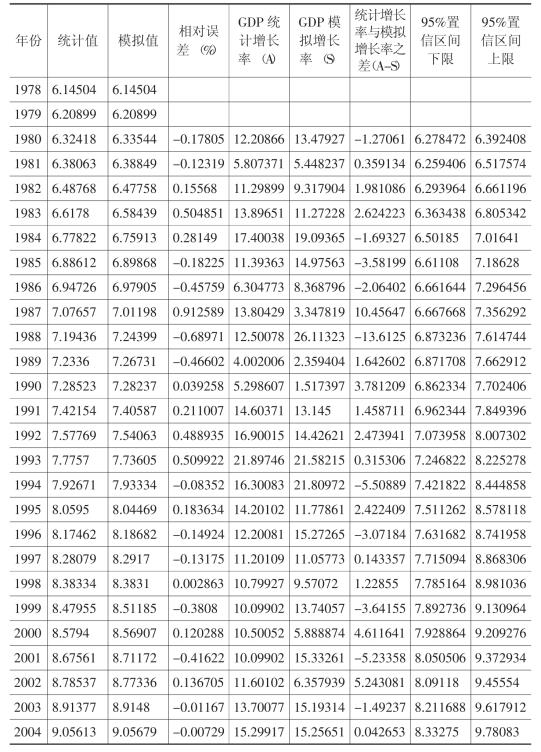
（3）1993年以后，GDP统计值与GDP模拟值、GDP统计增长率与模拟增长率，各自的平稳性出现较大的差别。GDP统计值与统计增长率，相对于GDP模拟值与模拟增长率，都要更平稳些，而后者的波动性较大。特别是1997～2002年期间，GDP统计增长率的首尾年份分别是11.2和11.6，中间年份的GDP统计增长率均在10～11之间波动，而此间的GDP模拟增长率却有较大幅度的波动，波动幅度最大时接近10（见表3-8及图3-3）。这种差别可以做出几种解释：一是模拟值的波动源于历史依赖性，因为GDP增长率序列在1993年以前存在着较大的波动性，由于惯性的作用，这种波动一直延伸；二是GDP统计增长率的平稳性来源于宏观调控政策，是近年来中国实施稳定经济政策的结果；三是GDP统计数据经过了加工和调整，消除了波动性。

（4）为了进一步理解基于ARMA模型模拟的GDP增长率的波动性，图3-3将GDP统计增长率、基于ARMA模型的GDP模拟增长率和基于能源与结构变量模型的GDP模拟增长率绘制在一起。图中清晰表明，两种模型模拟的GDP增长率具有基本相似的波动性，特别是2000年以后，拐点、峰点、谷点基本同步。由于基于能源与结构变量的模拟模型相对于ARMA模型而言，更具外生性，因此从这一点来看，GDP增长率具有一定的波动性，可能更为接近现实。

第五节　结　论

本书利用计量工具考察了典型省GDP与能源消费的关系，并通过构建结构模型和自回归移动平均模型模拟了GDP增长率，构建了GDP及其增长率的95%置信区间。实证研究结果表明：

（1）典型省能源消费总量与典型省GDP、农业增加值、第三产业增加值、工业增加值是协整的，即存在长期均衡关系，与第二产业增加值不是协整的；不包含电力的能源消费总量与GDP、农业增加值、第二产业和第三产业增加值以及工业增加值是协整的；电力消费与所有产出变量都不是协整的。

（2）典型省大部分产出变量与大部分能源消费变量之间存在单向的因果关系，即经济增长为能源消费的Granger原因。能源消费与经济增长之间关系的短期波动，主要是由于工业或第二产业产出水平与能源消费之间关系的波动引起的。

（3）第二产业产出水平对能源消费的影响随着产出水平的提高而增加，但这种增加是规模递减性的，第二产业产出水平的能源消费弹性具有先上升后下降的趋势，因而能源消费与第二产业产出水平的关系是一个非线性关系，进而表明能源消费与GDP的关系也是一个非线性关系，因此，从能源消费的线性变化中不能推出GDP的确切变化，因为能源消费不仅与GDP总量相关，而且与GDP的结构，即经济结构相关。

（4）包括能源变量非线性项和结构变量的模型能够较好地模拟和预测典型省GDP及其增长率。

（5）典型省GDP序列具有较强的鲁棒性或一致性，因而自回归移动平均模型能够较好地模拟和预测GDP及其增长率。1993年以后，两种模型模拟的GDP增长率相对于GDP统计增长率，具有更强烈的波动性。

（6）两种模型给出的模拟GDP与统计GDP之间的相对误差大多数是可接受的，但两种模型给出的GDP模拟增长率与统计增长率之间的绝对误差在某些年份超出了可接受的范围。两种模型给出的GDP及其增长率的95%置信区间都在可接受的范围之内。两种模型模拟的GDP及其增长率之间的相似性，超过了与统计GDP及其增长率的相似性。

（7）仅从两种模型显示的经济模拟增长率来看，典型省GDP统计增长率有高估的年份，也有低估的年份，综合影响基本相互抵消。因此，从长期来看，典型省GDP统计增长率平均数是可信的，但这只是一个暂时的结论，需要有更进一步的证据加以检验和支持，特别是需要与中国的总体状况及其他省份的状况加以对比后，才能确认这一结论的可信性。

参考文献

1.蔡、王美艳：《中国经济增长究竟有多快？》，《新视野》2002年第4期。

2.林伯强：《中国能源需求的经济计量分析》，《统计研究》2001年第10期。

3.林伯强：《电力消费与中国经济增长：基于生产函数的研究》，《管理世界》2003年第11期。

4.林伯强：《结构变化、效率改进与能源需求预测——以中国电力为例》，《经济研究》2003年第5期。

5 .马超群等：《中国能源消费与经济增长的协整与误差校正模型研究》，《系统工程》2004年第10期。

6.周建：《中国GDP及其增速可信度的小样本因果关系分析》，《河北经贸大学学报》2002年第5期。

7.赵宝珍：《提高统计数字质量问题研究》，《辽宁商专学报》1997年第2期。

8.刁恒昌等：《论统计数字的质量问题及其对策》，《黑龙江财专学报》1996年第2期。

9.李德水：《关于GDP的几点思考》，《经济研究》2004年第4期。

10.统计数字质量研究课题组：《在新旧体制转换过程中如何保证统计数字的准确性和及时性》，《统计研究》1995年第2期。

11.王金海：《更准、更快、更全：调正统计“晴雨表”》，《人民日报》1998年4月26日。

12.于洪彦、许松山：《论统计数字》，《吉林财贸学院学报》1990年第5期。

13.赵鹏：《农村经济统计不实的原因与对策》，《农村合作经济经营管理》1998年第6期。

14.王丕斌：《对我国经济增长率计算方法的看法》，《经济研究》1999年第4期。

15. Abuaf，N.，Jorion，P.，1990. Purchasing power parity in the long run. Journal of Finance 45，157-174.

16. Asafu-Adjaye，J.，2000. The relationship between energy consumption，energy prices and economic growth：time series evidence from Asian developing countries. Energy Economics 22，615-625.

17. Azali，M.，Habibullah，M.S.，Baharumshah，A.Z.，2001. Does PPP hold between Asian and Japanese economies？Evidence using panel unit root and panel cointegration. Japan and The World Economy 13，35- 50.

18. Banerjee，A.，Dolado，J.J.，Hendry，D.F. and Smith，G.W. 1986. Exploring Equilibrium Relationships in Econometrics Through Static Models：Some Monte Carlo Evidence. Oxford Bulletin of Economics and Statistics，48，253-277.

19. Basu，P.，Chakraborty，C.，Reagle，D.，2003. Liberalization，FDI，and growth in developing countries：a panel cointegration approach. Economic Inquiry 41（3），510- 516.

20. Canning，D.，Pedroni，P.，1999. Infrastructure and long -run economic growth. Mimeo. Indiana University.

21. Charemza，W.W. and Readman，D.F.（1997）New Directions in Econometric Practice：General to Specific Modelling，Cointegration and Vector Autoregression，2ndedn.，Cheltenham：Edward Elgar.

22. Dickey，D.A.，Jansen，D.W. and Thornton，D.L.（1994）‘A primer on cointegration with an application to money and income’，in B.B.Rao（ed.），Cointegration for the Applied Economist，New York：St. Martin’s Press.

23. Enders，W.（1995）Applied Econometric Time Series，New York：John Wiley.

24. Engle，R.，Granger，C.，1987. Cointegration and error correction：representation，estimation，and testing. Econometrica 55，257- 276.

25. Fatai，K.，Oxley，L.，Scrimgeour，F.G.，2004. Modelling the causal relationship between energy consumption and GDP in New Zealand，Australia，India，Indonesia，the Philippines and Thailand. Mathematics and Computers in Simulation 64，431- 445.

26. Glasure，Y.U.，Lee，A.R.，1997. Cointegration，error-correction，and the relationship between GDP and electricity：the case of South Korea and Singapore. Resource and Energy Economics 20，17-25.

27. Granger，C.W.J. and Newbold，P.，1974. Spurious Regressions in Econometrics. Journal of Econometrics，14，111-120.

28. Granger，C.W.J. and Newbold，P.，1988. Some Recent Developments in a concept of Causality. Journal of Econometrics，39，199-211.

29. Gujarati，D.N. 1995. Basic Econometrics，3rd edn.，New York：McGraw-Hill.

30. Hadri，K.，2000. Testing for stationarity in heterogeneous panel data. Econometrics Journal 3，148-161.

31. Holden，D. and perman，R. 1994. Unit roots and cointegration for the economist，in Rao，B.B.（ed.），Cointegration for the Applied Economist，New York：St. Martin’s Press.

32. Im，K.S.，Pesaran，M.H.，Shin，Y.，1997. Testing for unit roots in heterogeneous panels. Working Paper. University of Cambridge.

33. Johansen，S.，1988. Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control 12，231- 254.

34. Jumbe，C.，2004. Cointegration and causality between electricity consumption and GDP：empirical evidence from Malawi. Energy Economics 26，61-68.

35. Kraft，J.，Kraft，A.，1978. On the relationship between energy and GNP. Journal of Energy and Development 3，401- 403.

36. Lee，C.H.，Huang，B.N.，2002. The relationship between exports and economic growth in East Asian countries：a multivariate threshold autoregressive approach. Journal of Economic Development 27（2），45-68.

37. Levine，A.，Lin，C.F.，1993. Unit root tests in panel data：asymptotic and finite sample properties，Working Paper. Department of Economics，University of California at San Diego.

38. Levine，A.，Lin，C.F.，Chu，C.S.，2002. Unit root tests in panel data：asymptotic and finite -sample properties. Journal of Econometrics 108，1- 24.

39. MacKinnon，J.G.（1991）‘Critical values of cointegration tests’，in R.F. Engle and C.W.J. Granger（eds），Long-Run Economic Relationships：Readings in Cointegration，New York：Oxford University Press.

40. Masih，A.M.M.，Masih，R.，1996. Electricity consumption，real income and temporal causality：results from a multi-country study based on cointegration and error correction modeling techniques. Energy Economics 18，165-183.

41. Masih，A.M.M.，Masih，R.，1998. A multivariate cointegrated modeling approach in testing temporal causality between energy consumption，real income and prices with an application to two Asian LDCs. Applied Economics 30（10），1287-1298.

42. Morimoto，R.，Hope，C.，2004. The impact of electricity supply on economic growth in Sri Lanka. Energy Economics 26，77-85.

43. Nelson，C.R. and Plosser，C.I. 1982. Trends and Random Walks in Macroeconomic Time Series：Some Evidence and Implications. Journal of Monetary Economics，10，139-162.

44. Newey，W.，West，K.，1987. A simple positive semi -definite，heteroskedasticityandautocorrelationconsistentcovariancematrix. Econometrica 69（6），1519- 1554.

45. Oh，W.，Lee，K.，2004. Causal relationship between energy consumption and GDP revisited：the case of Korea 1970 -1999. Energy Economics 26，51-59.

46. Paul，S.，Bhattacharya，R.N.，2004. Causality between energy consumption and economic growth in India：a note on conflicting results. Energy Economics 26，977-983.

47. Pedroni，P.，1999. Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxford Bulletin of Economics and Statistics 61，653-670.

48. Pedroni，P.，2000. Full modified OLS for heterogeneous cointegrated panels. Nonstationary Panels Panel Cointegration and Dynamic Panels，Advances in Econometrics，vol. 15. JAI Press，pp. 93-130.

49. Phillips，P. and Perron，P. 1988. Testing for a unit root in time series regression. Biometica，75，335-346.

50. Pierse，R.G.，Shell，A.J.，1995. Temporal aggregation and the power of tests for unit root. Journal of Econometrics 65，335-345.

51. Rawski，T. 1993，“How fast has Chinese Industry Growth？”The World Bank Working Paper，WPS 1994.

52. Rawski，Thomas G.，2001a. China By the Numbers：How Reform Has Affected China’s Economic Statistics. China Perspectives，no. 33 （January-February），pp. 25-34（also available from www.pitt.edu/~tgrawski/papers2000）.

53. Rawski，Thomas G.，2001b. China’s GDP Statistics：A Case of Caveat Lector？available from www.pitt.edu/~tgrawski/papers2001；abbreviated version published as“The Credibility Gap：China’s Recent GDP Statistics，”China Economic Quarterly 5.1：18-22.

54. Sharma，S.C.，Dhakal，D.，1994. Causal analyses between exports and economic growth in developing countries. Applied Economics 26，1145-1157.

55. Soytas，U.，Sari，R.，2003. Energy consumption and GDP：causality relationship in G -7 countries and emerging markets. Energy Economics 25，33-37.

56. Stern，D.I.，1993. Energy and economic growth in the USA. Energy Economics 15，137- 150.

57. Stern，D.I.，2000. Multivariate cointegration analysis of the role of energy in the US macroeconomy. Energy Economics 22，267- 283.

58. Stock，J.H. 1987. Asymptotic properties of least squares estimators of cointegrating vectors. Econometric，55，1035-1056.

59. Toda，H.Y.，Yamamoto，T.，1995. Statistical inference in vector autoregressions with possible integrated processes. Journal of Econometrics 66，225-250.

60. WDI，2004. World Development Indictors. World Bank.

61. Yang，H.，2000. A note on the causal relationship between energy and GDP in Taiwan. Energy Economics 22（3），309-317.

62. Yu，S.H.，Choi，J.Y.，1985. The causal relationship between energy and GNP：an international comparison. Journal of Energy and Development 10，249- 272.

附表：各变量预测误差方差分解与脉冲响应

Variance Decomposition of LRGDP：

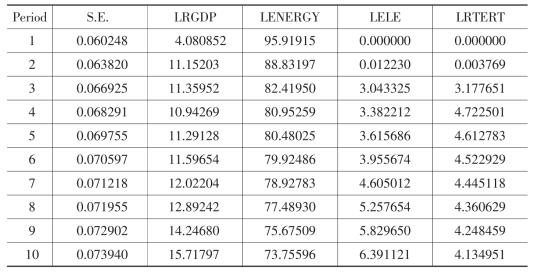
Variance Decomposition of LENERGY：

Variance Decomposition of LELE：

Variance Decomposition of LRTERT：

Impulse response to one S.D. innovation

Response of LRGDP：

Response of LENERGY：

Response of LELE：

Response of LRTERT：

Variance Decomposition of D（LRGDP）：

Variance Decomposition of D（LENERGY）：

Variance Decomposition of D（LELE）：

Variance Decomposition of D（LRTERT）：

Impulse response of one S. D. innovation

Response of D（LRGDP）：

Response of D（LENERGY）：

Response of D（LELE）：

Response of D（LRTERT）：