供应链环境下的客户知识协同获取激励机制研究

6　双边道德风险下基于关系契约的客户知识协同获取激励机制

6.1　引　言

第5章研究了制造商与销售商协同获取客户知识中由信息不对称引起的双边道德风险，并设计了一个双边激励契约降低道德风险并实现合作双方的最优激励。本章进一步从关系契约角度对双边道德风险问题进行研究。

正如前文所述，客户知识不同于实物产品，它具有无形性、转移黏滞性的特点，其获取（包括利用）更多地依赖于知识本身的特性、个体与组织的学习能力及环境。供应链中制造商与销售商拥有的客户知识、人才等资源及其学习能力的不平衡导致了他们在知识合作中存在投机行为，这引发了双边道德风险问题（Garcia，2002）。双边道德风险使得制造商与销售商在知识合作中投入不足，客户知识协同获取的成功率较低。

销售商处于供应链下游掌握了大量的客户数据，要将这些数据转化为有用的客户知识，要求具备较强的人力与技术资源，需要付出较大的成本，面临这一问题，销售商可选择的一个有效解决途径是与制造商合作，利用制造商拥有的人才与技术实现客户知识获取。然而，作为理性经济人，销售商一方面希望利用制造商的资源来解决人才、技术与成本问题；另一方面，又不愿共享过多的客户数据。针对销售商的矛盾心理，制造商的一个有效措施是在客户知识合作获取中设计合理的激励机制。然而，制造商由于拥有技术与研发人员优势，对客户知识获取后的创新成果和收益信息也不愿意过多地与销售商分享，因此，在契约的设计中也要考虑对制造商的激励以降低其投机行为。人们对激励机制建模研究中大量的正式契约设计研究表明，在满足预算约束平衡条件下，不存在一种分配机制能激励合作参与者的努力水平达到系统最优（Holmstrom，1982；Corbett，2005），因而，精心设计的正式契约往往难以达到预期的激励效果。于是，长期的关系激励契约被提出来解决这一问题。关系契约激励模型的早期代表性文献侧重研究了企业内部雇佣关系激励与企业外包关系激励契约问题（Baker，2002）。其后，有文献对研发外包中的关系激励进行了进一步研究（王安宇和司春林，2006），有文献利用关系契约对公司治理中参与人的心理因素及监督影响下动态激励进行了研究（Sloof，2011），有文献将激励分为显性与隐性并研究了显性激励与关系激励的交互作用（庄新田和王健，2010），但尚未见到有文献从客户知识获取的角度对制造商与销售商合作中的关系激励机制进行研究。鉴于此，本书将考虑客户知识获取的特点，基于关系契约建立数学模型对制造商与销售商合作中的努力、激励以及效率问题进行研究。

本章的主要内容如下:第6.2节是问题描述和模型假设；第6.3节是正式契约下客户知识协同获取合作模型；第6.4节是关系契约下客户致死协同获取合作模型；第6.5节是本章小结。

6.2　问题描述与模型假设

在客户知识获取的过程中，销售商从与客户的直接交易与接触中获取了大量的客户数据、信息，而从这些数据和信息中获取客户知识是一项复杂的工程，仅仅依靠销售商的力量将这些数据、信息转化为有用的客户知识比较困难（Bucklin，1999）。因为完成这项工作要求具备较强的人力与技术资源，需要付出较为高昂的成本（Lilien，2004）。面临这一问题，从销售商的角度看，销售商可选择的一个有效解决途径是与制造商合作，利用制造商拥有的人才与技术实现客户知识获取；从制造商的角度看，与销售商合作无疑可以获得大量的一手客户资料，降低了它获取客户数据的成本，因此，双方都有合作的意愿。基于这个意愿，双方就客户知识获取进行合作。典型的例子如沃尔玛就其饰品的设计、选材、生产到销售环节与其制造商进行基于客户知识的合作。首先，销售商向制造商转移自己拥有的客户数据、信息和知识，由于客户知识具有转移黏滞性，销售商必须参与并努力配合才能促使知识流动顺畅，此时，制造商也要付出努力吸收、内化从销售商处获得的客户知识；制造商在获得这些知识后将其应用于设计研发或生产、营销等环节，并在这个过程中创造出了有关客户的新知识，为了促进新产品的销售，制造商将有关客户的新知识向销售商转移，这时，制造商须付出努力克服黏滞性，而销售商也须参与并付出努力促进新知识的转移。由此可见，在客户知识获取的整个过程中，合作双方生产要素投入表现为知识、技术和人力资源等，双方基于这些资源建立合作生产关系（Szulanski，1996；李双燕和万迪昉，2008）。然而，作为理性经济人，销售商一方面希望利用制造商的资源来解决人才、技术与成本问题；另一方面，又不愿共享过多的客户数据与信息。针对销售商的矛盾心理，制造商的一个有效措施是在客户知识合作获取中设计合理的激励机制。同时，制造商由于拥有技术与研发人员优势，对客户知识获取后的创新成果和收益信息也不愿意过多地与销售商分享，因此，在契约的设计中考虑双边道德风险。在双边道德风险下，由于知识黏性以及知识、技术与人力资源具有不易观察量化的特性，销售商和制造商在合作过程中都可能出现败德行为。为了进一步对双边道德风险下的契约激励进行研究，现作如下假设。

假设1　假设制造商倡导合作，提出合作契约，销售商参与合作付出的努力水平为e，由于销售商在合作中积极性及配合程度受到e的影响，因此，销售商参与合作的配合度以概率f（e）表示，其中0≤e≤1，f（e）满足＞0，＜0，表示销售商参与客户知识合作获取的配合度随其努力e的增加而提高，变化速度随着e变化速度的递增而递减，这满足边际递减规律；且f（e）为凹函数。

假设2　假设客户知识合作获取过程中知识黏性受制造商与销售商努力的影响，设知识黏性系数为双方努力的函数μ（a，e），其中a表示制造商付出的努力水平，其中，0＜μ（a，e）＜1^[1]。为简化模型便于研究，假设θ（a，e）＝1－μ（a，e），其中θ（a，e）为客户知识合作获取的容易程度，且满足

＞0，＜0，表明制造商与销售商合作过程中，客户知识获取的黏性随制造商的努力a、销售商的努力e的增加而降低，黏性系数的变化速度随着a，e变化速度的递增而递减，满足边际递减规律；且有θ（a，e）为凹函数，0＜θ（a，e）＜1。

假设3　假设制造商与销售商合作过程中付出的成本分别为c（a），c（e），且满足成本递增和边际递增规律，＞0。

假设4　制造商与销售商均为风险中性。结合本书研究的问题及假设，并参考霍姆斯特姆与米尔格罗姆参数化扩张模型，假定制造商激励销售商参与的支付函数为ω＝α＋βyθ（a，e）f（I，e），其中，α表示销售商参与合作时，制造商给出的固定支付，β表示合作成功时销售商分享的产出份额，即收入共享激励系数，β∈［0，1］；yθ（a，e）f（e）表示合作成功时获得的产出，记为π，其中，θ（a，e）f（e）表示合作成功的概率，y表示合作成功获得的理想产出。

假设5　制造商和销售商均为风险中性，双方参与客户知识合作获取付出的努力程度均不易观察，即制造商的努力a、销售商的努力e均为各自的私人信息。

6.3　基于正式契约的激励模型

正式契约是指承诺在事前是明确的，事后可验证的，并且它可由第三方（如法庭）强制实施的一次性静态契约（张维迎，1996）。本书中制造商和销售商的工作努力程度a，e属于私人信息，难以被第三方验证，不能作为一种承诺写入契约，因此，有效契约只能由销售商参与情况下的固定支付费用α和合作成功时制造商奖励销售商的产出份额β构成支付契约。正式契约下，制造商与销售商进行单周期的两阶段博弈，博弈过程如下:第一阶段，制造商设计激励契约，第二阶段制造商和销售商分别确定自己的努力水平。

根据前述假设和分析可知制造商与销售商协同获取客户知识的期望收益函数分别为

针对上述模型，采用逆向归纳法求解。首先，给定激励契约，求解第二阶段制造商与销售商的努力投入。

第二阶段，销售商的问题是如何决策在客户知识合作获取中投入的努力水平，从而使得自身收益最大化:

对e求（6.3）式的一阶条件可得

同理，制造商的问题是在客户知识合作获取中如何决策自己的努力水平使自身收益最大化:

对a求（6.5）式的一阶条件

由式（6.4）和式（6.6）联合求解，可得给定激励契约时博弈第二阶段制造商与销售商工作努力水平的均衡解。考虑双边道德风险，博弈第一阶段制造商进行激励契约设计，可用如下优化问题P1描述:P1

其中，式（6.7）为制造商收入目标函数，式（6.8）为制造商的激励相容约束，式（6.9）为销售商的激励相容约束，式（6.10）为销售商参与客户知识协同获取的参与约束，其中 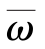表示销售商参与合作的保留效用，即参与合作后销售商至少能获得 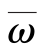的收入。

由于式（6.10）取等号为销售商参与协同合作的最低约束条件。对制造商而言，为了保证自己的收益最大，将选择满足销售商的最低要求。因此，由式（6.10）取等号可得:

式（6.11）代入式（6.7），可得:

注意到式（6.12）中S（a，e）＝yθ（a，e）f（e）－c（a）－c（e）为制造商与销售商合作获取客户知识的系统收益，因此，原问题P1可重新表示为P2:P2

由前述假设和分析可知，上述优化问题P2中式（6.13）即制造商的收入目标函数为凹函数，约束条件式（6.14）、式（6.15）有最优解，因此，可求得问题P2的最优解为（β∗，a∗，e∗）。

进一步分析P2可得如下命题。

引理6.1　正式契约下，有β∈（0，1），即制造商必须给出一定的激励才能促使销售商参与客户知识协同获取并付出努力促进合作成功；制造商必须参与收益分享，否则退出合作。

证明:有假设可知＞0，当β＝0时，销售商的激励相容式（6.15）不成立，当β＝1时，制造商的激励相容式（6.14）不成立，因此，客户知识协同获取的产出必须被分享，一方面制造商要拿出一定比例的产出来激励销售商努力，另一方面，制造商也要保留一部分产出来维持合作（即对自己的激励）。鉴于此，双方在正式契约下合作时，有β∈（0，1）。得证。

引理6.2　表明正式契约下，促进制造商与销售商的客户知识获取合作成功的一个重要条件是获取的收益必须被分享，同时，双方对合作的风险进行分担。

命题6.1　正式契约下，a∗＜as，e∗＜es，θ∗＜θs，即制造商与销售商的最优努力水平低于系统最优时的努力水平，客户知识获取的知识黏性大于系统收益最优时的知识黏性。

证明:若制造商与销售商组成一个系统进行集中决策，则客户知识协同获取的系统期望收益为:

由前述假设和分析易知式（6.16）为凹函数，有最优解，令系统收益最大化时制造商的最优努力为as，销售商的最优努力水平为es，则as，es满足如下一阶条件:

比较式（6.17）与（6.18）的左边，若a∗＝as则有:

显然，若式（6.19）成立，则β＝1。同理可证，若e∗＝es，式（6.15）与式（6.18）的左边相等，β＝0，这与引理1中β∈（0，1）矛盾，因此，a∗≠as，e∗≠es。(www.xing528.com)

进一步由式（6.16）可以推导出:

由假设可知，f（e）≥0，＞0，则式（6.20）＜0，因此，式（6.19）在a∈［0，1］上是凹函数，在a＝as处存在最大值，即在这个点上系统收益最大；由式（6.19）在a∈［0，1］上的性质可知，存在a1∈［0，as］，a2∈［as，1］使得s（a1）＝s（a2）。由于制造商是理性的，其努力水平必然会落在［0，as］上，由于a∗≠as，因此可得a∗＜as；同理可证得e∗＜es。

由于θ（a，e）在［0，1］上为凹增函数，且根据上述证明，a∗＜as，e∗＜es，因此，易证得θ∗＜θs。

证毕。

命题6.1表明制造商设计的最优正式契约不能使双方在合作过程中投入的努力水平及知识黏性系数达到系统最优，导致了系统利润受损。

6.4　基于关系契约的激励模型

区别于正式契约的单次、静态、强制执行性，关系契约是基于长期持续关系的、动态的、非正式的契约，其主要特点是具有较好的“自我执行性”（Daido，2006）。由于制造商与销售商通常具有长期的合作关系，下面的研究企图基于关系契约建立制造商与销售商协同获取客户知识的优化模型以期降低合作中的知识黏性，提高合作效率。关系契约下，制造商在客户知识获取合作中承诺付出努力୺a，此时，销售商判断制造商的承诺是否可信，即制造商的承诺是否有“自我执行性”，若可信，销售商则根据制造商给出的关系契约୿ω＝୺α＋୺βyθ（୺a，୵e）f（୵e）选择使自己收益最大化的努力水平୵e；若判断制造商的承诺是不可信，销售商将拒绝关系契约，而缔结前文的正式契约。制造商与销售商的客户知识获取合作过程为两阶段博弈:第一阶段，制造商给出关系契约；第二阶段，销售商判断关系契约是否具有“自我执行性”，然后据此决策自己的努力水平。

针对两阶段博弈，采用逆向归纳法求解。销售商首先判断制造商给出的契约是否具有“自我执行性”。由于在客户知识获取的合作中，“自我执行性”取决于制造商守约的长期收益是否大于违约的长期收益。给定激励契约୿ω及制造商的努力水平୺a，销售商的决策问题如下:

对୵e求式（6.21）的一阶条件:

当制造商观察到销售商付出了最优努力，采取机会主义行为追求短期收益最大化从而违约，此时，制造商的决策是使得当期收益最大化。

求解上述问题可得制造商当期最优努力水平，记为୶a。

当销售商观察到制造商违约，那么以后各期都只会与制造商缔结正式契约。根据上一节正式契约的分析制造商以后各期的期望收益为yθ（a∗，e∗）f（e∗）－c（a∗）－c（e∗）－୻ω，令i为收益贴现因子（0≤i≤1），则制造商违约的期望净收益为:

若制造商遵守关系契约，则当期和以后各期的努力水平均为୺a，因此，制造商守约的期望净收益为:

博弈第一阶段，制造商进行关系契约设计，其最优化问题P3如下:P3

上述问题中，式（6.27）是关系契约下制造商的目标收益函数，式（6.28）是销售商的参与约束，式（6.29）是制造商在关系契约下的“自我执行”约束，式（6.30）是制造商的参与约束，式（6.31）是销售商的激励相容约束。

由于式（6.28）取等号为销售商参与合作的最低约束条件。对制造商而言，为了保证自己的收益最大，将选择满足销售商的最低要求。因此，将式（6.28）取等号代入式（6.27）、式（6.29）并化简可得P4。P4

由式（6.32）可知，关系契约下，系统收益最优时制造商获得最大收益，因此有୺a∗＝as。比较式（6.35）与式（6.28）可得୺β∗＝1时销售商获得关系契约下的最优收益，因此，存在最优努力水平୵e∗，且有୵e∗＝es。

由上述分析可得命题6.2。

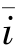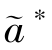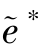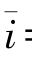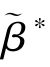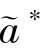命题6.2　关系契约下，收益贴现因子i对制造商和销售商的客户知识协同获取的效率有重要影响:①i∈［ୱ，1］时，制造商付出最优努力水平 ，销售商付出最优努力水平 ，此时ୱ＝c（as）/［s（as，es）－s（a∗，e∗）＋c（as）］。②若i＝0，存在一组解 ＝β∗，＝a∗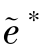，＝e∗使得关系契约退化为正式契约。③最优关系契约下，客户收益、系统收益为贴现因子i的非减函数。

证明:

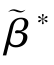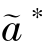①最优关系契约下有 ＝1，＝as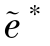，＝es，此时，制造商若选择违约最大化当期收益，则有 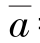＝0，将上述参数值代入式（6.33），可得:

由式（6.34）可知i＝c（as）/［s（as，es）－s（a∗，e∗）＋c（as）］为制造商“自我执行”契约的临界值，且由命题1可知s（as，es）≥s（a∗，e∗），因此，i≤1。

②若i＝0，则制造商与销售商只获得当期收益，此时的优化问题如P5。P5

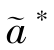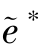比较P2和P5，P5多一个约束条件式（6.39），若要两个问题的解相同，则需P5中式（6.39）成立。假设两个问题有相同的解，即有 ＝a∗，＝e∗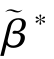，＝β∗，显然有s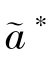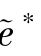（，）＝s（a∗，e∗），式（6.39）中的等式成立。②得证。

③令 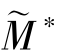＝s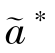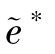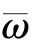（，）－为优化问题P4最优下的制造商收益，对P4构建拉格朗日函数，则有:

根据包络定理得

。由式（6.34），s（୺a，୵e）≥s（a∗，e∗），因此≥0，即最优关系契约下制造商收益是贴现因子的非减函数。注意到关系契约下系统收益与客户收益函数仅相差一个常数୻ω，因此，可推断系统收益也是贴现因子的非减函数。③得证。

由命题6.2可知，在关系契约下，收益贴现因子对制造商和销售商的客户知识协同获取效率有重要影响。若贴现因子很小，处于等于零的极端值时会使得关系契约退化为正式契约，即双方合作的效率降低；若贴现因子处于区间i∈［0，ୱi］时，随着i的增大，制造商的收益和系统收益随之增加。若贴现因子足够大，处于一定区间i∈［ୱi，1］时，参与双方付出最优努力水平，实现系统收益最优。这表明关系契约的设计必须考虑客户知识合作获取的长期收益，不仅关注当期收益，更要关注未来收益，从而激励制造商和销售商共同努力，提高合作效率，获得最优的客户知识获取效果。

命题6.3　比较正式契约与关系契约，在最优状态下，①关系契约下制造商与销售商的努力水平均大于正式契约下双方的努力水平，即存在 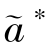＞a∗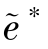，＞e∗；②关系契约降低了制造商与销售商协同获取客户知识过程中的知识黏性，促进了双方的合作，即有θ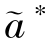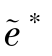（，）＞θ（a∗，e∗）；③关系契约下制造商的最优收益、系统最优收益均不小于正式契约下的制造商收益与系统收益。

证明:①由命题6.3有a∗＜as，e∗＜es，而根据优化问题P4可知，最优关系契约下（此时，i∈［ୱi，1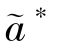］），＝as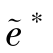，＝es，因此，在最优状态下存在a∗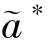＜，e∗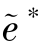＜。得证。②根据前文假设θ（a，e）为凹增函数，且制造商与销售商均为理性经济人，因此，基于①成立的情况下，显然有θ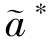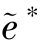（，）＞θ（a∗，e∗）。得证。③由命题6.2可知，i＝0时，关系契约退化为正式契约，且最优关系契约下，客户收益、系统收益为贴现因子i的非减函数，因此，最优关系契约下的制造商收益与系统收益均不小于最优正式契约下的制造商收益与系统收益。得证。

命题6.3表明，在客户知识获取的合作中，关系契约能够激励参与双方付出最优努力（当i∈［ୱi，1］时，有 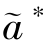＞a∗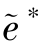，＞e∗）；能够降低客户知识获取过程中的知识黏性，促进双方的合作，从而提高双方乃至系统收益。因此，在设计激励机制时，制造商应从长远利益出发，通过建立长期的战略合作伙伴关系，从而激励销售商积极参与客户知识获取，付出最优努力水平，最终促进双方合作成功，获得较高的收益，实现双赢。

6.5　本章小结

本书通过建立基于关系契约的激励模型研究了制造商与销售商协同获取客户知识的激励机制，研究表明:最优正式契约不能使双方在合作过程中投入的努力水平及知识黏性系数达到系统最优，导致了系统利润受损；而从长远合作关系出发设计的关系契约激励机制对制造商与销售商的知识协同具有正向激励作用，能够降低知识协同获取的难度、提高知识协同获取效率，其中，收益贴现因子i对双方合作效率有重要影响，当它足够大达到一定临界值时，关系契约激励机制下的客户知识协同获取收益达到系统最优。

【注释】

[1]μ（a，e）＝0表示客户知识合作获取的理想状态，不存在任何阻碍，极容易合作获取，因此，不存在激励问题，若μ（a，e）＝1，知识黏性系数极大，难以转移，不易合作获取，因此，上述两种极端情况，不列入本书讨论的范围。