变革型领导与团队绩效关系的研究

§4.4　测量模型的验证与选择

前面通过内部一致性检验，将个体数据转化到团队层面，并进行了探索性因子分析，结果显示所设计的问卷具有很好的结构效度。在此，运用LISREL8.80软件对变革型领导、团队学习与团队绩效的测量模型进行验证，并通过比较一阶模型与二阶模型的拟合情况，选择最终模型。

4.4.1　变革型领导

根据前人的研究以及探索性因子分析的结果，本研究变革型领导包含了德行垂范、愿景激励、个性化关怀和领导魅力4个因子及26个指标。本研究运用LISREL8.80软件对变革型领导进行一阶验证性因子分析与二阶验证性因子分析，输出的变革型领导二阶与一阶验证性因子分析结果如图4-1、图4-2所示(需说明的是，由于在LISREL8.80软件中，变量允许的最大字符为8个字节，因此图中变革领导是指变革型领导，个性关怀即个性化关怀)。

4.4.1.1　模型拟合评价

在选择最终测量模型时，首先需要对经过验证性因子分析的模型进行评价，然后比较各模型的拟合情况。目前对模型的评价还没有形成统一的标准，通过大量阅读结构方程模型的文献发现，对模型的评价一般采用绝对指数、相对指数和简约指数这三类指数。为了科学合理地评估模型的拟合程度，本研究在这三类指数中分别选取学者们常用的指数作为评价模型拟合的标准，分别是:①卡方与自由度的比值(χ/df);②标准化残差均方根指数(SRMR);③赋范模拟指数(NFI);④非范模拟指数(NNFI);⑤比较拟合指数(CFI);⑥拟合优度(GFI);⑦近似误差均方根(RMSEA)。各拟合指数的评判标准如表4-10所示。

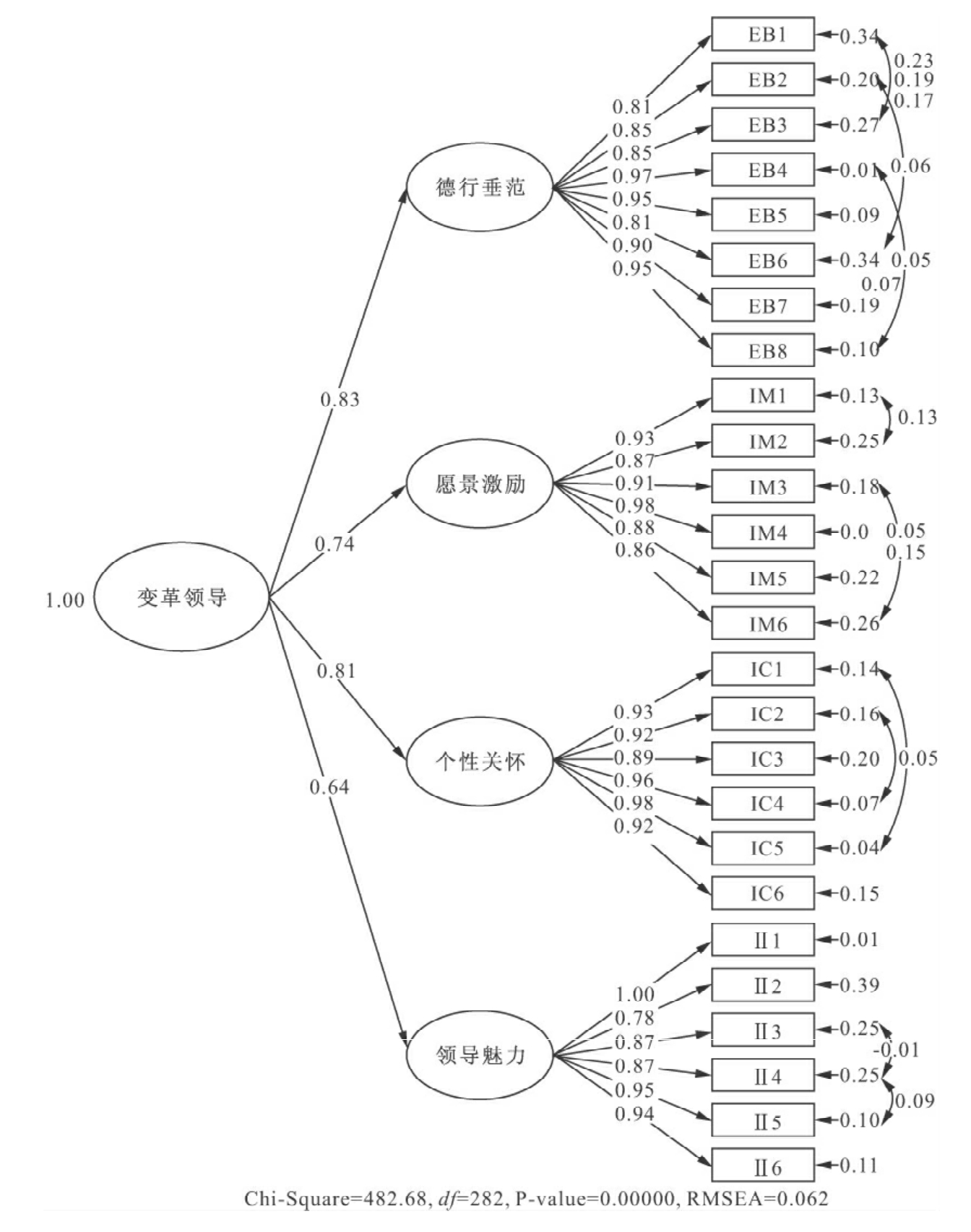
图4-1　变革型领导二阶验证性因子分析

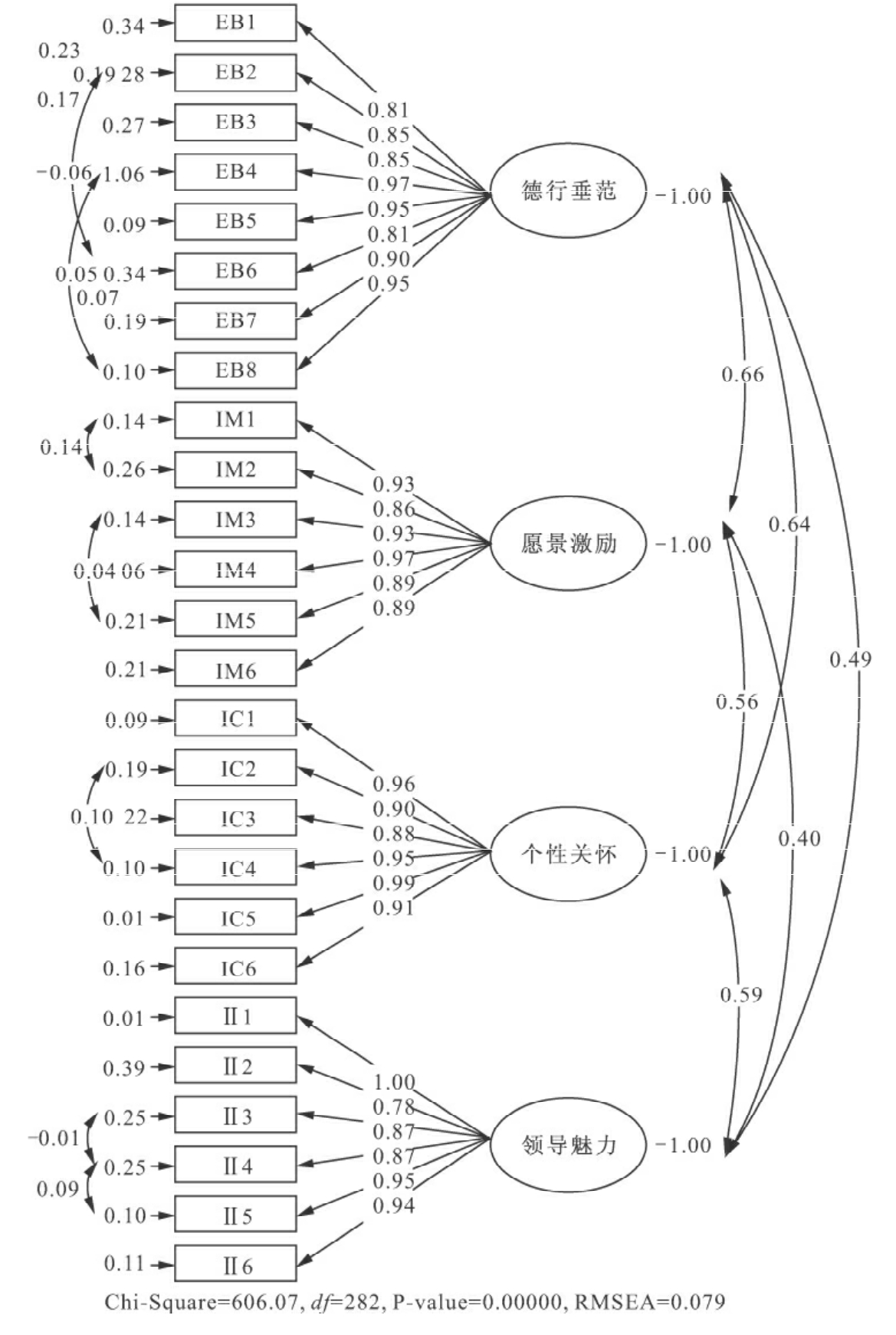
图4-2　变革型领导一阶验证性因子分析

表4-10　模型拟合评价指数参考值

根据变革型领导二阶验证性因子分析的结果分析报告，变革型领导二阶测量模型的拟合指标值如表4-11所示。

表4-11　变革型领导二阶测量模型拟合评价指数

根据变革型领导一阶验证性因子分析的结果分析报告，变革型领导一阶测量模型的拟合指标值如表4-12所示。

表4-12　变革型领导一阶测量模型拟合评价指数

由表4-11和表4-12可以看出，变革型领导的二阶测量模型与一阶测量模型的拟合情况均达到标准，拟合情况良好。若将两个测量模型的拟合情况进行比较，二阶测量模型的拟合情况要优于一阶测量模型。从理论上分析，变革型领导包含了德行垂范、愿景激励、个性化关怀与领导魅力四个维度，也就是说德行垂范、愿景激励、个性化关怀与领导魅力4个初阶因子受到一个共同的高阶因子变革型领导所决定。无论是从理论分析还是模型的实证检验，二阶模型都要优于一阶模型。在本研究中，我们采用变革型领导的二阶测量模型作为最终的模型。同时，采用二阶测量模型可以将初阶因子通过组合分数简化成观察变量，将二阶测量模型降级成一阶测量模型，这样可以减低测量模式的复杂度，提高模式的简效性，有利于解释潜在因子之间的关系。

4.4.1.2　信度检验

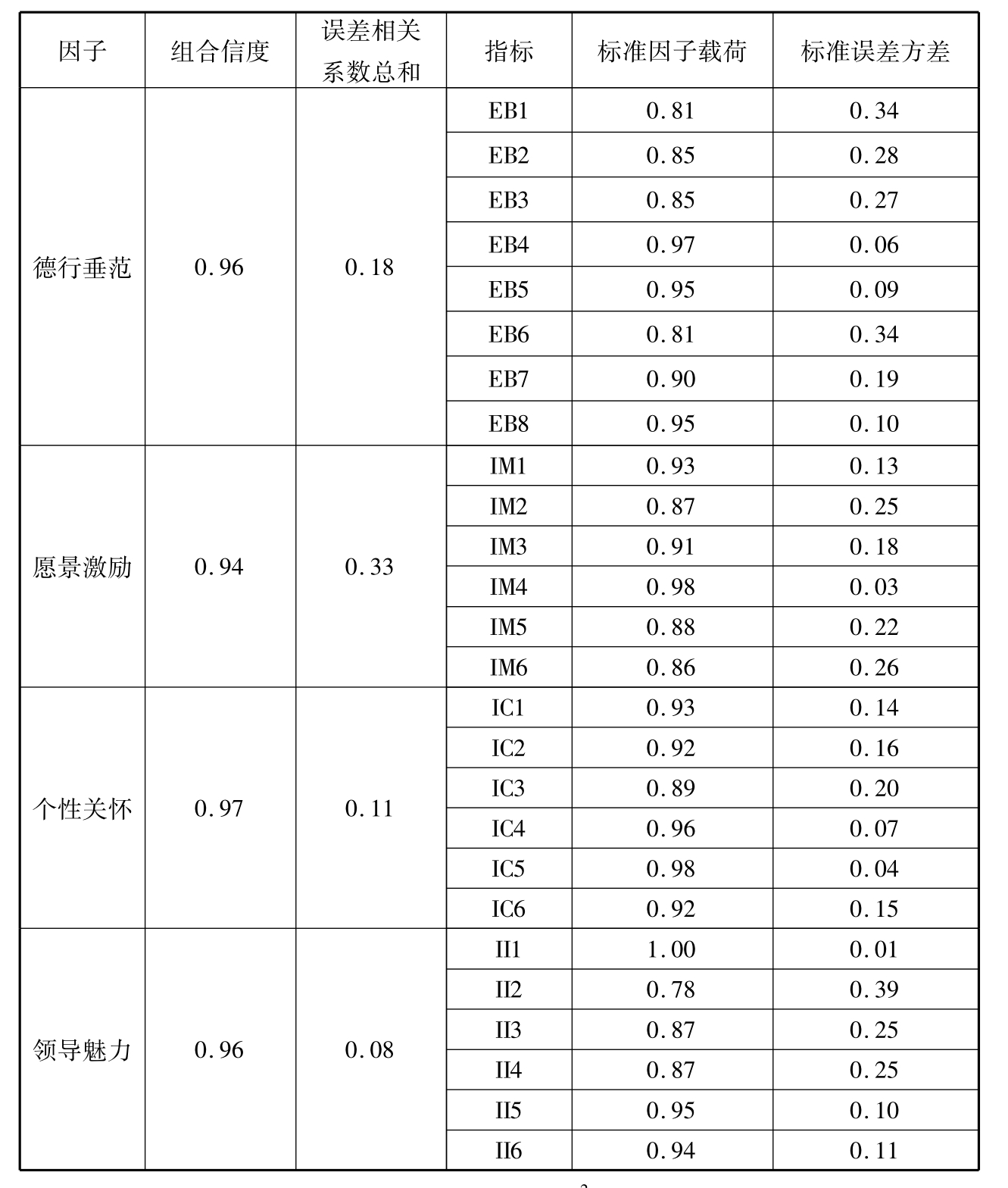
在结构方程模型中，信度估计延续了古典测量理论的观点，将信度视为真实分数所占的比例，而测量误差的变异即为观察分数当中无法反映真实分数的残差变异量。Fornell＆Larcker(1981)提出可以通过组合信度来检验潜在变量的信度。根据古典测量理论的观点，量表信度达到0.7时才属于比较稳定的测量，在结构方程模型中同样沿用这一标准。在本研究中，采用变革型领导的二阶测量模型作为最终模型，因此我们主要检验变革型领导二阶测量模型的信度。潜变量德行垂范、愿景激励、个性化关怀与领导魅力的组合信度分别为0.96、0.94、0.96与0.97，均达到要求，可见测量信度是比较理想的。信度检验的具体结果如表4-13所示。

4.4.1.3　收敛效度检验

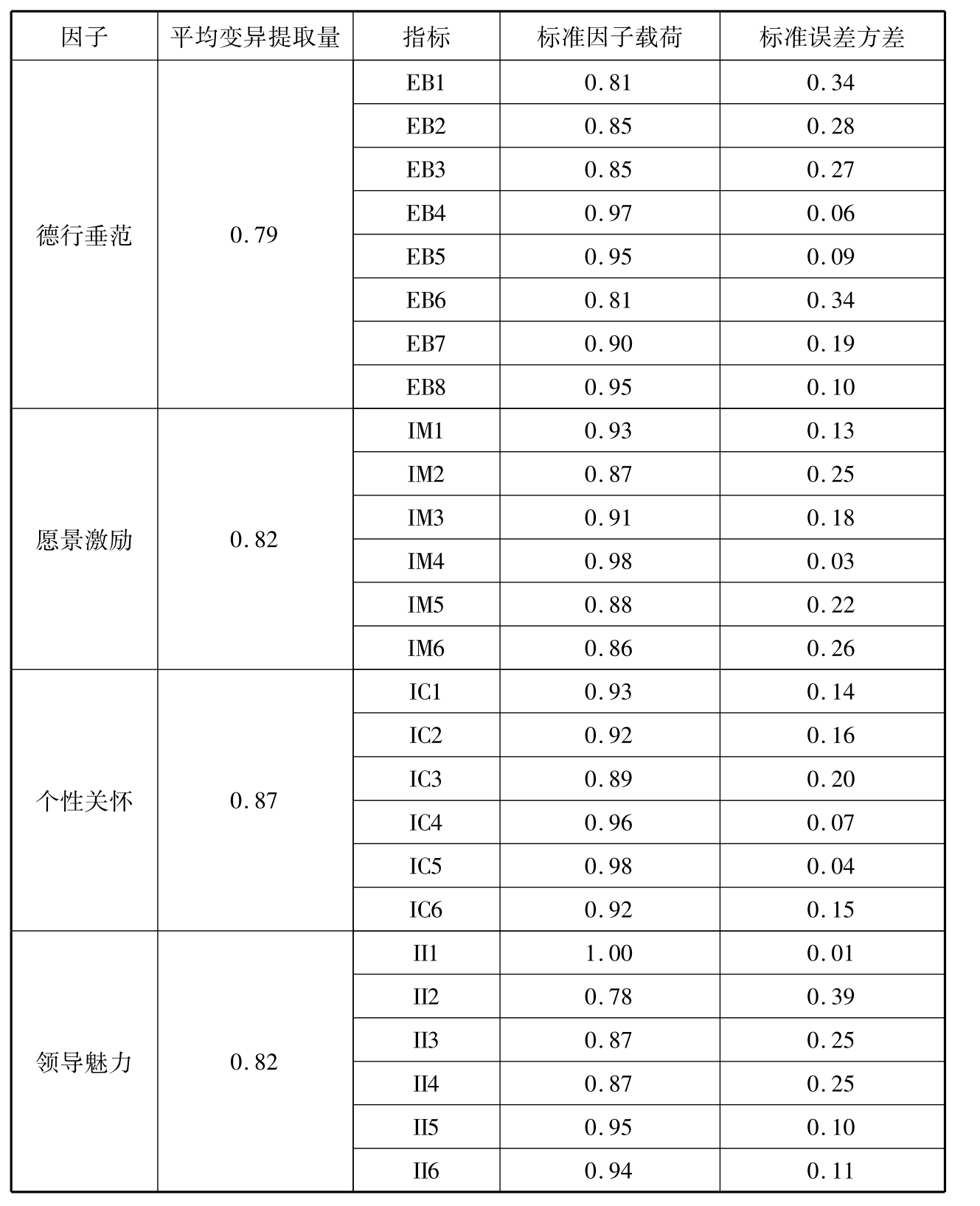
收敛效度用来检验观察变量是否能很好地反映潜变量。指标的收敛效度越好，则表明指标越能反映潜变量，因子能够解释各观察变量的变异程度越大，进而说明该指标隶属于该因子;相反，如果指标的收敛效度不能达到要求，则说明该指标不能反映潜变量，进而指标不属于该因子。一般通过两个方面对指标的收敛效度进行检验。Hair认为当因子载荷大于0.5时，指标具有良好的收敛效度。Fornell＆Larcker则从平均变异萃取量(AVE)来判断潜在变量的收敛效度。当平均变异萃取量大于0.5时，表示潜在变量的收敛效度十分理想(邱皓政、林碧芳，2009)。在本研究中，变革型领导的二阶测量模型的各指标因子载荷均大于0.5，平均变异的萃取量均大于0.5，说明本研究所选变革型领导的二阶测量模型具有良好的收敛效度。收敛效度检验的具体结果如表4-14所示。

表4-13　变革型领导测量信度检验

注:组合信度测量公式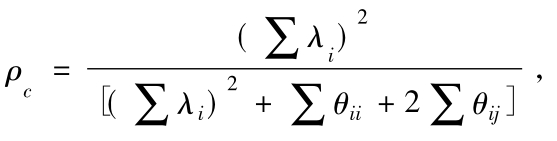其中(∑λ_i)²表示因子载荷加总后取平方数值;∑θ_ii表示误差方差总和;∑θ_ij表示误差方差相关系数总和。

表4-14　变革型领导收敛效度检验

注:平均变异萃取量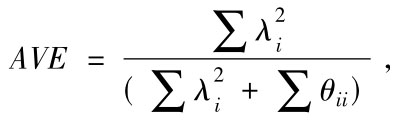其中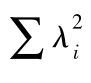表示因子载荷平方和;∑θ_ii表示误差方差。

4.4.2　团队学习

团队学习是本研究中另一个重要的变量，根据已有的相关理论以及前面探索性因子分析的结果，团队学习包含了发现、反馈、沟通和创新4个因子及11个指标。同样运用LISREL8.80软件对团队学习进行一阶验证性因子分析与二阶验证性因子分析，所输出的团队学习二阶与一阶验证性因子分析结果分别如图4-3、图4-4所示。

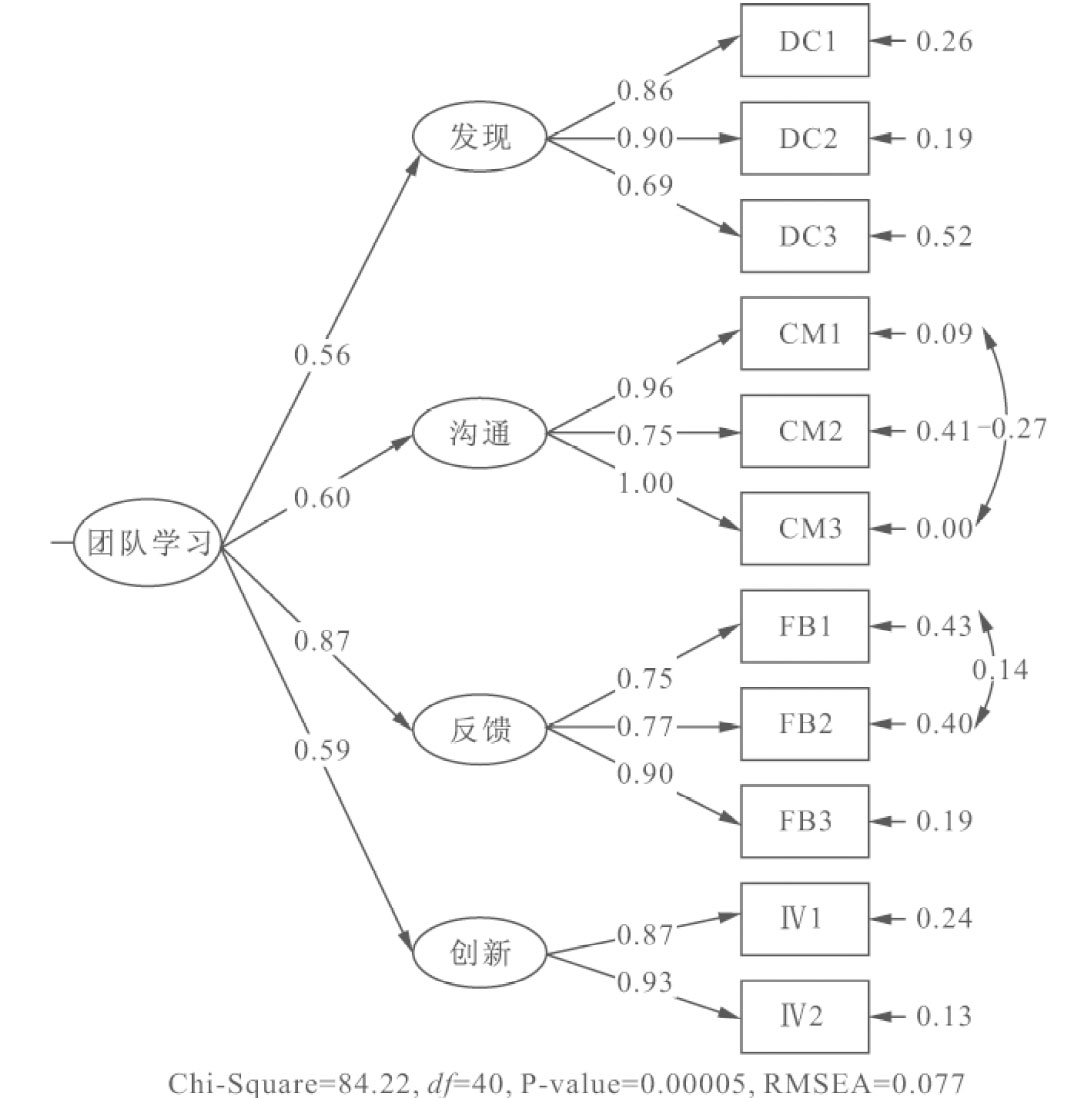
图4-3　团队学习二阶验证性因子分析

4.4.2.1　模型拟合评价(www.xing528.com)

同样，在选择团队学习的最终测量模型时，首先需要对经过验证性因子分析的模型进行评价，然后比较各模型的拟合情况。对模型的拟合同样采用卡方与自由度的比值(χ²/df)、标准化残差均方根指数(SRMR)、赋范模拟指数(NFI)、非范模拟指数(NNFI)、比较拟合指数(CFI)、拟合优度(GFI)与近似误差均方根(RMSEA)作为模型拟合评价指数。根据团队学习二阶和一阶验证性因子分析的结果分析报告，二阶和一阶测量模型的拟合指标值如表4-15所示。

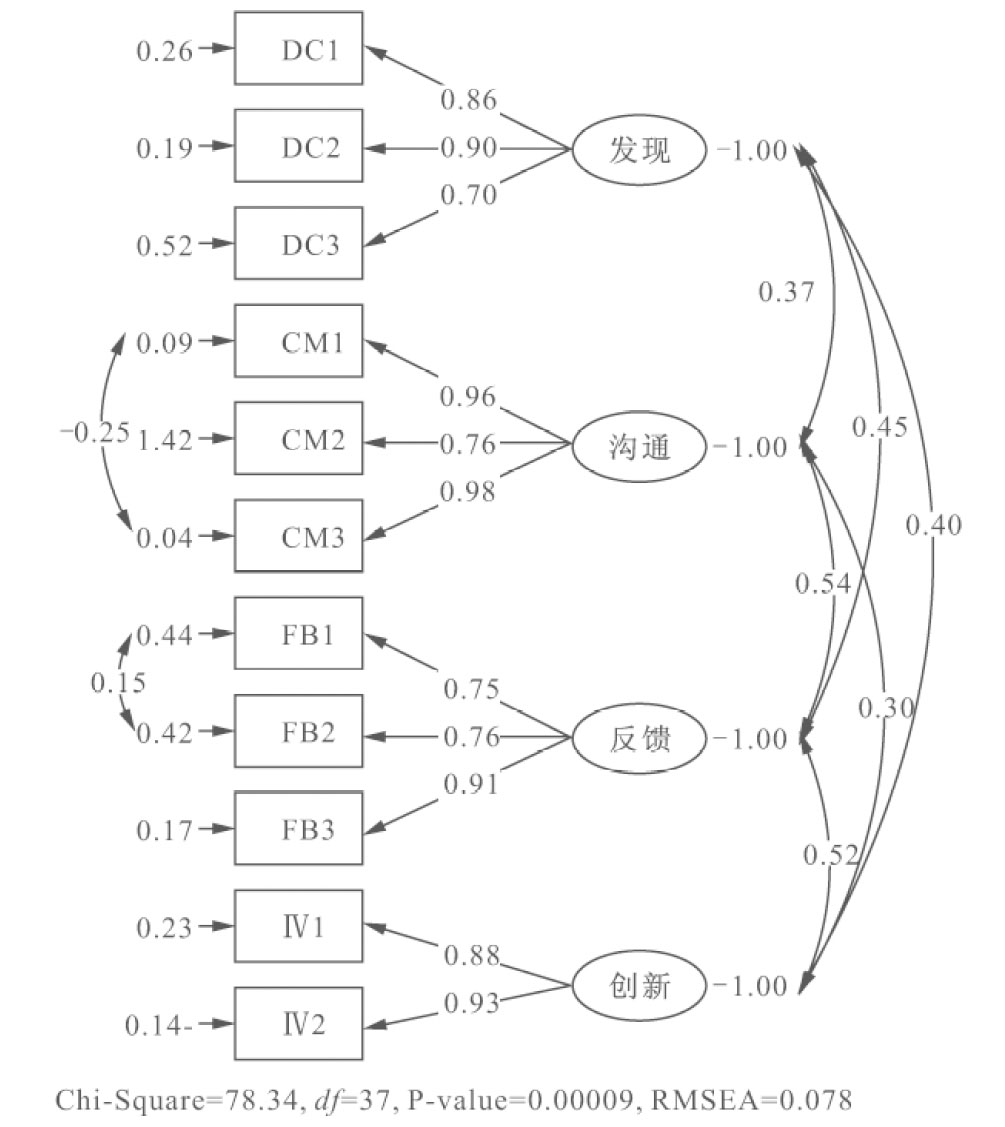
图4-4　团队学习一阶验证性因子分析

由表4-15可以看出，团队学习的二阶测量模型与一阶测量模型的拟合情况均达到标准，拟合情况良好。将两个测量模型的拟合情况进行比较，二阶测量模型的拟合情况要优于一阶测量模型。从理论上分析，团队学习包含了发现、沟通、反馈与创新四个维度，也就是说发现、沟通、反馈与创新4个初阶因子受到一个共同的高阶因子团队学习所决定。从理论分析和模型的实证检验来看，二阶模型都要优于一阶模型。因此本研究采用团队学习的二阶测量模型作为最终的模型。

表4-15　团队学习二阶和一阶测量模型拟合评价指数

4.4.2.2　信度检验

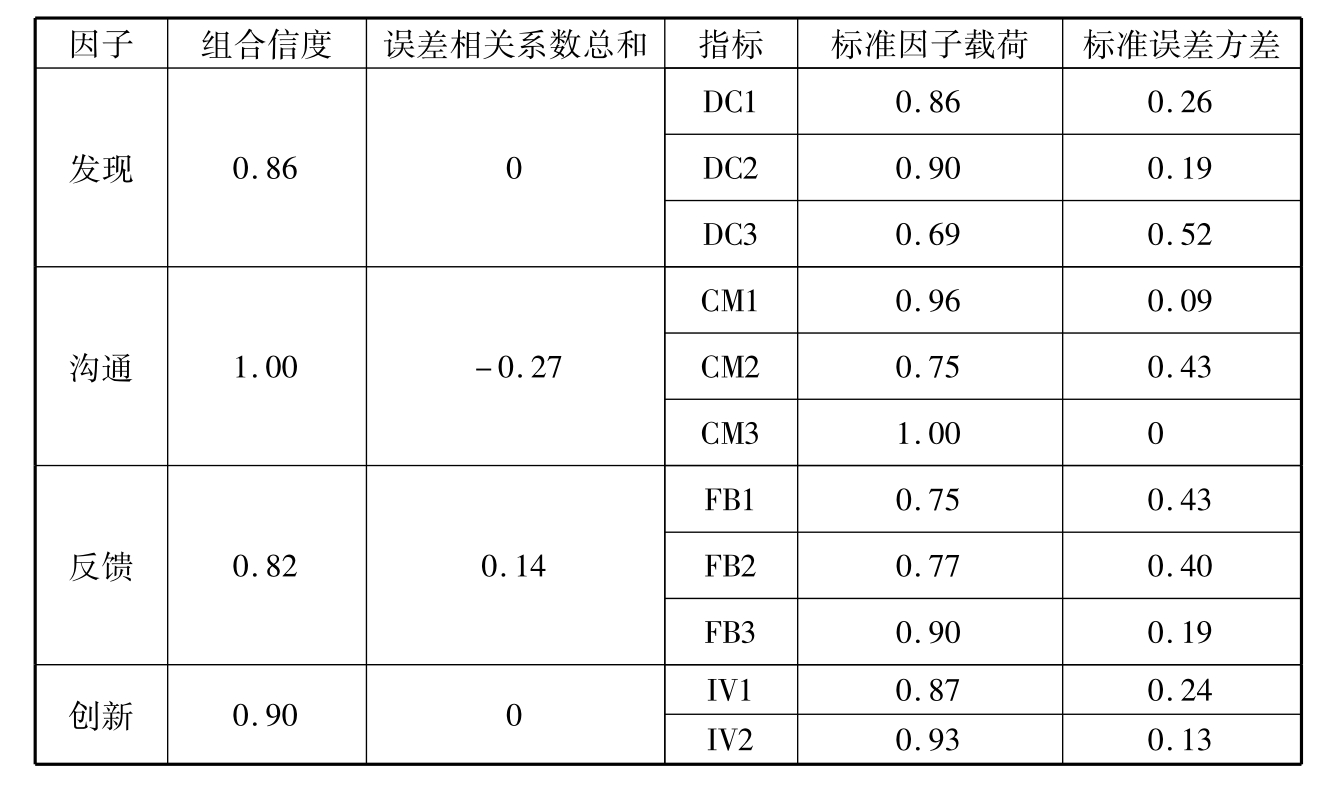
根据团队学习的相关理论，结合团队学习测量模型的实证检验，本研究选择团队学习的二阶测量模型作为最终模型。同样采用组合信度对团队学习的二阶模型进行信度检验，模型中的潜变量发现、沟通、反馈与创新的组合信度分别为0.86、1.00、0.82与0.90，均达到要求，因此测量信度是比较理想的。团队学习信度检验的具体结果如表4-16所示。

表4-16　团队学习测量信度检验

4.4.2.3　收敛效度检验

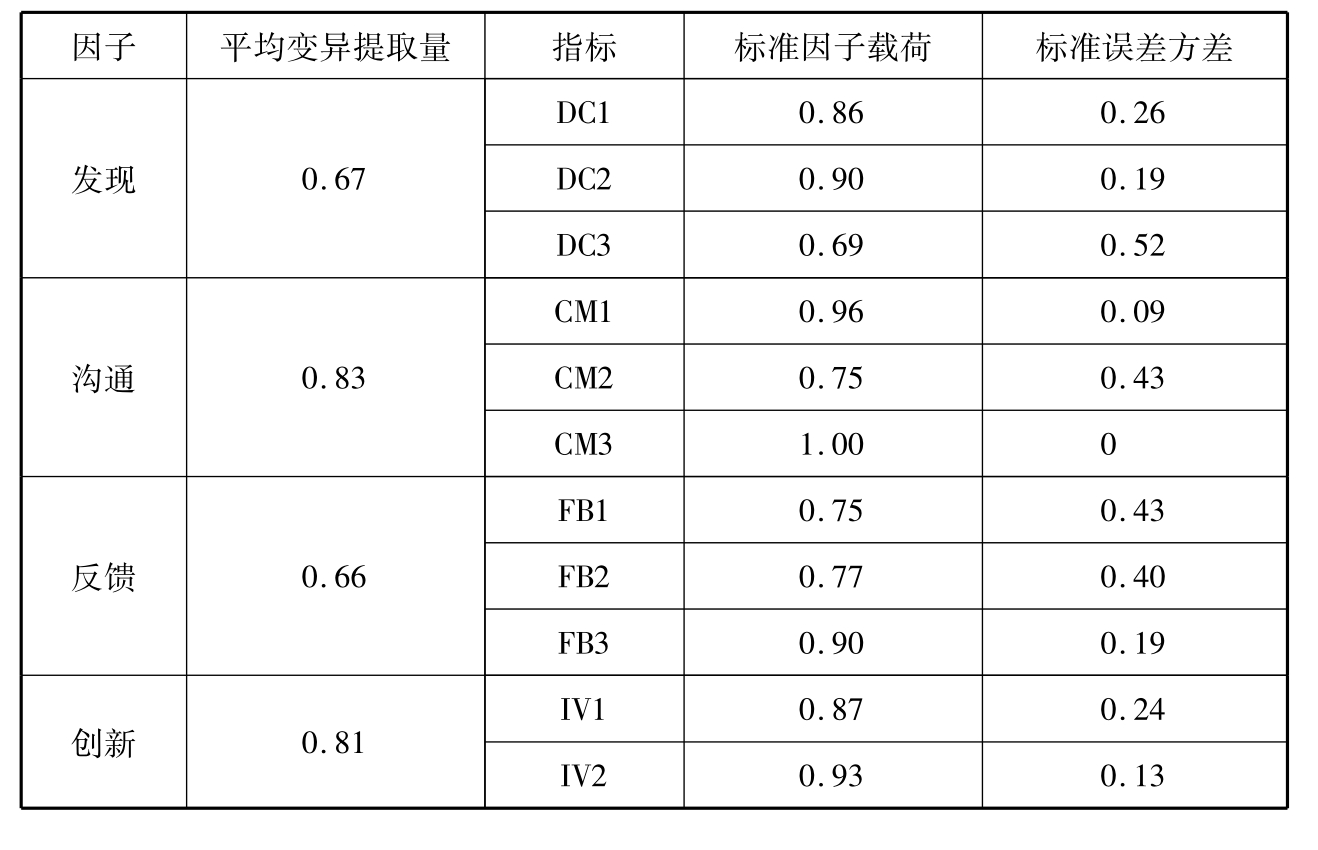
同变革型领导的测量模型一样，仍然需要对所选团队学习的二阶测量模型的收敛效度进行检验，用来检验团队学习的观察变量是否能很好地反映发现、沟通、反馈和创新等潜变量。在进行收敛效度检验的过程中，同样根据模型中各指标的因子载荷以及潜在变量的平均变异萃取量来进行判断。本研究中，潜变量发现、沟通、反馈与创新的平均变异萃取量分别为0.67、0.83、0.66与0.81，各指标的因子载荷均大于0.5，具体结果如表4-17所示。说明团队学习的二阶测量模型具有很好的收敛效度。

表4-17　团队学习收敛效度检验

4.4.3　团队绩效

团队绩效是本研究中的另外一个主要变量，同变革型领导与团队学习一样，根据探索性因子分析的结果，团队绩效包含了任务绩效、满意度与发展能力三个因子以及10个指标。同样运用LISREL8.80软件对团队绩效进行一阶验证性因子分析与二阶验证性因子分析，所输出的团队绩效二阶与一阶验证性因子分析结果如图4-5、图4-6所示。

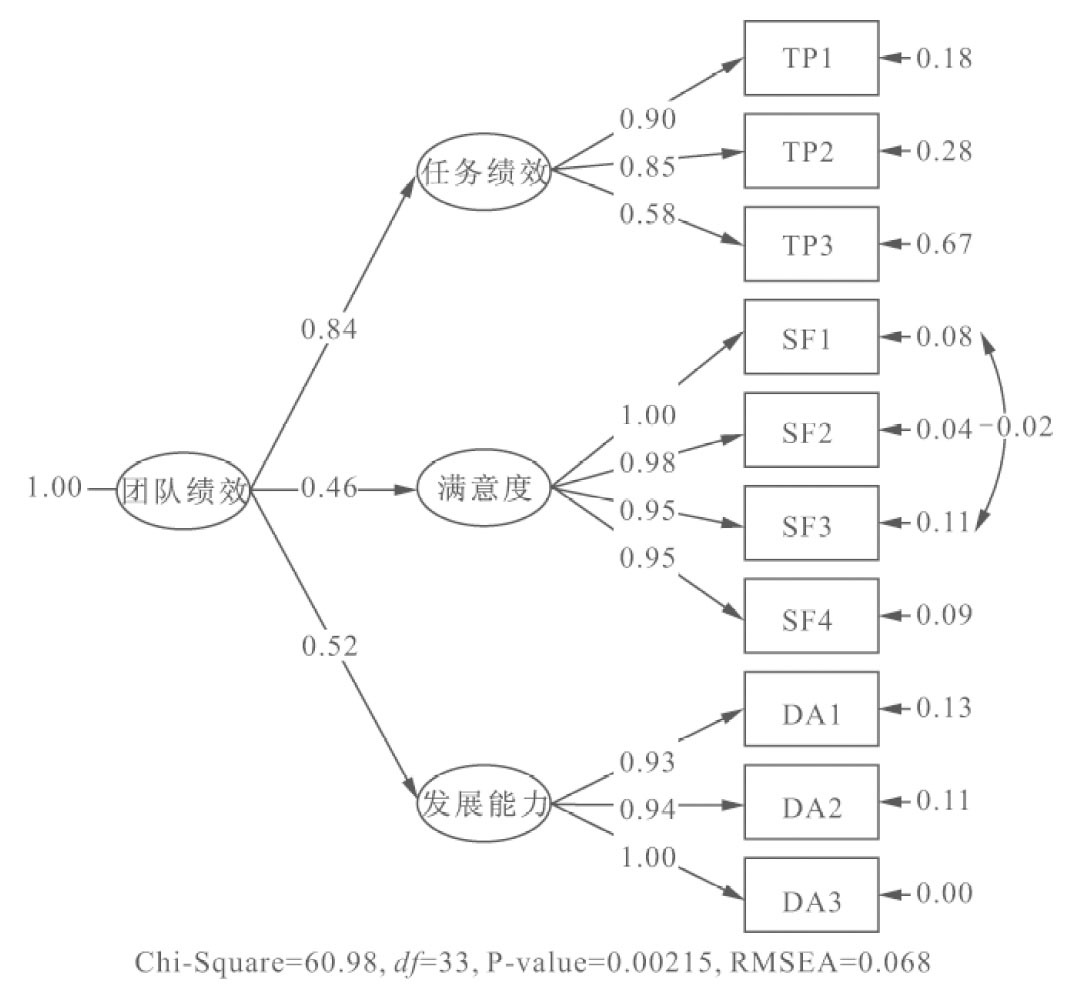
图4-5　团队绩效二阶验证性因子分析

4.4.3.1　模型拟合评价

同变革型领导与团队学习一样，需要对团队绩效的验证性因子分析模型进行评价，然后比较各模型的拟合情况。对模型的拟合采用与变革型领导和团队学习测量模型相同的评价指数(χ²/df、SRMR、NFI、NNFI、CFI、GFI与RMSEA)。根据团队绩效二阶和一阶验证性因子分析的结果分析报告，二阶和一阶测量模型的拟合指标值如表4-18所示。

从表4-18中可以看出，团队绩效的二阶测量模型与一阶测量模型的拟合情况均达到标准，拟合情况良好。将两个测量模型的拟合情况进行比较，二阶测量模型的拟合情况总体要优于一阶测量模型。从理论上分析，团队绩效包含了任务绩效、满意度与发展能力三个维度，也就是说，任务绩效、满意度与发展能力3个初阶因子受到一个共同的高阶因子团队绩效所决定。从理论分析和模型的实证检验来看，二阶模型都要优于一阶模型。因此本研究也选用团队绩效的二阶测量模型作为最终模型。

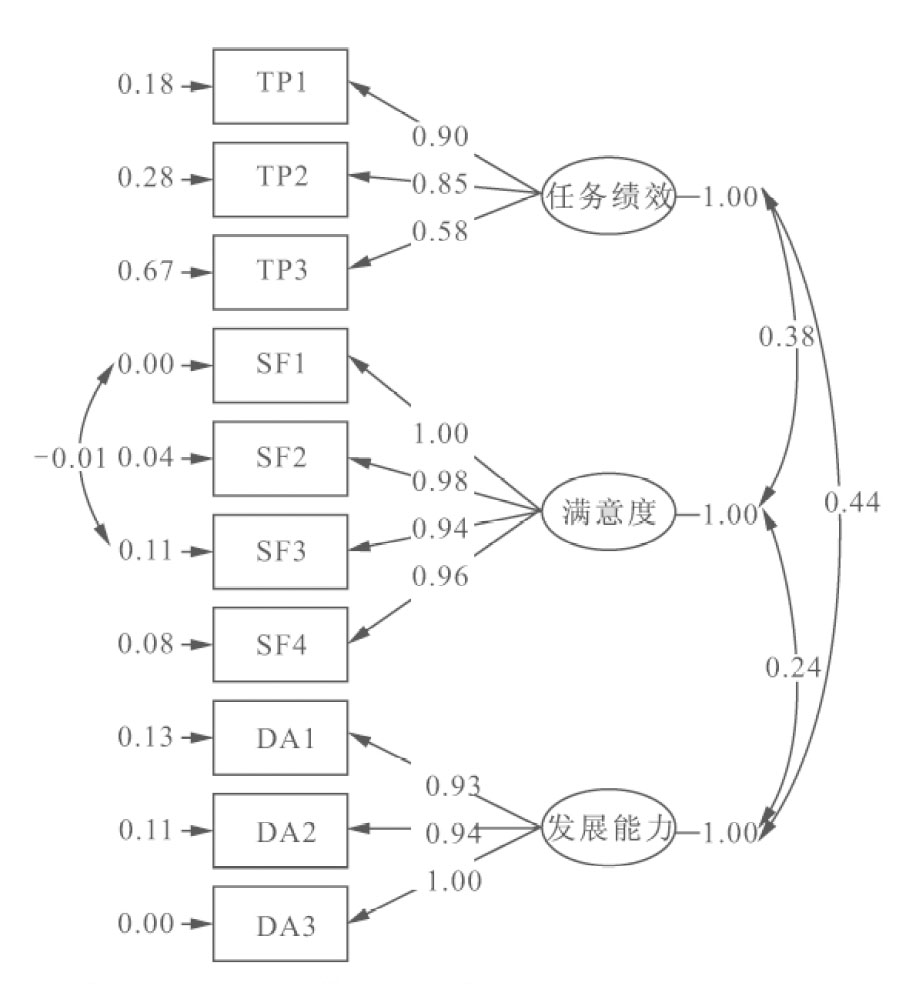
图4-6　团队绩效一阶验证性因子分析

表4-18　团队绩效二阶和一阶测量模型拟合评价指数

4.4.3.2　信度检验

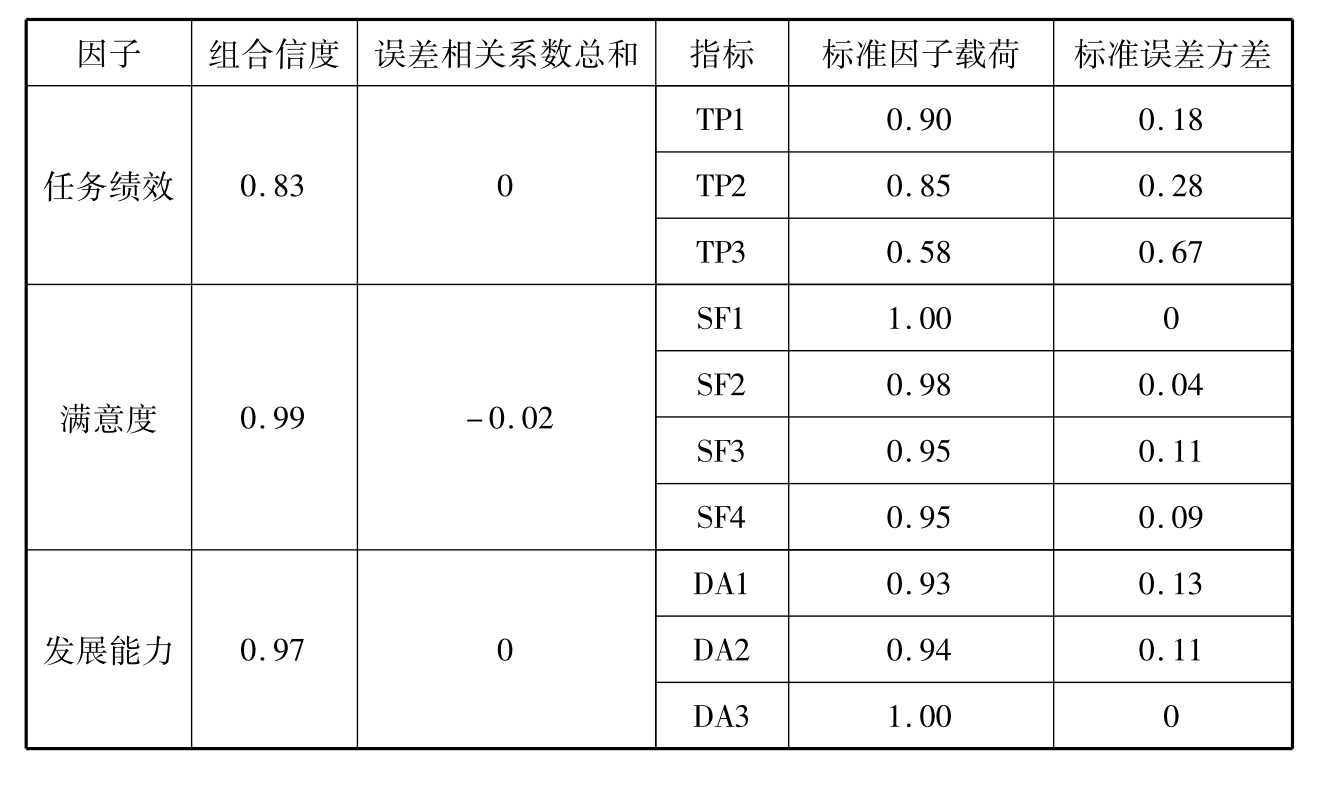
本研究选择团队绩效的二阶测量模型为最终模型，同样采用组合信度对团队绩效的二阶模型进行信度检验。模型中的潜变量任务绩效、满意度与发展能力的组合信度分别为0.83、0.99与0.97，均达到统计学要求，模型具有较好的测量信度。团队绩效信度检验的具体结果如表4-19所示。

表4-19　团队绩效测量信度检验

4.4.3.3　收敛效度检验

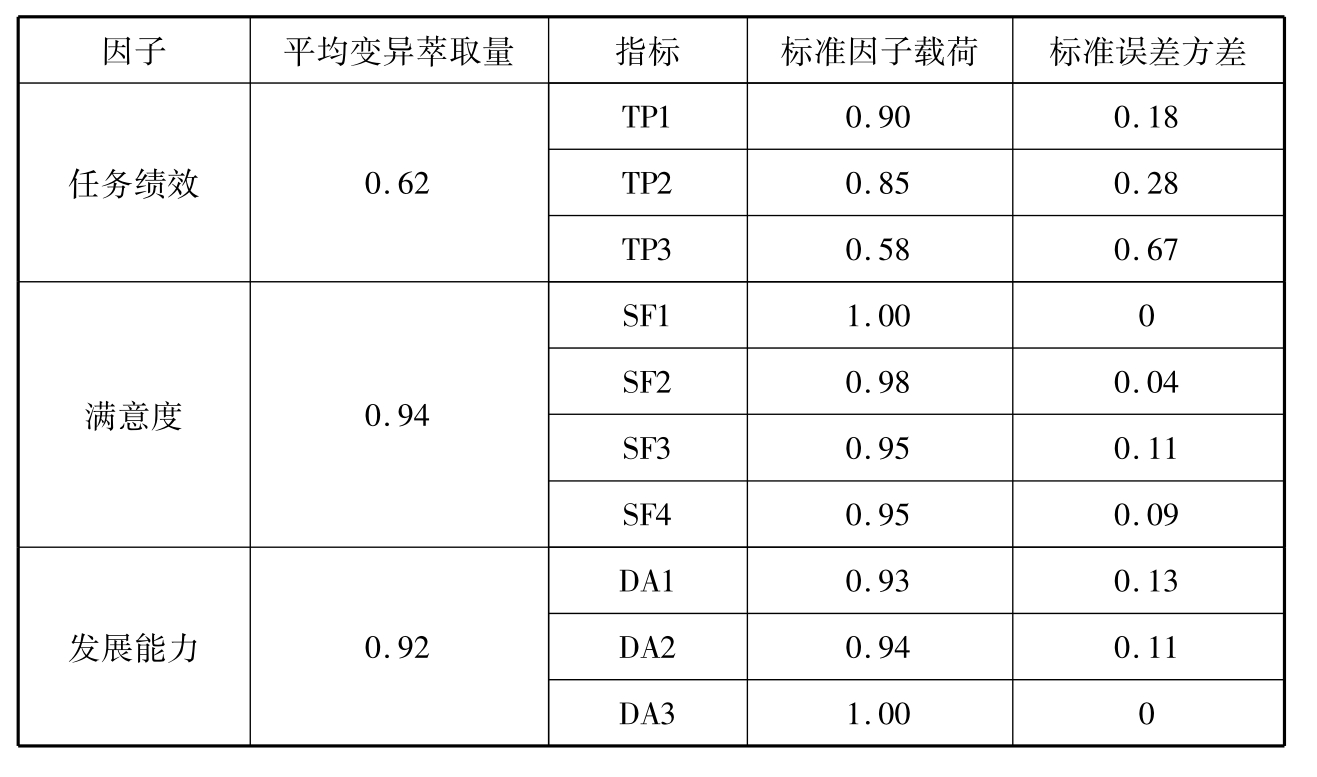
同变革型领导和团队学习一样，仍需要对所选团队绩效二阶测量模型的收敛效度进行检验，用来说明团队绩效的观察变量是否能很好地反映任务绩效、满意度和发展能力等潜变量。在进行收敛效度检验的过程中，同样根据模型中各指标的因子载荷以及潜在变量的平均变异萃取量来进行判断。本研究中，潜变量任务绩效、满意度与发展能力的平均变异萃取量分别为0.62、0.94与0.92，各指标的因子载荷均大于0.5，具体结果如表4-20所示。说明所选团队绩效的二阶测量模型具有很好的收敛效度。

表4-20　团队绩效收敛效度检验