二、土方调配
土方调配是大型土方施工设计的一个重要内容。土方调配的目的是在使土方总运输量(m3·m)最小或土方运输成本(元)最小的条件下,确定填挖方区土方的调配方向和数量,从而达到缩短工期和降低成本的目的。
(一)土方调配区的划分、平均运距和土方施工单价的确定
1.调配区的划分原则
进行土方调配时,首先要划分调配区。划分调配区应注意下列几点:
(1)调配区的划分应该与工程建(构)筑物的平面位置相协调,并考虑它们的开工顺序、工程的分期施工顺序;
(2)调配区的大小应该满足土方施工主导机械(铲运机、挖土机等)的技术要求;
(3)调配区的范围应该和土方工程量计算用的方格网协调,通常可由若干个方格组成一个调配区;
(4)当土方运距较大或场地范围内土方不平衡时,可根据附近地形,考虑就近取土或就近弃土,这时一个取土区或弃土区都可作为一个独立的调配区。
2.平均运距的确定
调配区的大小和位置确定之后,便可计算各填、挖方调配区之间的平均运距。当用铲运机或推土机平土时,挖土方调配区和填方调配区土方重心之间的距离,通常就是该填、挖方调配区之间的平均运距。
当填、挖方调配区之间距离较远,采用汽车、自行式铲运机或其他运土工具沿工地道路或规定线路运土时,其运距应按实际情况进行计算。
3.土方施工单价的确定
如果采用汽车或其他专用运土工具运土时,调配区之间的运土单价,可根据预算定额确定。
当采用多种机械施工时,确定土方的施工单价就比较复杂,因为不仅是单机核算问题,还要考虑运、填配套机械的施工单价,确定一个综合单价。
将上述平均运距或土方施工单价的计算结果填入土方平衡与施工运距(单价)表(表1-4)内。
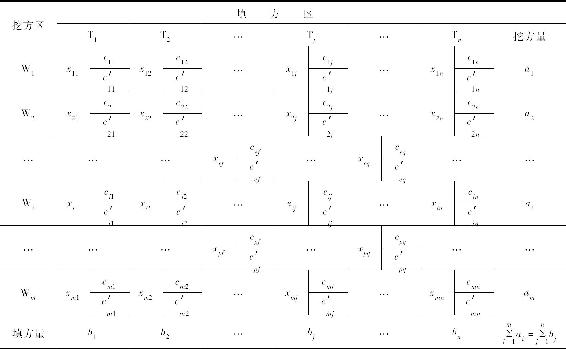
表1-4 土方平衡与施工运距(单价)
(二)用“线性规划”方法进行土方调配时的数学模型
表1-4是土方平衡与施工运距(单价)表。
上列表格说明了整个场地划分为m个挖方区W1,W2,…,Wm,其挖方量相应为a1,a2,…,am;有n个填方区T1,T2,…,Tn,其填方量相应为b1,b2,…,bn;xij表示由挖方区i到填方区j的土方调配数,由填挖方平衡,即

从W1到T1的价格系数(平均运距,或单位土方运价,或单位土方施工费用)为c11,一般地,从Wi到Tj的价格系数为cij。于是土方调配问题可以用下列数学模型表达:求一组xij的值,使目标函数

为最小值,并满足下列约束条件:
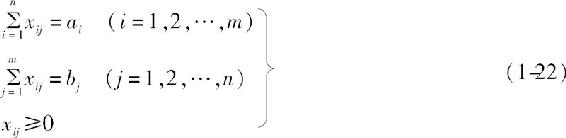
根据约束条件知道,未知量有m×n个,而方程数为m+n个。由于填挖平衡,前面m个方程相加减去后面n-1个方程之和可以得到第n个方程,因此,独立方程的数量实际上只有m+n-1个。
由于未知量个数多于独立方程数,因此,方程组有无穷多的解,而我们的目的是求出一组最优解,使目标函数为最小。这属于“线性规划”中的“运输问题”,可以用“单纯形法”或“表上作业法”求解。运输问题用“表上作业法”求解较方便,用“单纯形法”则较繁琐。
下面介绍“表上作业法”进行土方调配的方法,这个方法是通过“假想价格系数”求检验数的。
表1-4中 表示假想系数,其值待定。
表示假想系数,其值待定。
(三)用“表上作业法”进行土方调配
下面结合一个例子,说明用表上作业法求调配最优解的步骤与方法。
图1-9为一矩形广场,图中小方格的数字为各调配区的土方量,箭杆上的数字则为各调配区之间的平均运距。试求土方调配最优方案。

图1-9 各调配区的土方量和平均运距
1.编制初始调配方案
初始方案的编制采用“最小元素法”,即对应于价格系数cij最小的土方量xij取最大值,由此逐个确定调配方格的土方数及不进行调配的方格,并满足式(1-22)。
首先将图1-9中的土方数及价格系数(本例即平均运距)填入计算表格中(表1-5)。
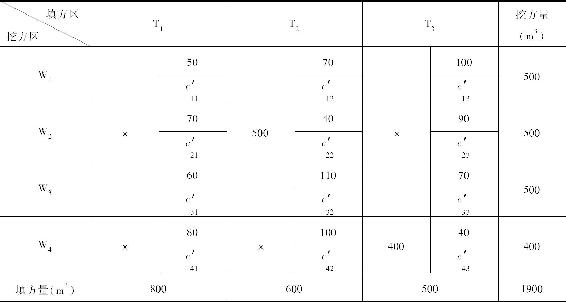
表1-5 各调配区土方量及平均运距

在表1-5中找价格系数最小的方格,确定它所对应的调配土方数。本例最小的为c22及c43,(c22=c43=40),任取其中之一,如取c43,则先确定x43的值,使x43尽可能大,考虑挖方区W4最大挖方量为400,填方区T3最大填方量为500,则x43最大为400。由于W4挖方区的土方全部调到T3填方区,所以x41和x42都等于零。将400填入表1-6中的x43格内,同时在x41,x42格内画上一个“×”号。然后在没有填上数字和“×”号的方格内,再选一个cij最小的方格,即c22=40,我们使x22尽量大,x22=min(500,600)=500,同时使x21=x23=0。将500填入表1-6的x22格内,并在x21,x23格内画上“×”号(表1-6)。
表1-6 初始方案确定过程
重复上面步骤,依次地确定其余xij数值,最后可以得出表1-7。(https://www.xing528.com)
表1-7 初始方案计算结果
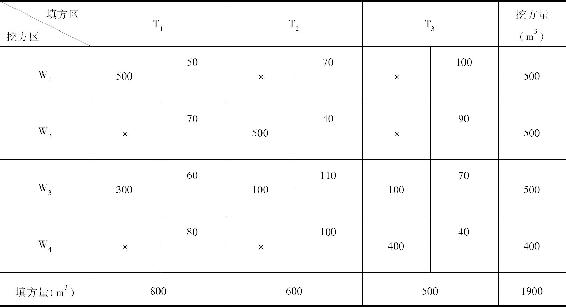
表1-7中所求得的一组xij的数值,便是本例的初始调配方案。由于利用“最小元素法”确定的初始方案首先是让cij最小的那些格内的xij值取尽可能大的值,也就是考虑“最优调配”,所以求得之总运输量(或总费用)是较小的。但是这并不能保证其总运输量(或总费用)是最小,因此,还需要进行判别,看它是否是最优方案。
2.最优方案判别法
在“表上作业法”中,判别是否最优方案的方法有许多。采用“假想价格系数法”求检验数较清晰直观,此处介绍该方法。该方法是求得无调配土方的方格(如本例中的W1-T3,W4-T2等方格)的检验数λij,并判别λij是否非负,如所有检验数λij≥0,则方案为最优方案,否则该方案不是最优方案,需要进行调整。
首先求出表中各个方格的假想价格系数 ,有调配土方方格的假想价格系数
,有调配土方方格的假想价格系数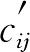 =cij,无调配土方方格的假想系数用下式计算:
=cij,无调配土方方格的假想系数用下式计算:

式(1-23)的意义即构成任一矩形的四个方格内对角线上的假想价格系数之和相等(参见表1-4)。
利用已知的假想价格系数,逐个求解未知的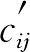 。寻找适当的方格构成一个矩形,最终能求得所有的cij。这些计算,均在表上作业。
。寻找适当的方格构成一个矩形,最终能求得所有的cij。这些计算,均在表上作业。
在表1-7的基础上先将有调配土方的方格的假想价格系数填入方格的右下角。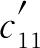 =50,
=50,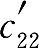 =40,
=40,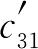 =60,
=60,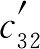 =110,
=110,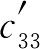 =70,
=70,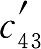 =40,寻找适当的方格由式(1-23)即可计算得全部假想价格系数。例如,由
=40,寻找适当的方格由式(1-23)即可计算得全部假想价格系数。例如,由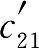 +
+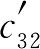 =
= +
+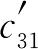 可得
可得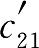 =-10(表1-8)。
=-10(表1-8)。
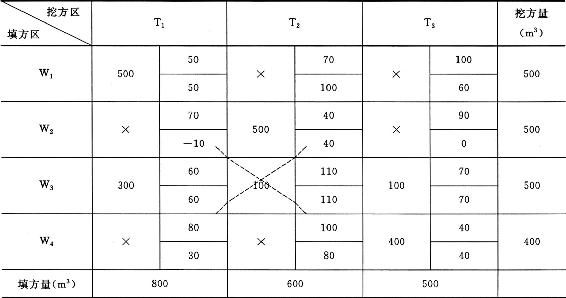
表1-8 计算假想价格系数
假想价格系数求出后,按下式求出表中无调配土方方格的检验数:

只要把表中无调配土方的方格右边两小格的数字上下相减即可。如λ21=70-(-10)=+80,λ12=70-100=-30。将计算结果填入表1-9。表1-9中只写出各检验数的正负号,因为我们只对检验数的符号感兴趣,而检验数的值对求解结果无关,因而可不必填入具体的值。
表1-9 计算检验数
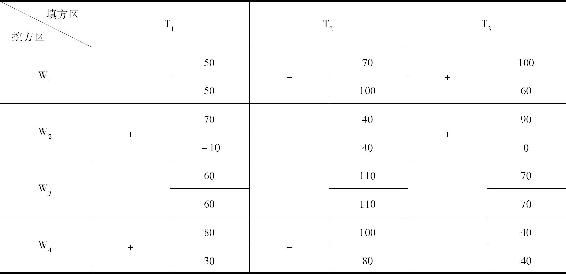
表1-9中出现了负检验数,说明初始方案不是最优方案,需要进一步进行调整。
3.方案的调整
第一步 在所有负检验数中选一个(一般可选最小的一个),本例中便是λ12,把它所对应的变量x12作为调整对象。
第二步 找出x12的闭回路。其做法是:从x12格出发,沿水平与竖直方向前进,遇到适当的有数字的方格作90°转弯(也不一定转弯),然后继续前进,如果路线恰当,经有限步骤便能回到出发点,形成一条以有数字的方格为转角点的、用水平和竖直线联起来的闭合回路(表1-10)。
表1-10 求解闭合回路

第三步 从空格x12出发,沿着闭回路(方向任意)一直前进,在各奇数次转角点(以x12出发点为0)的数字中,挑出一个最小的(本例中便是在x11(500)及x32(100)中选出“100”),将它由x32调到x122方格中(即空格中)。
第四步 将“100”填入x12方格中,被调出的x32为0(该格变为空格);同时将闭回路上其他的奇数次转角上的数字都减去“100”,偶数次转角上数字都增加“100”,使得填挖方区的土方量仍然保持平衡,这样调整后,便可得到表1-11的新调配方案。
表1-11 调整后的新调配方案
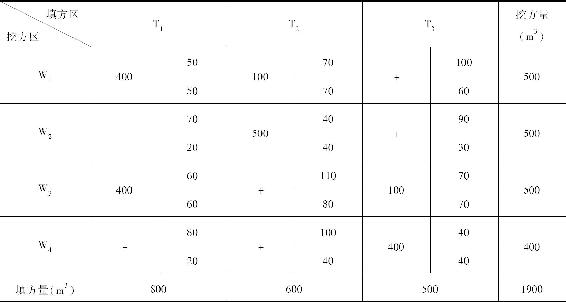
对新调配方案,再进行检验,看其是否已是最优方案。如果检验数中仍有负数出现,那就仍按上述步骤继续调整,直到找出最优方案为止。
表1-11中所有检验数均为正号,故该方案即为最优方案。
该最优土方调配方案的土方总运输量为
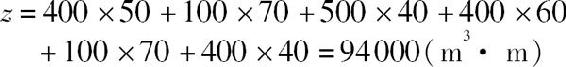
将表1-11中土方调配数值绘成土方调配图(图1-10)。图中箭杆上数字为土方调配数。
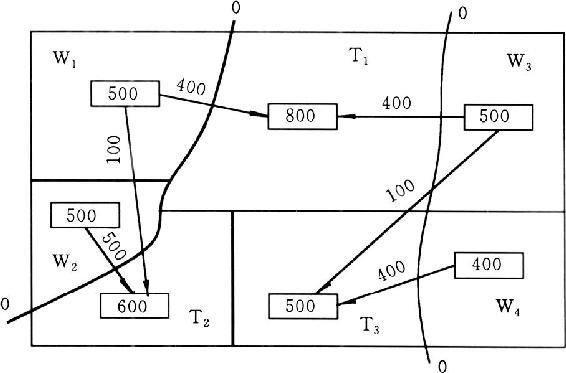
图1-10 土方调配图
最后,我们来比较一下最佳方案与初始方案的运输量:
初始方案的土方总运输量为
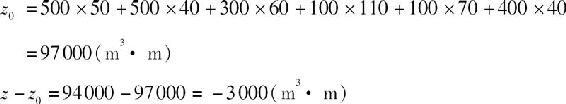
即调整后总运输量减少了3000(m3·m)。
土方调配的最优方案可以不只是一个,这些方案调配区或调配土方量可以不同,但它们的目标函数z都是相同的。有若干最优方案,为人们提供了更多的选择余地。
当土方调配区数量较多时,用上述表上作业法计算最优方案仍较费工。如采用手工计算,要找出所有最优方案需经过多次轮番计算,工作量很大。现已有较完善的电算程序,能准确、迅速地求得最优方案,而且还能得到所有可能的最优方案。图1-11是土方调配最优方案计算的电算程序框图。
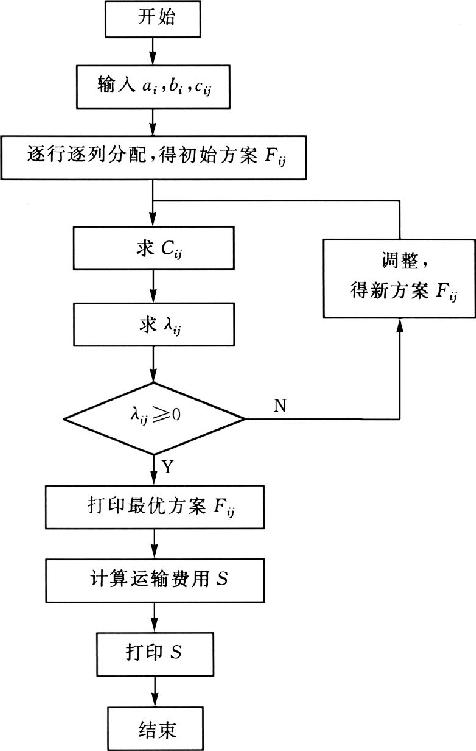
图1-11 土方调配程序框图
“线性规划”求最优解的方法,不仅可在土方调配中应用,而且可在钢筋下料、运输调度及土方机械选择等优化设计中应用。关于线性规划的理论及计算方法详见有关专著。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




