最佳设计平面：最小二乘法解析

二、用最小二乘法原理求最佳设计平面

按上述方法得到的设计平面，能使挖方量与填方量平衡，但不能保证总的土方量最小。应用最小二乘法的原理，可求得满足上述两个条件的最佳设计平面。

当地形比较复杂时，一般需设计成多平面场地，此时可根据工艺要求和地形特点，预先把场地划分成几个平面，分别计算出最佳设计单平面的各个参数，然后适当修正各设计单平面交界处的标高，使场地各单平面之间的变化缓和且连续。因此，确定单平面的最佳设计平面是竖向规划设计的基础。

我们知道，任何一个平面在直角坐标体系中都可以用三个参数c，i_x，i_y来确定（图1-3）。在这个平面上任何一点i的标高z′_i，可以根据下式求出：

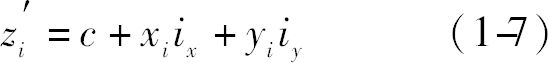
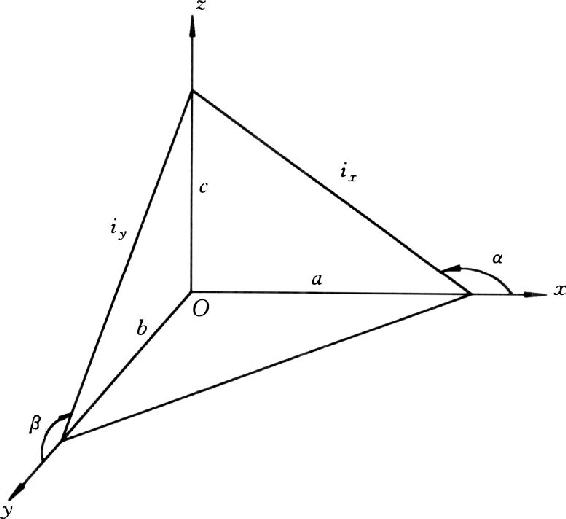
图1-3　一个平面的空间位置

c—原点标高；i_x＝tanα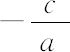＝，x方向的坡度；

i_y＝tanβ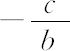＝，y方向的坡度

式中　x_i——i点在x方向的坐标；

y_i——i点在y方向的坐标。

与前述方法类似，将场地划分成方格网，并将原地形标高z_i标于图上，设最佳设计平面的方程式为式（1-7），则该场地方格网角点的施工高度为

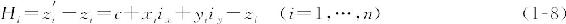
式中　H_i——方格网各角点的施工高度；

z′_i——方格网各角点的设计平面标高；

z_i——方格网各角点的原地形标高；

n——方格角点总数。

由土方量计算公式（式（1-14）～式（1-19））可知，施工高度之和与土方工程量成正比。由于施工高度有正有负，当施工高度之和为零时，则表明该场地土方的填挖平衡，但它不能反映出填方和挖方的绝对值之和为多少。为了不使施工高度正负相互抵消，若把施工高度平方之后再相加，则其总和能反映土方工程填挖方绝对值之和的大小。但要注意，在计算施工高度总和时，应考虑方格网各点施工高度在计算土方量时被应用的次数p_i，令σ为土方施工高度之平方和，则

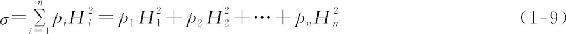(www.xing528.com)

将式（1-8）代入式（1-9），得

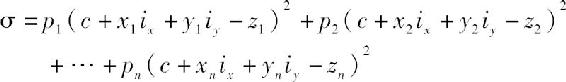
当σ的值最小时，该设计平面既能使土方工程量最小，又能保证填挖方量相等（填挖方不平衡时，上式所得数值不可能最小）。这就是用最小二乘法求设计平面的方法。

为了求得σ最小时的设计平面参数c，i_x，i_y，可以对上式的c，i_x，i_y分别求偏导数，并令其为0，于是得

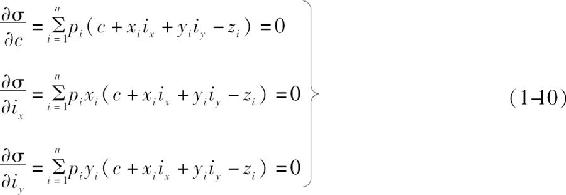
经过整理，可得下列准则方程：

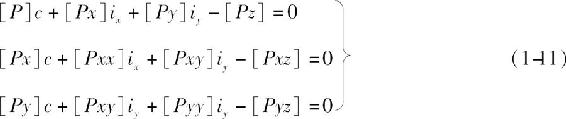
式中　［P］＝P₁＋P₂＋…＋P_n

［Px］＝P₁x₁＋P₂x₂＋…＋P_nx_n

［Pxx］＝P₁x₁x₁＋P₂x₂x₂＋…＋P_nx_nx_n

［Pxy］＝P₁x₁y₁＋P₂x₂y₂＋…＋P_nx_ny_n

其余类推。

解联立方程组（1-11），可求得最佳设计平面（此时尚未考虑工艺、运输等要求）的三个参数c，i_x，i_y。然后即可根据方程式（1-3）算出各角点的施工高度。

应用上述准则方程时，若已知c或i_x，或i_y时，只要把这些已知值作为常数代入，即可求得该条件下的最佳设计平面，但它与无任何限制条件下求得的最佳设计平面相比，其总土方量一般要比后者大。

例如，要求场地为水平面（即i_x＝i_y＝0），则由式（1-11）中的第一式可得

c就是场地为水平面时的设计标高，它与式（1-4）中的z₀的意义完全相同，说明按式（1-14）方法所得的场地设计平面，仅是在场地为水平面条件下的最佳设计平面，显然，它不能保证在一般情况下总的土方量最小。