点状目标群渐进式抽象方法研究成果

杜晓初

(湖北大学资源环境学院，武汉市武昌区学院路11号，430062)

摘　要　点状目标群是地图中经常出现的一种空间分布现象，对这种目标群的分析和化简是空间分析和地图综合的重要内容。提出了一种基于Delaunay三角网的点状目标群的抽象方法，这种方法考虑了点状目标的可视性特征，保持抽象前后拓扑关系的一致性。

关键词　点状目标群，空间抽象，渐进式方法，拓扑关系

点状目标群是地图中经常出现的一种空间分布现象，对这种目标群的分析和化简是空间分析和地图综合的重要内容，在这方面有很多研究工作。Sadahiro提出了邻近(Proximity)、聚集(Concentration)和密度变化(Density change)三个因素来描述点状目标群的分布［1］;郭仁忠给出了空间目标分布的分布密度、分布中心、分布轴线和离散度等4个参数［2］;郭庆胜结合地图综合的特点，提出了一种考虑点状目标群与其他要素关系的分类方法，通过建立点状要素群外轮廓线的方法结构化点状要素群，并将这种方法用于点状目标的选取［3］;艾廷华利用Delaunay三角网和Voronoi图，给出了分布范围、分布密度、分布中心、分布轴线等描述点状目标群的4个参量，并结合这些参量建立了点状目标群的化简方法［4］。

显然，这些文献中提出的一些参数都是在矢量空间中进行描述的，也就是说，其中的点状目标是纯几何意义上的点，没有形状和大小之分。在这种情况下，点状目标之间的拓扑关系只有相离和重合两种，因此在进行选取和删除等抽象操作之后，点群之间的拓扑关系可以自然地保持一致。但是在很多情况下，我们需要在可视空间(地图空间)中对点状目标群进行抽象。由于人类视力的分辩能力有限，可视空间中的点状目标一般用点状符号来表示，这些点状符号有一定的面积，并且根据点状目标所表示的地理实体的不同，这些点状符号也有大小之分。这样，在进行点群目标的抽象操作之后，由于比例尺的减小，可能会出现点状目标之间的相互压盖，就出现了抽象过程中拓扑关系的不一致性问题。

为了在点状目标群的抽象过程中保持拓扑关系的一致性，必须考虑到抽象之后点状目标群的可视特性，目前地图综合中的移位操作主要就是解决这个方面的问题。尽管通过移位操作可以保持综合过程中拓扑关系的一致，但是如何通过计算机来自动实现这一过程，目前还没有一种很好的方法。为此，我们试图用Delaunay三角网的化简方法，实现可视空间中点状目标群的抽象。

1　点状目标群的抽象方法

为了保持点状目标群抽象过程中的拓扑一致性，我们必须考虑到每一个点状目标与其所有邻近点之间的距离，因此可以首先构建这些点状目标之间的平面Delaunay三角网。

1．1　Delaunay三角网的构建

Delaunay三角网是将平面中离散的点集按照一定的规则连接成的一种三角形网络，这种网络是由俄国数学家Delaunay首先提出，并证明了该网络中所有三角形的最小内角之和最大。因此，人们将这种网络称为Delaunay三角网。Delaunay三角网是Voronoi图的对偶图，其原始定义源于Voronoi图。

定义:设P={p1，p2，…，pn}(n≥3)是欧氏平面上的一个离散的点集，p为平面上的任意一点，d(p，pi)表示点p和pi(pi(P，且i= 1，2，…，n)之间的欧氏距离。定义到pi(i= 1，2，…，n)的所有距离最小的点p的集合，即

V(pi)={p/d(p，pi)≤d(p，pj)，j≠i，j= 1，Λ，n}

为pi生成的Voronoi多边形，其中pi称为生成元或者生成点。称最后得到的多边形集合V(P)={V(p1)，V(p2)，…，V(pn)}为点集P={p1，p2，…，pn}生成的Voronoi图。将有公共边的Voronoi多边形的生成点连接起来得到的三角形形成的三角网，如图1所示。

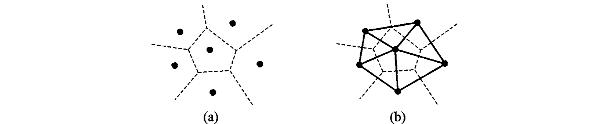
图1　Voronoi图和Delaunay三角网

Delaunay三角网具有以下性质:①Circle准则:也称空圆特性，即任意一个三角形的外接圆范围内不包含点集P中任何的其他点。如果一个三角形中包含其他的点，则此三角形不是Delaunay三角形，则重新建立三角形，直到满足Circle准则。②最大最小角特性:三角形的最小内角尽量最大，即三角形尽量接近等边。这个特性事实上与Circle准则是等价的。③唯一性:对于确定的点集(无四点共圆)，Delaunay三角网是唯一的。

建立Delaunay三角网有很多算法，最常见的有逐点插入法、三角网生长法、分治算法以及凸壳算法等。

1．2　Delaunay三角网的化简方法

在Delaunay三角网中，点状目标群的抽象问题转化为Delaunay三角网的化简问题。对于三角网的表达和化简，目前有很多方法，如Hoppe等提出和发展的渐进网格(Progressivemesh)表达和化简方法［5］;Schroeder等人提出的三角网内部点抽取(Decimation)化简方法［6］;Cohen等人用一种化简封套(Simplification envelope)来控制三角网近似化简的精度［7］。

尽管三角网化简方法很多，但是最基本的方法主要有两种，一种方法是三角网边(Edge)的缩减(Collapse)，也就是将三角网中的一条边抽象为一个点，从而简化该网络［5］，如图2所示;另一种方法对三角网中某一个顶点(Vertex)进行删除，形成一个多边形，然后交换(Swap)该多边形的对角线，形成新的三角网［6］，如图3所示。

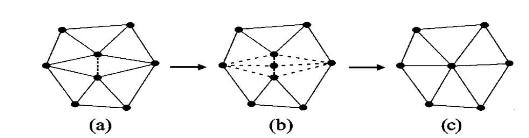
图2　三角网边缩减化简过程

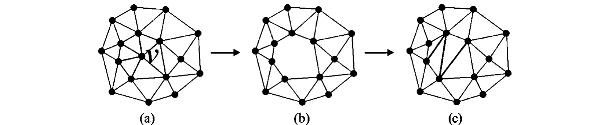
图3　三角网顶点删除化简过程

在这两种化简方法中，边缩减化简方法在原理和算法上都比较简单，并且能够更好体现渐进化简的思想，因此这里我们采用边缩减化简方法来对点状目标群进行抽象。

2　点状目标群抽象的数量特征

用三角网边缩减方法来化简点状目标群需要解决的首要问题是被缩减边的选取。目前大多数根据距离度量进行选取，Hoppe采用一种能量函数(Energy function)来对被选取边进行控制［5］。为了在抽象过程中保持点状目标群之间拓扑关系的一致，这里我们仍然使用欧氏距离作为缩减边选取的基本度量。主要考虑点状目标之间的距离、点状目标的影响区域大小以及影响区域之间的间隔三个数量特征。

2．1　Delaunay三角网各边的长度

根据渐进式化简方法的要求，首先必须选取Delaunay三角网中最短的边作为被缩减的对象，因此需要选出最短的边。由于点状目标群中每一个点的坐标是已知的，并且我们在平面空间中进行讨论，因此可以用下面的公式计算Delaunay三角网中任意一条边的长度:

其中，d(Ei)表示Delaunay三角网中任意一条边Ei的长度，边Ei对应的两个顶点为Vi1和Vi2，则Xi1和Xi2分别为这两个顶的点横坐标，Yi1和Yi2分别为这两个顶点的纵坐标。

2．2　点状目标的影响区域

在空间数据库中，点状目标一般是对空间实体的一种符号化(Symbolization)，而这些空间实体在现实空间中往往具有不同大小的面积;另一方面，在空间数据的表达空间中，这些点状目标也必须占有一定的空间。尽管我们可以忽略现实空间中点状符号所表示的空间实体的实际大小，用完全相同的点状符号来表示所有的点状目标，但是在表达空间中点状符号必须占有一定的空间，并且随着表达空间的缩小，这些点状符号所占有的实际空间会变大。例如，图4 (a)表示某一个表达空间中点状目标之间形成的Delaunay三角网，当其表达空间抽象为图4 (b)的大小时，由于点状符号不随比例尺的变化而变化，因此此时的点状符号之间的拓扑关系就不能保持原来的相离关系。如果将抽象后的空间恢复到原来的表达空间，则点状符号被放大，成为一个区域，如图4(c)中的圆形区域。为了讨论的方便，我们称这些圆形区域为相应点状符号的影响区域。

点状目标的影响区域大小取决于点状符号的大小和表达空间的尺度这两个因素:表达空间越小，其影响区域越大;点状符号越大，其影响区域也越大。对于相同类型的表达空间，点状符号的大小是确定的。

影响区域一般表示为以点状目标为圆心的圆，其大小用该圆的半径来表示，如果不考虑点状目标的语义特征，可以认为所有的影响区域大小是相等的。将点状目标群从比例尺为M1的表达空间抽象到比例尺为M2的表达空间时，影响区域的半径记为R(M1，M2)。设点状符号的半径为R0，则影响区域的半径R(M1，M2)可以用下面的公式进行计算:

(www.xing528.com)

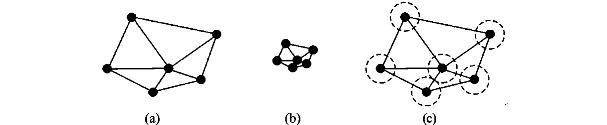
图4　点状目标的影响区域

2．3　点状目标影响区域的间隔

由于点状符号是对空间实体的符号化，因此在空间数据的表达空间中点状符号之间一般保持相离关系。为了在抽象过程保持点状目标群拓扑关系的一致，即各点状目标之间的相离关系，抽象后各点状目标之间必须保持一定的间隔，对于抽象前的点状目标而言，就是其影响区域之间必须保持一定的间隔，如图5所示。

图5　影响区域之间的间隔

影响区域间隔的大小与表达空间大小和人眼视力的分辩能力这两个因素有关。在这两种因素中，人眼视力的分辩能力是确定的，我们可以根据这一确定数值以及抽象前后的比例尺大小，来计算影响区域之间必须保持的最小间隔。设人眼视力对点状目标的分辩距离为T0，则从比例尺为M1的表达空间抽象到比例尺为M2的表达空间时，影响区域之间的最小间隔T (M1，M2)可以用下面的公式计算:

3　点状目标群的抽象

如前所述，点状目标群的抽象有很多方法，在这里我们采用渐进式抽象方法，这种方法的主要思想为:首先找出Delaunay三角网中长度最小的那一条边;然后根据影响区域的大小和间隔判断是否需要对此边进行操作;最后，如果满足条件，则进行缩减操作。重复该过程，直到所有Delaunay边都不满足缩减条件，则抽象过程完成。下面详细说明点状目标群的渐进式抽象过程。

3．1　Delaunay三角边的数据组织

Delaunay三角网的数据存储方式与离散点存储方式不同的是，它不仅要存储每个点的坐标，还要存储网点连接的拓扑关系、三角形及邻接三角形等信息。一般采用一种混合表示网点及三角形邻接关系的结构，它是在直接表示网点邻接关系的结构基础上再增加一个三角形的数表。在这里由于只需要计算Delaunay边的长度，因此可以只存储每个点的坐标和相应的Delaunay边。该数据可以用如表1所示的表格来表示。

表1　点状目标群抽象过程中的数据存储表

表1中记录了每一条Delaunay边的长度，其中，如果Ps和Pt是两个最邻近关联点，则有Ps Pt= Pt Ps。此外，在不同类型的表达空间中，点状符号的大小和人眼视力分辩距离有所区别，如在纸质地图中，点的直径为0．3mm(50cm距离)，相邻实心图形的间隔为0．2mm，因此在地图空间中可以取R0= 0．15mm，T0= 0．2mm。这样，就可以确定R(M1，M2)和T(M1，M2)的值。

3．2　点状目标群的抽象过程

点状目标群的抽象步骤如下:

(1)比较所有Delaunay边的长度，选出其中的最短边P I P J(如果有几条最短边，则取点标识号最小的那一条);

(2)若2R(M1，M2)+ T(M1，M2)＞d(PI PJ)，则退出操作，否则，进行步骤(3);

(3)若2R(M1，M2)+ T(M1，M2)≤d(PI PJ)，则将边PIPJ缩减为一个点P(1)，该点为线段PIPJ的中点，坐标为P(1)((XI+ XJ)/2，(YI+ YJ)/2);将原Delaunay三角网中P I和P J的最邻近点和P(1)联结，形成新的Delaunay三角网，如图2所示。

(4)重复以上的操作，直到所有的缩减操作完成。

4　讨论

显然，点状目标群的渐进式抽象方法有如下的优点:

(1)渐进式抽象的每一次操作都将其中的两个点进行合并，实现对点状目标群最小局部的抽象，并且每一次抽象操作完成以后都要对所有的点状目标群的总体分布情况进行考察，然后确定抽象操作继续进行，因此这种方法是一种动态的抽象方法，它能够很好地保持点状目标群的整体分布特征。

(2)这种方法是在保持点状目标群的可分辩特征的条件下进行的，能够保持点状目标群的离散特征，也就是保持它们之间拓扑关系的一致性。

(3)在渐进式抽象方法中，点状目标的影响区域和间隔需要根据抽象前后的比例尺进行计算，将点状目标群的可识别性与其抽象程度联系起来，可以直观地反映抽象结果与抽象程度之间的联系。

(4)这种抽象方法的计算原理、方法以及数据组织等比较简单，可以很方便地进行。

参考文献

［1］Yukio Sadahiro．Cluster perception in the distribution of point objects．Cartographica，34(1): 49－61，1997

［2］郭仁忠．空间分析［M］．北京:高等教育出版社，2001．

［3］郭庆胜．点状要素群的结构化及其在综合中的应用［J］．解放军测绘学院学报，Vol．16，No．3，Sept．，1999

［4］艾廷华，刘耀林．保持空间分布特征的群点化简方法［J］．测绘学报，Vol．31，No．2，May，2002

［5］Hoppe H．，Derose T．，Duchamp T．，Mcdonald J．and Stuetzle W．Mesh optimization．Computer Graphics (SIGGRAPH’93 Proceedings)，pp．19－26，1993

［6］Schroeder W．，Zarge J．and Lorensen W．．Decimation of trianglemeshes．Computer Graphics(SIGGRACH’92 Proceedings)，26，2: 65－70，1992

［7］Cohen J．，Varshney A．，Manocha D．and Turk G．．Simplification envelopes．In Proc．Of ACM Siggraph’96，119－128，1996