A.B.Murray模型和R.Thomas模型简介

11.2　A.B.Murray模型和R.Thomas模型简介

作为开拓者，A.B.Murray^［6，7］和R.Thomas^［8］成功地将元胞自动机引入河流动力学以及河床演变学领域，本节对他们的研究成果分别进行评述。

11.2.1　A.B.Murray模型

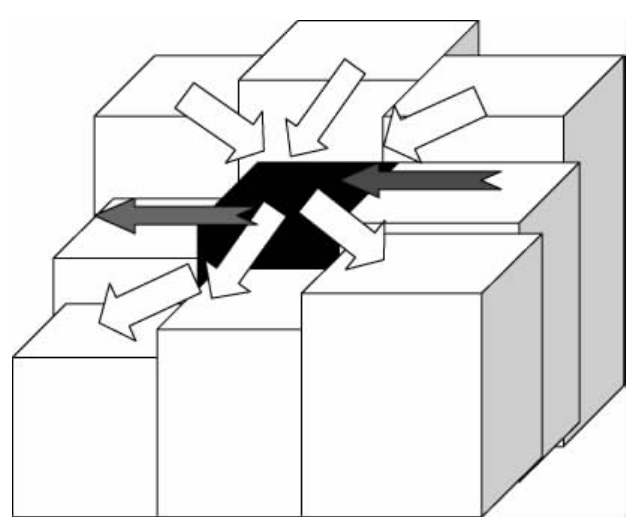
图11-1　元胞邻居定义（白色箭头为水流方向，灰色箭头为床沙运动方向）

1994年，A.B.Murray和C.Paola率先推出了一个辫状河流的元胞模型，开创了河型数学模型的新纪元。Murray在如下假设的基础上构建了元胞模型：

（1）元胞及状态

Murray认为元胞分别代表水流、河床以及床沙。其中河床和床沙是可相互转化的。

（2）邻居定义

采用了标准Moore型八邻居定义（图11-1），具体使用时不考虑回流，每个元胞的水流流向下行三个元胞。床沙运动为左右移动。

（3）演化规则

A.B.Murray在水流运动规则和泥沙运动规则上作了深入的研究。其中水流运动规则为：

或

其中，式（111）和（112）中的系数n，结合水力学公式计算为0.5。(www.xing528.com)

辫状河流具有复杂的泥沙运动规则，A.B.Murray由简单到复杂，依次构造了六种泥沙输移模式：

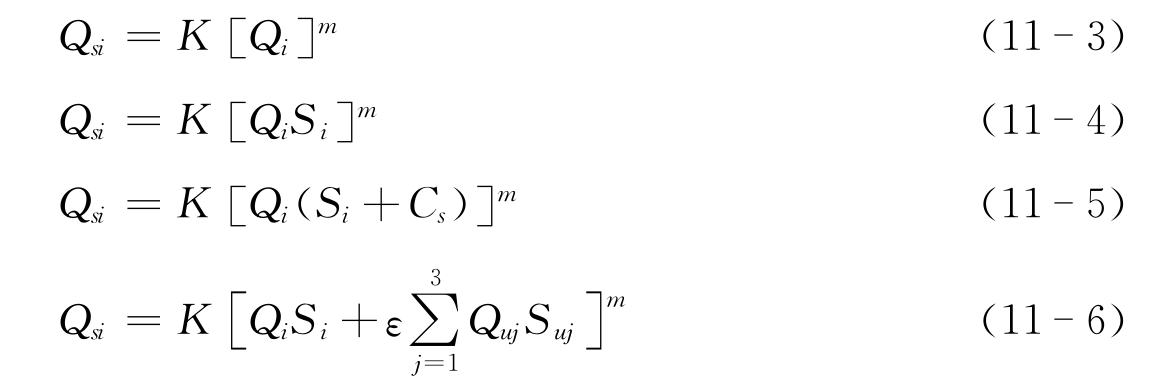
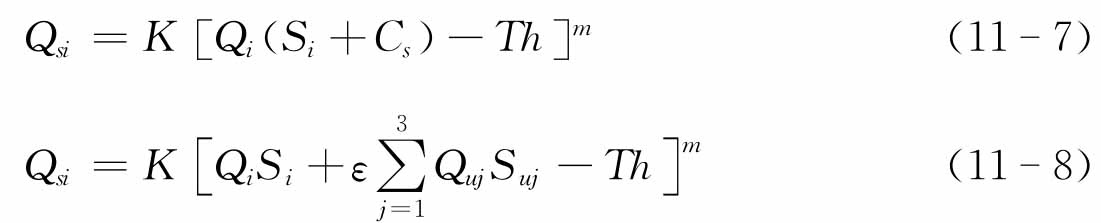
此外，A.B.Murray还对模型时间等问题作了探讨，图11-2为A.B.Murray模型的部分模拟结果。由图可见，A.B.Murray使用简单的数学模式，成功模拟了复杂的辫状河流发育。

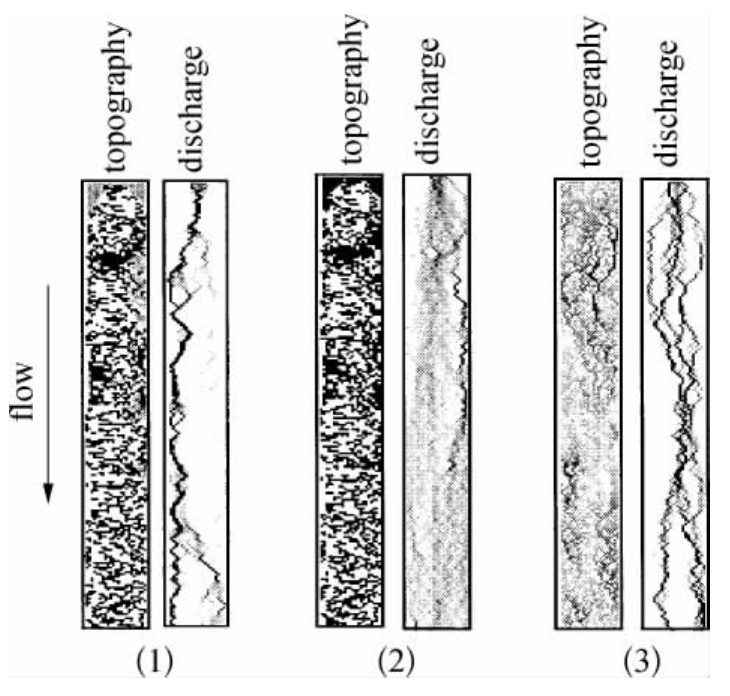
图11-2　A.B.Murray模型的部分模拟结果

11.2.2　R.Thomas模型

R.Thomas在A.B.Murray模型的基础上作了一些改进：（1）在A.B.Murray模型的邻居定义中，一个元胞下邻三个元胞，因此水流和河槽的夹角最大为45°，但天然河流中许多超过了45°。Thomas定义了一个新的邻居结构，一个元胞下邻五个元胞。（2）对水流运动规则作了大幅度的改动，采用了两套模式：校准模式和非校准模式。计算组式分别为：

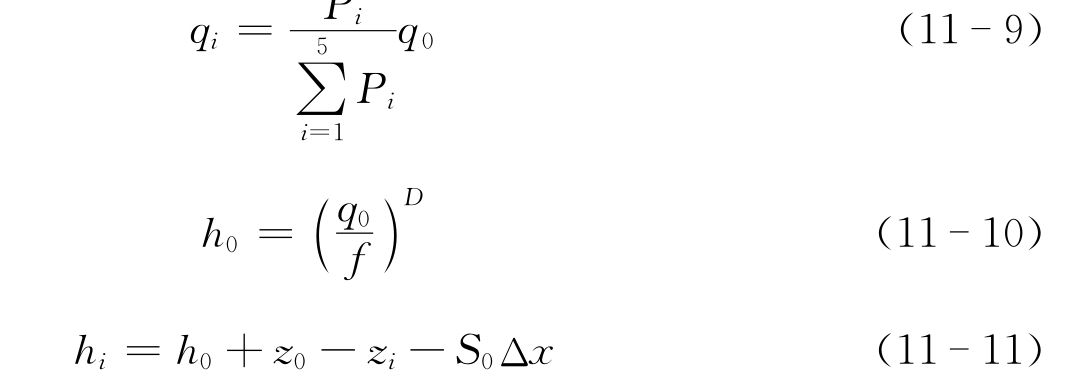
和

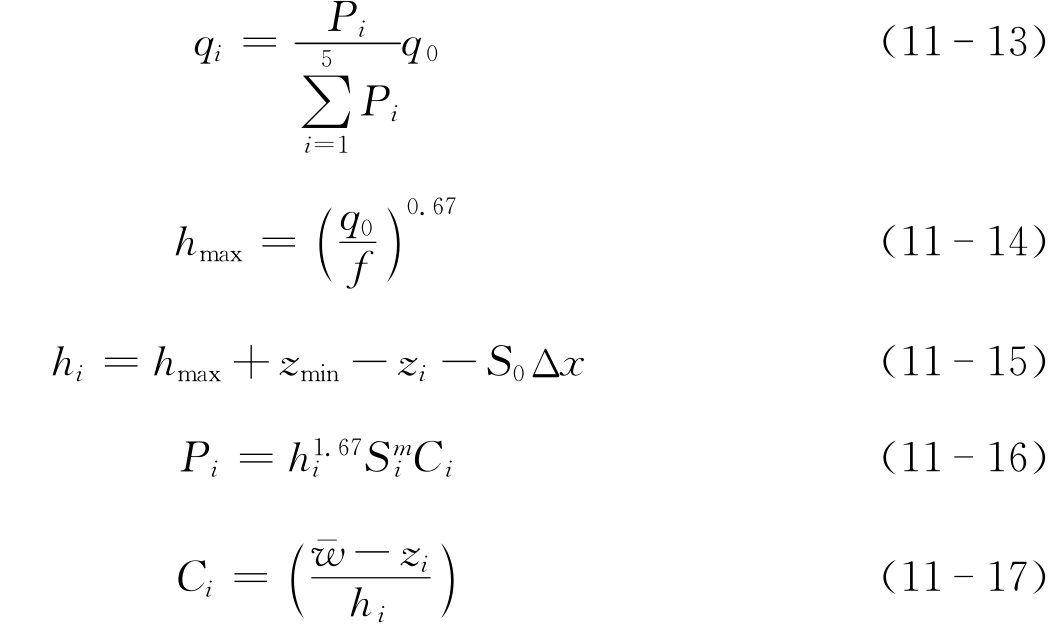
Thomas模型是一个水流模型，改进之后在模拟辫状河流中的水流分布上获得了较大的成功。甚至与较成熟的传统水流模型Hydro2de（基于Navier-Stokes方程构建）计算结果比较，尤其在局部水流中具有优势。图11-3为Thomas模型模拟的辫状河流水流分布，体现了较好的模拟效果。

图11-3　Thomas模型的部分模拟结果