元胞自动机简介及应用实例

10.2　元胞自动机简介

元胞自动机是一种时间、空间、状态都离散，空间上的相互作用及时间上的因果关系皆局部的网格动力学模型；很容易直接描写单元间的相互作用，不需要建立和求解复杂的微分方程（只要确定简单得多的单元演化规则即可），所以非常适合于模拟单元间有强烈耦合与协调作用的非线性系统的自组织过程。

近年来，元胞自动机方法在地理学如城市扩展、灾害评估方向、交通流问题上得到了较为广泛的应用^［13］。元胞自动机模型真正开始应用于河流动力学研究，最早的当属Murray和Paola^{［14，15］}，作为开创者，Murray不仅成功建立了辫状河流的元胞模型，还解决了诸如离散时间等基础性问题。R.Thomas^［16］在前者的基础上建立了一个改进的元胞模型，较好地模拟了辫状河流的水流过程；Hans-Henrik Stolum^［17］研究了弯曲河道的自组织过程。

10.2.1　元胞自动机的基本思想和特征

一个元胞自动机模型中，体系被分解成有限个元胞，同时把时间离散化为一定间隔的步，每个元胞的所有可能状态也划分为有限个分立的状态。每个胞在前后时间步的状态转变按一定的演变规则来决定，这种转变是随时间不断地对体系各胞同步进行。因此一个胞的状态受其邻居胞的状态的影响，同时也影响着邻居胞的状态。局部之间互相作用，相互影响。通过这一定的规则变化而整合成一总体行为。以简单离散的元胞来考察复杂体系，这是很有用的思想方法。

我们用二维元胞自动机来进一步说明上述思想。二维元胞自动机中，一个元胞可取为规则的正方形胞、三角形胞或六方胞。下面以正方形胞来说明。在这种体系中对一个胞的邻居关系结构有两种考虑^［18］：

（1）四邻居关系，它只包括4个第一近邻胞，这种邻居关系也称为von Neumann型邻居关系。

（2）八邻居关系，如图10-1，它还包括了4个第二近邻胞，因此周围共有8个邻胞，它也称为Moore型邻居关系。相应于von Neumann型邻居关系的元胞自动机规则可描述为：

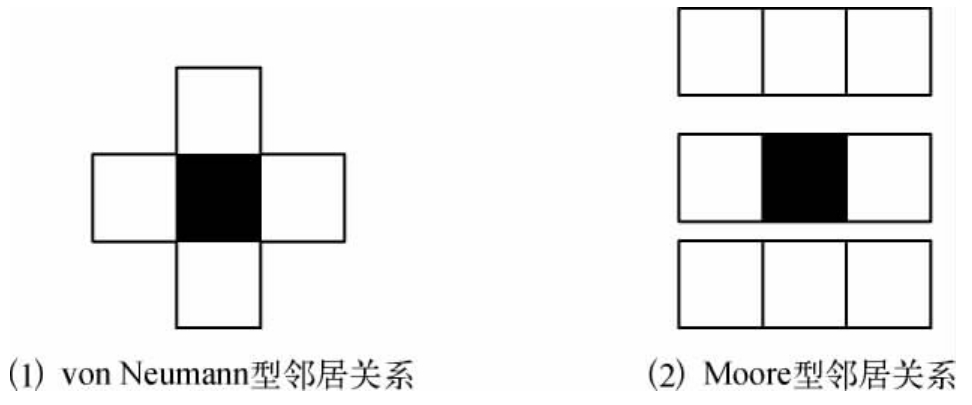
图10-1　二维元胞自动机体系中正方形胞的两种邻居关系

元胞自动机的演变规则基于局域交互作用，可以很简单，而反复迭代实施的结果往往能产生十分复杂的结构。下面以“生命游戏”（Game of Life）为例来说明。将一个矩形的体系划分为许多的小正方形胞以代表细胞，每一个胞的生存状态用一个变量来描述，如图10-1所示，0表示死，每个胞的生存状态与其周围的8个胞的生存状态有关，一个胞的状态依赖于周围胞的状态变量的总和。若一个胞周围有三个胞为生，则该胞始终保持为生，即该胞若原先为死，则转为生，原先为生则保持不变。如果一个胞周围有二个胞为生，则该胞的生死状态不变，其他情况下，则该胞始终为死。这样一个简单的基于局部作用的规则在计算机模拟实施时却演变出了十分丰富多样的复杂结构，甚至再现一些复杂的生命现象^［19］。事实上，自然界确有这样一种生存规律：一个生命若周围的同类生命太少的话，会因得不到帮助而死亡；若周围的同类生命太多，又会因相互竞争得不到资源而死亡。“生命游戏”对此规律作了高度的抽象简化，是一个十分典型的元胞自动机模型。图10-2为“生命游戏”中的几个图片片段。

图10-2　生命游戏

10.2.2　元胞自动机的唯象描述及基本特征

Wolfram就不同的初始态和不同的演变规则进行了大量的计算机模拟试验，考察了对结果的影响并利用已有的理论进行了分析，较系统地提取出元胞自动机的一些规律及基本的特征^［20］。根据演变的终态特征，他把元胞自动机定性地分为四大类：

（1）演变为唯一的最终均匀状态，它常常很快就可达到，少数情况存在较长的过渡；

（2）产生分离的时间序列上周期性的简单结构，每个结构为稳定的或具有很小的周期的振荡，元胞自动机规则能过滤掉一些复杂的结构，仅把初始态的一些简单的形态保持下来，而且产生的也是简单的形态；

（3）产生非周期性形态，并表现出混沌行为，它们常以一恒定速度向各个方向生长，产生较对称的形态；

（4）表现出复杂的局域的不规则生长形态，常出现许多持续的结构，其中一些在不断地传播开来，二维中确切的这类元胞自动机比较少，比一维中少得多，它常伴随第三类发生且其特征常会被第三类元胞自动机所覆盖。

同一类中的所有元胞自动机不论其演变规则如何，定性上都表现出相似的行为。

10.2.3　元胞自动机的优点

将元胞自动机应用于建立水系和河流数学模型，首先是因为元胞自动机模型具有如下的优点：

（1）元胞自动机是天然的空间动力学模型，适于模拟具有时空的空间复杂系统。(www.xing528.com)

河流乃至一切地理事实、地理现象，既包括了在空间上的性质，又包括了时间的性质，只有同时把空间及时间这两大范畴纳入某种统一的基础中，才能真正认识其基本规律，从而完整认识其复杂性。元胞自动机是一个典型的天然空间动力学系统，其时间是一个离散的无限集，所以不仅能够模拟和预测系统的长期行为，关键它还能模拟系统的动态行为过程。元胞自动机在模拟空间现象在时间和空间上的动态变化时的直观、生动、简洁、高效、实时等特征是其他模型如系统动态等所难以媲美的。因此，在水系和河流发展的模拟方面，元胞自动机有其内在的合理性。

（2）元胞自动机“自下而上”的构模方式，符合复杂系统的形成规律机器研究方法。

从方法论看，元胞自动机不是用很繁杂的方程从整体上去描述一个复杂系统，而是由系统构成单元的相互作用来模拟复杂系统的整体行为。元胞自动机采用的是典型的“自下而上”的构模方法，这是大多数复杂系统研究方法所采用的思维方式，是复杂性科学所倡导的复杂性研究方法，只有从系统元素的状态和行为入手，模拟它们的相互作用，才能从根本上解决复杂性问题。

水系、河流的发育从根本上讲也是一个复杂性问题。以往从资料分析以及实体试验研究等手段，都是宏观上的研究。基于元胞自动机的水系、河流数学模型的建立，有助于从微观上开创一个崭新的研究领域。

（3）元胞自动机强大的复杂性计算能力，适于模拟系统的复杂行为。

元胞自动机具有计算的完备性特征，可以模拟非线性复杂系统的突现、混沌等特征，是模拟生态、环境、灾害等多种高度复杂的地理现象的有力工具。具体讲来，它的复杂计算能力主要体现在它的计算完备性特征和突现计算功能上。

1）计算完备性。元胞自动机在构造和计算上的简单性，丝毫没有限制元胞自动机模拟复杂现象的能力。有关元胞自动机计算能力的研究表明，已知的每一个图灵机都可以用元胞自动机。目前已经构造出有14个状态（即k＝14）的通用元胞自动机。它可以模拟任何一个元胞自动机在任何初始构形时开始的动力学行为^［21］，计算的完备性在理论上保证了元胞自动机模拟复杂现象的可行性。

2）突现计算功能。突现的概念来源于系统论，指系统（或整体）在宏观层次上拥有其部分或部分的加和所不具有的性质。突现性可以理解为由局部的相互作用可以带来系统整体的表现行为，如宏观吸引等的发生、稳定结构等在时空中的演化等^［22］。当把河流看成一个系统时，河型转化就是一种突现。元胞自动机的转换函数虽是局部和简单的，但却能够在整体上表现出许多周期、混沌、信息传递、自复制等复杂的突现行为和现象，因而它能对生态、环境、灾害等多种高度复杂的地理系统进行高强度的仿真。同样也应该能模拟河型转化的突现现象。

此外，元胞自动机还有易于应用计算机构造模型，在空间数据结构上易于与遥感、地理信息系统等地理信息技术集成等优点，在河流动力学和地貌学研究领域的前景也相当广阔。

10.2.4　建立元胞模型

与标准元胞模型相比，水系、河流元胞自动机模型有其现实的地理背景，因此构造水系、河流元胞自动机模型，首先要解决以下几个方面的问题。

（1）元胞及状态

在标准元胞模型中，元胞是一个有限、离散的集合体，每个元胞的状态取其中的一个值，并不一定有具体的物理含义。在水系、河流的元胞模型中，鉴于其现实的地理背景，我们必须赋予元胞及其状态以相应、具体的地理含义。如水系元胞及状态不仅要考虑单位面积的产流因素，还必须反映地形、地质因子，甚至必须进一步细化到植被影响、土地利用类型影响等等。此外，水系元胞模型研究的是水系和流域，河道与地表之间的区别、坡流和河流的区别、大河与小河的区别也应该在元胞及其状态中体现。河流元胞模型主要研究河道，因此河道的滩、槽、河岸等等，也应该在元胞及状态中体现。具体的元胞模型，根据研究目标的不同，元胞及状态也需要重新定义。

（2）元胞空间

标准元胞模型中的元胞空间是一个抽象的离散值，而水系、河流元胞模型中元胞空间必须为一个确定的值。空间外形应当为四方形、六方形或者是三角形中的一种，且具有确定的度量大小。如水系元胞模型中的河流级别、河流元胞模型中的水深等。

（3）邻居定义

标准的元胞空间中，元胞的邻居常被定为平衡对称的构型，鉴于地理实体间相互作用的复杂性，河流元胞模型的定义应更加灵活。首先，毫无疑义，此时元胞的邻居关系与水流方向有关，这一点与研究森林火灾的“林火模型”^{［24，25］}相似。此外，如果河床有横比降，邻居关系还应进一步改变。

（4）演化规则

演化规则是元胞自动机的核心，它决定了元胞自动机的动态演化过程，在地理学元胞研究中，演化规则集中体现了空间实体间的相互作用，这种相互作用根据不同应用而被赋予不同的地理涵义，可以说，地理学元胞研究中的规则是地理特征在局部和微观上的体现。

水系、河流的元胞模型，和其他元胞模型一样，确定演化规则具有基础性的意义。演化规则的合理与否，直接决定了模型模拟的准确程度。

（5）离散时间

标准的元胞模型中，时间概念是一个离散尺度，也是一个抽象的时间概念。水系、河流的元胞自动机模型的时间概念在与标准时间对应的同时，还必须与现实的年、月、日等实际时间度量概念相对应。