河流自然模型时效的研究成果

6.3　河流自然模型时效的研究

在众多的河流自然模型试验中，试验水槽规模不等、流量不均，试验目的各异，试验时间也不相同。短的如Fridekin^［1］的试验时间仅12小时，而尹学良^［7］的试验长达2 300小时。为保证试验精度，满足试验目的，模型的规模和试验条件均得到了精心的设计；而试验时间多由经验确定，或语焉不详，试验的时效缺乏合理的分析和理论的支持。

在我们进行的水库下游再造床过程中河型转化的概化水槽试验（以下简称概化水槽试验）中^［1719］，曾对自然模型试验的时效进行了一些探讨。这里结合该试验及前人的试验成果，对自然模型的时效作进一步的研究。

6.3.1　河流自然模型的时效

我们将河流充分发育所需的试验历时，称为时效。时效的重要性在河流自然模型研究中是毋庸置疑的，时效决定了试验时间的选定。

自Fridekin^［1］开始，许多学者通过河流自然模型试验开展了研究工作，比较著名的有Schumm、尹学良、唐日长、Smith等人，这些河流自然模型的共同特征为：在均匀可动沙体中，人为塑造规则初始河道；试验开始注入一定流量水流，水流自由造床；通过人为改变河床组成、水流条件（来水来沙）、比降（河谷比降）、河槽边界条件等，研究河流的演变过程和演变结果。

由于试验条件和研究内容的不同，试验时间也有较大的差异。我们的概化水槽试验，原理和构造与前人相同；以下试验资料除注明外，均为该概化水槽试验数据。试验概况比较如表6-8。

表6-8　河流自然模型试验概况

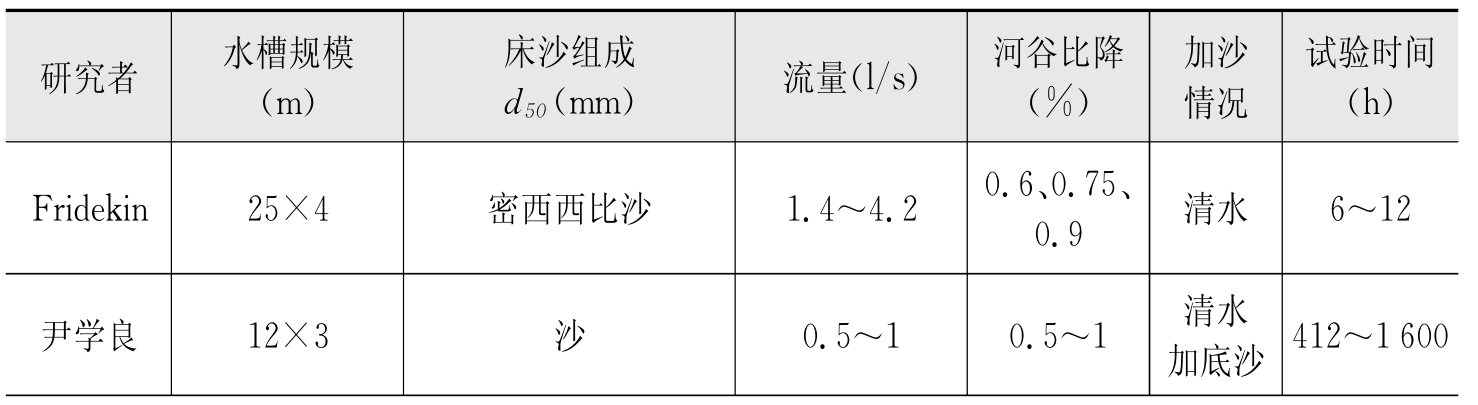
（续表）

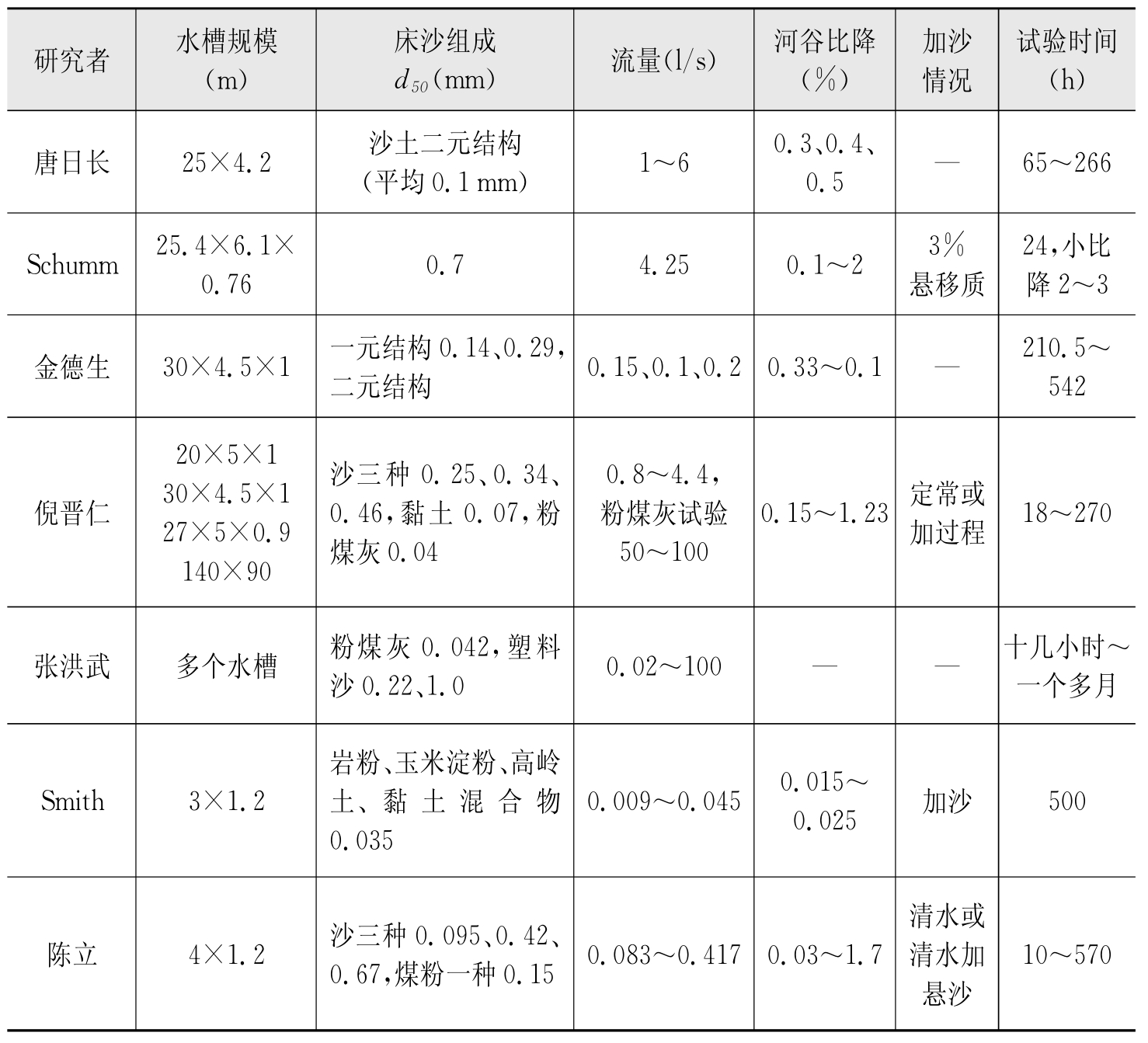
注：资料依据引用文献，当有多组试验数据时，采用文中较主要组次数据。

天然河流是不断运动的，其塑造形成一般都有一个漫长的历史过程。试验河流的发展也是一个较长期的过程，尤其是清水造床，河道对河岸的侵蚀和扩展甚至是永无终止的（取决于抗冲覆盖层的形成）。试验时间过短，河道形态没有完全确定，得出的结论不一定正确；试验时间过长，试验周期和设备的要求增加，且无论多长的试验时间与天然河流发育漫长的地质年代相比也是极短的，过长的试验时间也失去了模型试验的意义。

河流动力学认为：随着外界条件的变化，河流有一个自调整过程；当这个过程完成之后，河流将达到一种动态平衡状态；几乎所有的河流自然模型都是建立在这样一个理论的基础上：河流的自调整作用会导致一种动态平衡。自然模型时效的实质就是河流状态达到了动态平衡时的试验历时。

迄今为止，模型的时效或者说动态平衡状态的确定还是基于经验的基础上，较多地应用了基于目测和主观决定的指标，如：岸滩的侵蚀、河势较长时间的稳定、底沙运动状态等。这增加了试验结果判定的不确定性。如Schumm^［3］认为，大比降时只要24小时河道已经基本稳定，小流量甚至只需2～3小时。而尹学良^［7］认为Tiffany^［2］和Friedkin^［1］试验时间只有12小时，时间过短，所造成的河线形式难说稳定；在尹的试验中，试验条件不同的组次之间出现第一个边滩时间从3.5小时到128小时不等，河道发育较慢组次出现第一次切滩的时间几乎与较快组次的全部试验时间相等。这种试验条件不同所需时间不同的现象较为普遍（参见表6-8），而所有的试验都缺乏时效的合理性分析和验证，试验时间差别较大。

6.3.2　时效的影响因素

6.3.2.1　时效的影响因素

河流自然模型的时效至今没有定论，从模型河流发展历程分析，应与河床的稳定性、水流同河床的相互作用以及河道的发展过程有关。关于前两者，目前的研究成果比较多，也有比较成熟的结论^［21］。尹学良^［7］将三者结合起来，提出了河床可动性的表达式：

式中ρ、ρs分别为水及泥沙的比重，d为河床泥沙粒径，含有黏性土时应考虑黏性的影响，J为比降，Q、T分别为该流量级的大小及历时。（6-2）式中的T与本书中的时效并不是同一概念，但却包含了相同的影响因子。根据时效的定义，达到动态平衡时河床的可动性Z将趋于一个较小的定值，将（6-2）式变形为：

（6-3）式中以t代替T，而且不采用等号是因为：时效t和历时T不具有等价性；而（6-3）式更多地只是表明了一种趋势性的相关关系，而非确定的关系式。由式可知，当河床可动性Z趋于定值时，所需的时间t与Q、J成反比，与d成正比。这一点与多次试验结论是一致的，其理论基础在于：来水来沙和比降等条件决定了河道的外部能量，流量和比降增大时，水流造床能力增大，河槽变形加剧，河道形态变化加速，但达到相对平衡的时间普遍增大；河床组成等边界条件决定了河床的内部构造，同种天然沙组成的河槽，中值粒径较大者河床较稳定，达到动态平衡的时间较短。

在概化水槽试验中，我们每隔几个小时测量试验河道岸线的位置，并将岸线变化速率为1mm／10h定为一个临界值，作为决定试验时效的一个重要指标，当岸线变化速率小于该值时，认为该河道是趋于稳定的。图6-4为各组次试验河道岸线变化率达到临界值时的历时小时数，图中趋势也证实了（6-3）式反映的趋势关系。

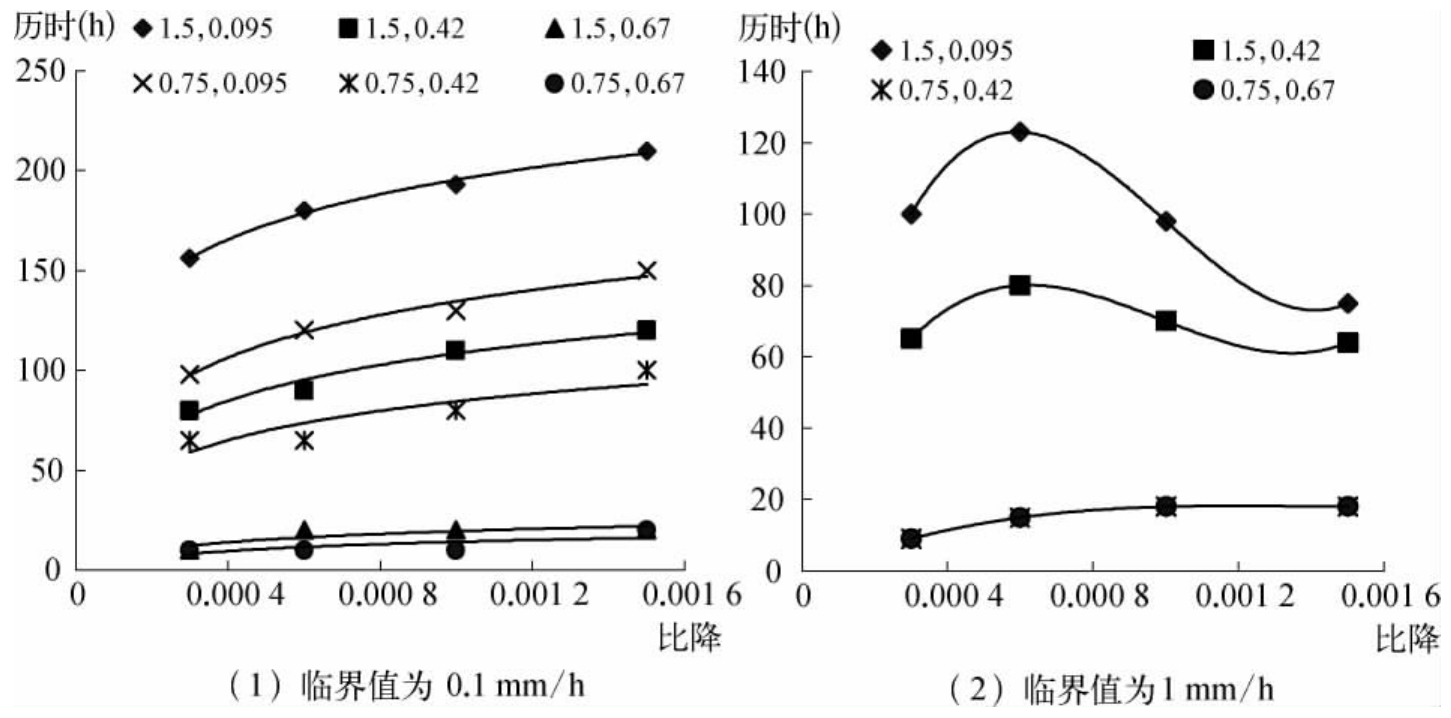
图6-4　河岸变化速率达到临界值的历时（系列数值分别为流量m³／h、床沙中值粒径mm）

6.3.2.2　时效判定指标的选择

在前人的试验中，判定试验性时效的常用指标主要有岸线变化率（即岸滩侵蚀度）、河势较长时间的稳定、底沙运动情况等；通常以相对较长试验时间，经验判定而得到。这种判定方式一方面要求一定的经验和判断能力，可信度难以保证；另一方面，即使在一定时段河道变化较小，也不能完全保证试验的时效，在河流自然模型试验中，往往有特例发生。如概化水槽试验组次E11-1（图6-5），图中可知，随着试验的进行，河岸变化由快变缓，试验进行到7-3小时之后，河岸变化极小；此后71小时中，河岸变化速率最大仅1.87mm／10小时；到144小时左右，河岸变化率突然增加，整体河道形态也随之改变。试验E11-1的这种突变现象的产生是有特殊原因的：该试验初始河道为曲折型，73小时以后，上游左岸形成了一个抗冲露头（如图中加注），这个顶冲位置使得随后河床变化率较小；试验进行144小时左右，顶冲位置被冲开，河床变化率随即迅速增加。

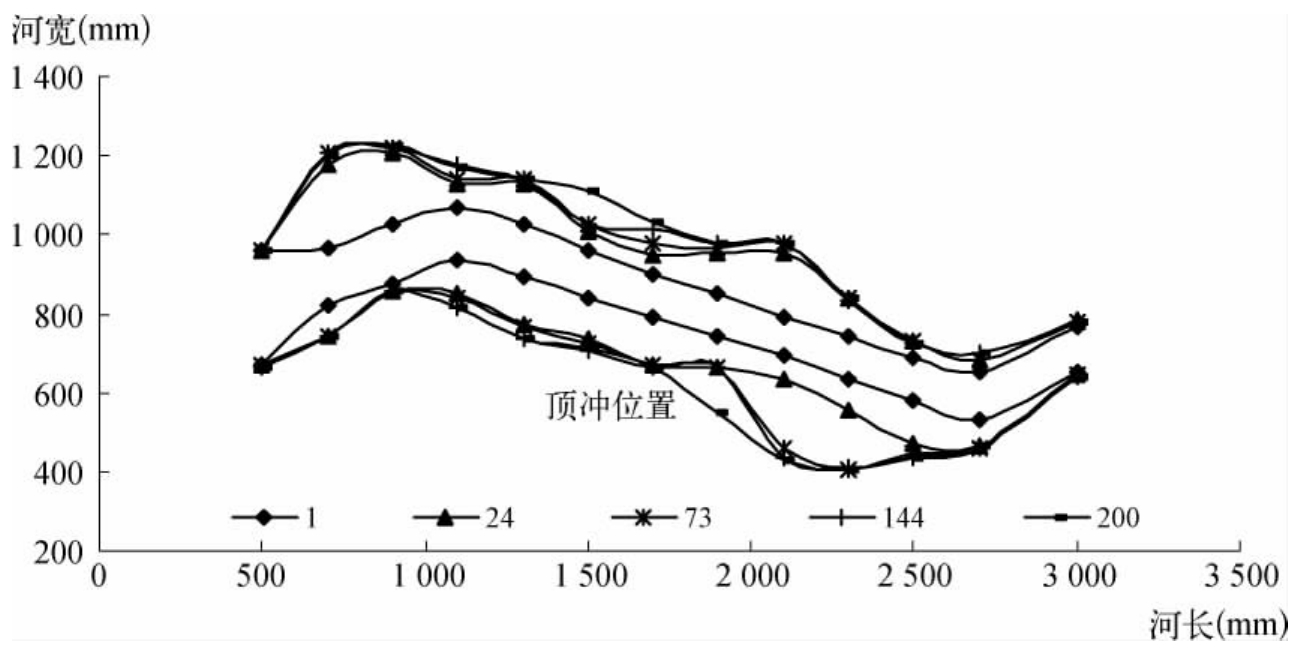
图6-5　E11-1河岸线位置变化（历时单位：小时）

试验E11-1等特例在河流自然模型试验中并非绝无仅有。另一方面，即使河道达到动态平衡时，其滩槽变化幅度也可能较大，如弯曲河道自身的弯曲和裁弯过程。两方面都增大了时效确定的难度。为保证试验的时效、保证模型试验结果的正确性，必须在常用指标的基础上，对试验时间进一步进行分析和验证。

6.3.3　相似理论在时效验证中的应用

河工模型包括定床模型和动床模型，目前在理论上已较为成熟，实践上也在生产和科研中得到了广泛的应用。从本质看来，河流自然模型也是河工模型的一种。相似论是模型试验的理论基础，满足相似条件时，模型与原型是相似的，此时可以用模型试验的成果来推断原型的情况。同理，确定了相似条件，原型的变化情况也能对模型的变化状态进行预估和判定。基于这个思路，可以运用河工模型的方法来验证河流自然模型的时效。

6.3.3.1　计算原型与模型的选择

采用20世纪60年代下荆江人工裁弯河道作为原型。因为下荆江河道为典型的弯曲型冲积河流，河床多由沙土和粉土组成，与河流自然模型试验具有一定的相似性。人工裁弯具体过程为先开挖断面较小的引河，过水后引河逐渐发展，最终发展为新河，原河道逐渐淤废，最终变成牛扼湖，发育过程也与自然模型类似。

谢鉴衡^［20］对下荆江裁弯作了较为系统的研究，并进行了裁弯后的水力学及河床变形计算，认为在裁弯进行之后的四五年，引河展宽过程已基本结束，冲刷大致终了。将谢文中裁弯后中洲子河段作为计算原型。

计算模型采用概化水槽试验中试验A6-3-1和A7-3-1。计算原型与模型概况如表6-9。

表6-9　计算原型及模型概况

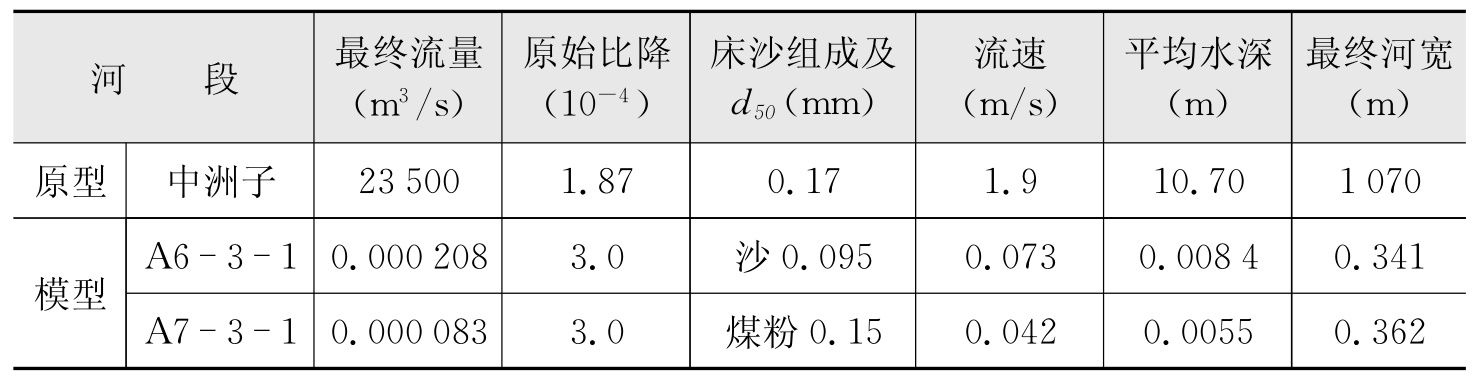
6.3.3.2　计算方案及结果(www.xing528.com)

根据相似理论，以6年为原型变化时间，推求模型时间。计算方法如下：

（1）平面比尺λ_L、垂直比尺λ_H

（2）流量比尺

（3）流速比尺

（4）时间及河床变形比尺

其中

采用两种计算方案（表6-9）：

A.以流量为相似指标，反推平面比尺，再求出时间比尺；

B.以最终平均河宽为相似指标，算出平面比尺，再求时间比尺。

通过时间比尺将模型时间转换成原型时间，再和原型实际时间对比，计算结果如表6-9，其中模型历时为岸线变化率＜1mm／10h时的小时数。

表6-9的计算结果表明，所选模型折合原型的历时与实际原型的历时还是有较大差别的。这种差别主要有两个原因：

（1）计算时间比尺的（6-6）、（6-7）式中仅考虑了λρ的影响而没有考虑d 50的影响。因此采用模型沙A7-3-1的计算历时远比采用长江沙的A6-3-1的计算历时更接近原型实际历时。而A6-3-1的d 50仅为0.09 5mm，远较荆江床沙中径为小。

（2）模型流量固定，而原型引河流量是逐渐增加的。中洲子河道第一年的引河流量为15 800m³／s，仅为最终流量23 500m³／s的67.2%，较小流量的造床能力偏小，时间较长。

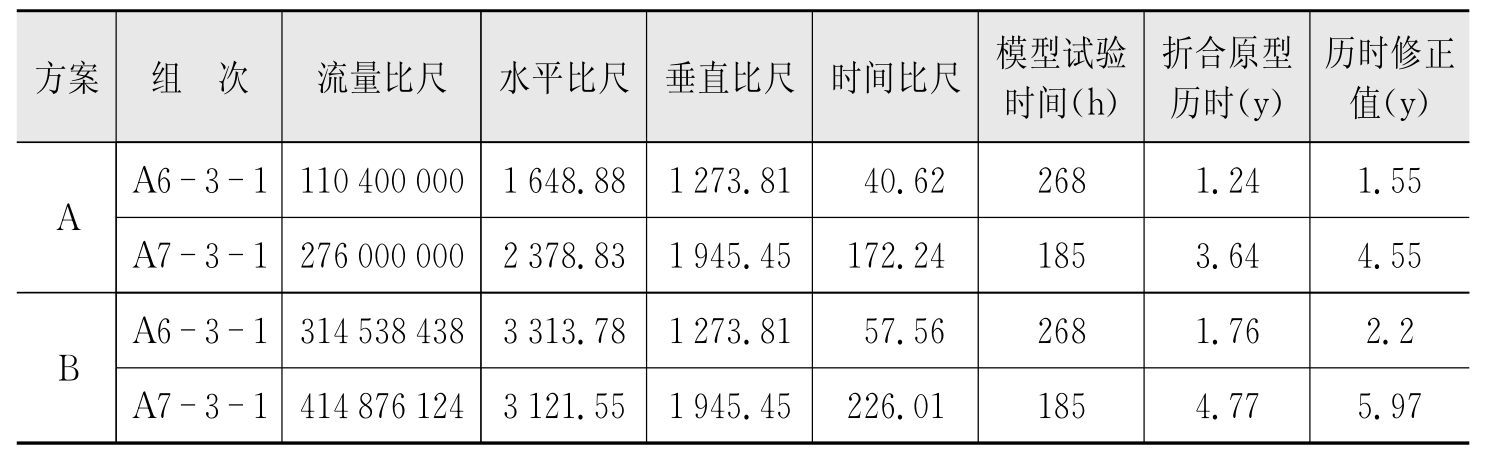
表6-10增加了以平均流量19 6 50m³／s为造床流量计算修正历时，计算结果表明，模型历时与原型的时间具有一定的相似性。

表6-10　相似理论计算结果

严格说来，河流自然模型“是不满足相似论的基本要求的，在理论上存在缺陷”^［21］。但在确定自然模型的试验时间时，选取适当的原型进行参照，也为一可行之道。

6.3.4　“空代时”假说的验证

6.3.4.1　“空代时”假说

“空代时”假说是现代地貌学的基本理论之一。“空代时”假说认为：在特定的环境条件下，对空间过程的研究和对时间过程的研究是等价的；在缺少绝对数量方法的情况下，有时可以认为地貌空间集合体可以代表地貌体的时间序列。

“空代时”假说在地貌的研究中取得了较大的成功。如Davis^［22］在很大程度上基于“空代时”假说创建了侵蚀循环学说；Lobeck发现从华盛顿山到大西洋海岸这一剖面中，地貌的发育体现出明显的阶段性；Ruhe和Savigear^［24］对野外资料的研究表明，地貌体确实存在时、空替代现象——在空间上分布的不同类型可以推演到时间序列上，代表地貌发育的不同阶段。用空间变量代替时间变量曾为一种非常流行的解决地表过程长期演化的地貌学方法。

在自然河流演变过程中，“空代时”假说也同样可以在相当的范围内解释许多现象，有时候现象甚至还比较直观，如丹江口水库兴建后，清水下泄引起河道冲刷的现象。河道的冲刷在时间上有个逐步粗化的过程，空间上冲刷范围有由上而下逐渐推进的趋势，时间和空间的现象具有较明显的相似性。这时用“空代时”假说来描述和预测有较好的效果。

6.3.4.2　自然模型试验中的“空代时”现象

对比前人以及我们的概化水槽试验成果发现：在河流自然模型试验中，时间与空间的相似性更为确定和明显。图6-6为试验A811的河床平面演变过程图。由图可知，随着时间的变化，河道有顺直到弯曲最终变为微弯的变化过程，这与河道空间上由上而下的纵向变化趋势基本一致，此时空间和时间的变化可认为是可以相互替代的。

这种空时变化的状况在自然模型中是非常普遍的。张欧阳^［25］引入“空代时”假说分析游荡河流造床试验过程中河型的时空演替和复杂响应现象时，不仅证实了自然模型试验过程中，河流的时、空演替过程可以相互代替，而且具体提出了水深、曲率、比降和效能率的时空相似。

必须指出，“空代时”理论在地貌学中并不是一个非常可靠的理论，空间和时间尺度的不确定性和野外资料的缺乏使得该理论的使用相当危险，甚至受到多方面批评。而河流自然模型试验则不存在这些缺陷：时间和空间的具体性、原始河槽—调整—平衡这一完整的发展过程都构成“空代时”理论成功应用的基础，因此该理论的引入将在时效的定性判定中提供判定指标，使之具有更理想的可信度。

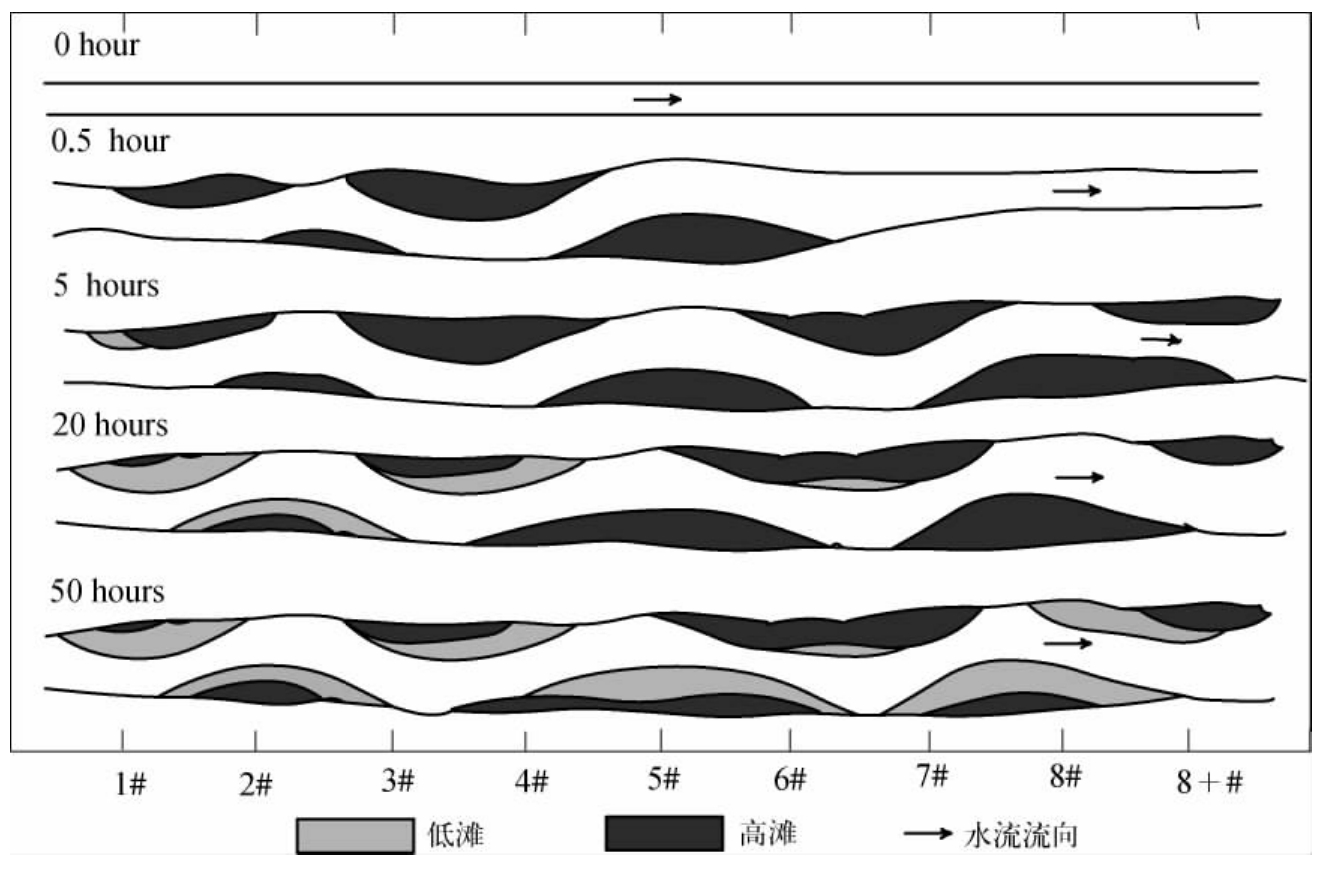
图6-6　试验A81-1的河床平面演变过程略图

将“空代时”假说反映的趋势用在自然模型的时效的验证当中是非常直观而有效的。如Schumm^［4］关于顺直河流的试验（图6-7）：试验进行几个小时后，河槽首部塑造了几个弯道，但下游却为顺直型；Schumm以此时的试验现象作为依据，得出了“在一定的边界组成下，只要初始坡降没有超过某一界限值，河流可能发育成顺直型”的结论。这个结论普遍被认为是不可信的，正如倪晋仁^{［16，26］}指出：照片中的河道形态远非最终河道形态，随着试验时间的推进，下游的顺直河道形态也难以维持；Schumm试验历时过短，河流没来得及调整是其缺乏可信度的主要原因。

运用“空代时”假说分析图6-7可以较直观地得出结论：在空间范畴内上游有河槽由顺直形成弯曲河道的事实，时间范畴内下游河道也应有逐渐由顺直向弯曲河段转化的趋势，在下游河道没有完成其演变时终止试验，时效是不能保证的。

图6-7　Schumm关于顺直河流的试验照片

“空代时”假说不仅有助于模型试验的定性判定，如能对时间尺度和空间尺度相似关系作进一步研究，将有助于河流自然模型试验时效的定量确定。