汉江中下游平原河流的弯道演变与转化

2.3　平原河流的合理弯道形态——以汉江中下游为例

天然河流中，弯曲河流是最常见的河型。几乎不存在超过10倍河宽的直河段。在自然条件下，弯道是不断发展的，因而其河床形态也在经常变化，但是在河湾的发展过程中，具有某种形态的河湾却有相对的稳定性，它和其他形态的河湾比起来具有更多的出现机会，出现以后维持的时间也较长。这种河湾不仅变化小，河床形态也比较规则，水流平顺，滩槽水位差比较小。这种弯道形态在河道整治中常常被人们用来作为整治的典范，我们称之为河道最佳弯道形态。

河道最佳弯道形态的确定至今缺少有效和通用的方法。在航道整治的工程实践中，人们往往采用寻求优良的弯道作为典型的方法，来确定河道最佳弯道形态，这种方法，可靠性往往难以保证。

结合丹江口水库下游汉江航道整治工程的实际，我们对汉江中下游最佳弯道形态的确定进行了初步的研究。

2.3.1　弯道的平面形态

单个弯道的弯曲程度是沿程变化的，但在一定的范围内常近似为圆弧形，因而可用圆弧的半径R来表示其弯曲的程度，这一半径称为曲率半径R，其倒数为曲率。曲率最大的地方为弯顶，某一弯段进出口间包围的圆心角为中心角θ。包含两个弯段和过渡段的相应点之间的直线距离称弯距或河弯跨度L_m，相邻两反向弯顶间的横向距离为摆幅T_m，沿河槽长度和沿河长度的比值称为曲折率（图2-2）。

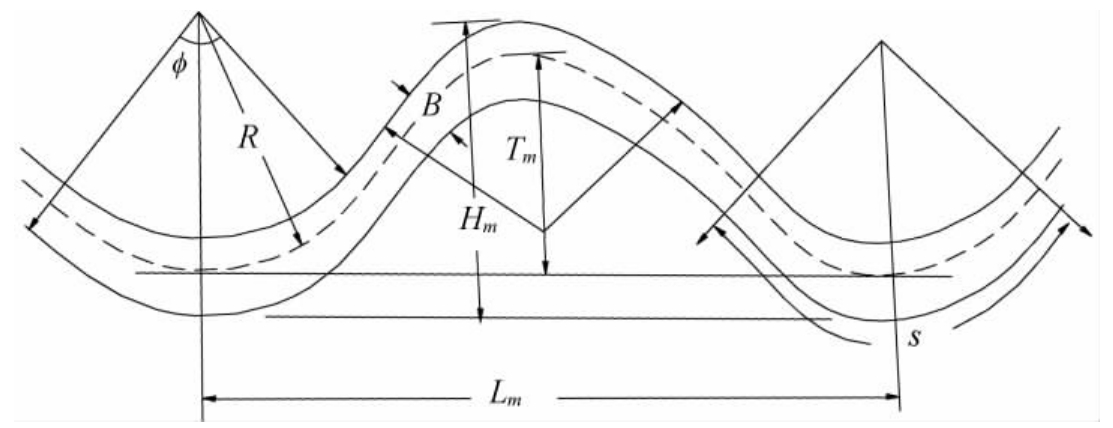
图2-2　弯道基本要素

人们往往用弯曲半径、中心角、弯距等基本特征值来表示河湾的平面形态，对于稳定河湾而言，它们与直段河宽的关系一般为^［1］：

2.3.2　最佳弯道形态研究

2.3.2.1　研究现状

河流弯曲的原因至今没有定论，Langbein通过随机游移模式，认为河湾最可能出现的流路相当于：

近年来，Hans-Henrik Stolum^［2］在G.Parker和E.D.Andrews等人的研究基础上，从分形的角度，研究了弯曲河道的自组织过程。这些研究揭示了弯道发育的几何过程，但对于河流弯曲形成和发育的力学机理仍缺乏明确的结论。

通常认为，最佳弯道形态与河道尺度、流量大小有关。钱宁^［1］在统计了多条河流数据的基础上给出了L_m与平滩流量Q_平的关系式：

欧阳履泰^［3］在一般的力学原理基础上认为河曲的发育和稳定与运动水体的切向惯性力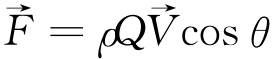有关。并根据水流阻力曼宁公式及连续运动原理，认为曲率半径R由反映水流动量的流量Q和比降J决定：

并结合部分弯曲河段的实测资料，得出了曲率半径R与流量、比降的经验关系式：

张笃敬^［4］运用上下荆江各河湾实测资料，经过相关分析，得到荆江河湾主流线弯曲半径的经验关系式：

必须指出，水流动力轴线的曲率与河槽的曲率是有较大区别的。当流量为平滩流量时，可以近似认为水流动力轴线即为河槽曲率。因此我们对（2-9）作适当变形如下：

（2-9）式较（2-8）式多了一个流量的函数H，从物理意义来讲两式是比较相似的。

上述公式结构较简单，但多数是局部河段的纯经验公式，使用范围受到限制。此外，弯道是水流与河床相互作用的结果，只考虑水流动力而忽略河床条件的做法是值得商榷的。Schumm^［5］统计了一些美国河流资料，认为随着河床和河岸组成物质中粉黏土含量的增大，河湾跨度有减小的趋势：

其中M为河床和河岸组成物质中粉黏土的含量。Chitale^［6］曾根据42条河流的实测资料，得出了如下经验公式：

其中D为床沙代表粒径。该式表明：河床组成物质越细，断面越窄深，河流也越曲折。

2.3.2.2　最佳弯道形态的推求(www.xing528.com)

最佳弯道形态，从理论上讲应该包含曲率半径R、圆心角θ，其余参数如河弯跨度和摆幅等均可由两者推求。一个较稳定的弯道形态，圆心角不能太大，畸弯无论从河势角度还是从航道角度来讲都是不利的；过小的圆心角则不易形成平顺的曲流流态。统计国内外多条河流的弯道形态，我们认为圆心角的合理范围在60°～180°之间。

最佳弯道的曲率半径首先与水流动力条件有关，这一点既可得到理论上的证明；“小水坐弯、大水趋直”，天然河流也提供了大量的实例。此时考虑动量的（2-9）式远较（2-8）式合理。

最佳弯道形态与河床组成物质的关系较为复杂。首先是不同的河床组成物理性质不同，难以找到确切代表其物理特性的统一指标，如许炯心^［7］认为砂质河床与砾石河床在物理力学性质上表现出很大的差异，服从不同的规律：砾石河床由非黏性粗颗粒构成，故床沙的临界起动切力与床沙粒径成正比。砂质河床的情形则较复杂，在重力占优势的范围内，床沙临界切力与粒径成正比；当粒径减小到一定程度，使黏性力占优势，则床沙的临界切力与粒径成反比。

最佳弯道形态是水流条件和河床周界条件相互作用、相互协调最终达到动态平衡的特征结果。因此，可以认为对于特征水流动力条件时，河岸和水流条件之间处于一种力平衡状态，包括了切向和径向：即水流切向力（τ₁）等于河岸的抗冲性，径向水流对河岸的压力（F₁，为向心力、科氏力等水流压力之和）等于河床的稳定性。即

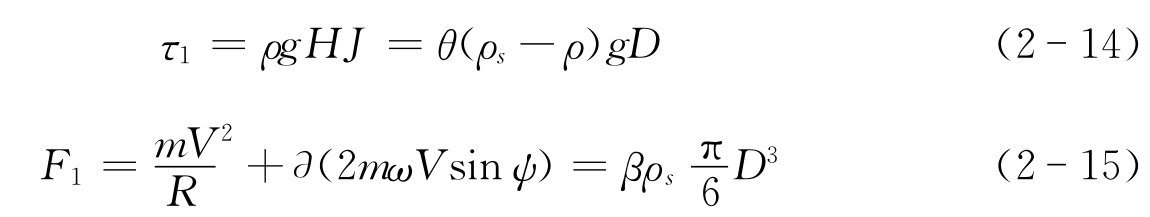
其中ə、β、θ为系数，与具体河道条件有关。当切向或径向力不平衡时，河湾蠕动发展，河湾外形将发生变化。根据天然河湾的变化特点，Hooke^［8］建议用河湾的折点和顶点的运动轨迹及中轴线方向的变化来区分河湾外形的变化，并归纳为下列基本类型：延伸、平移、旋转、扩大、侧向移动和复杂变化（图2-3）。由图可见，延伸和平移分别是径向和切向力不平衡的结果，其他类型均是由两种基本类型衍生。

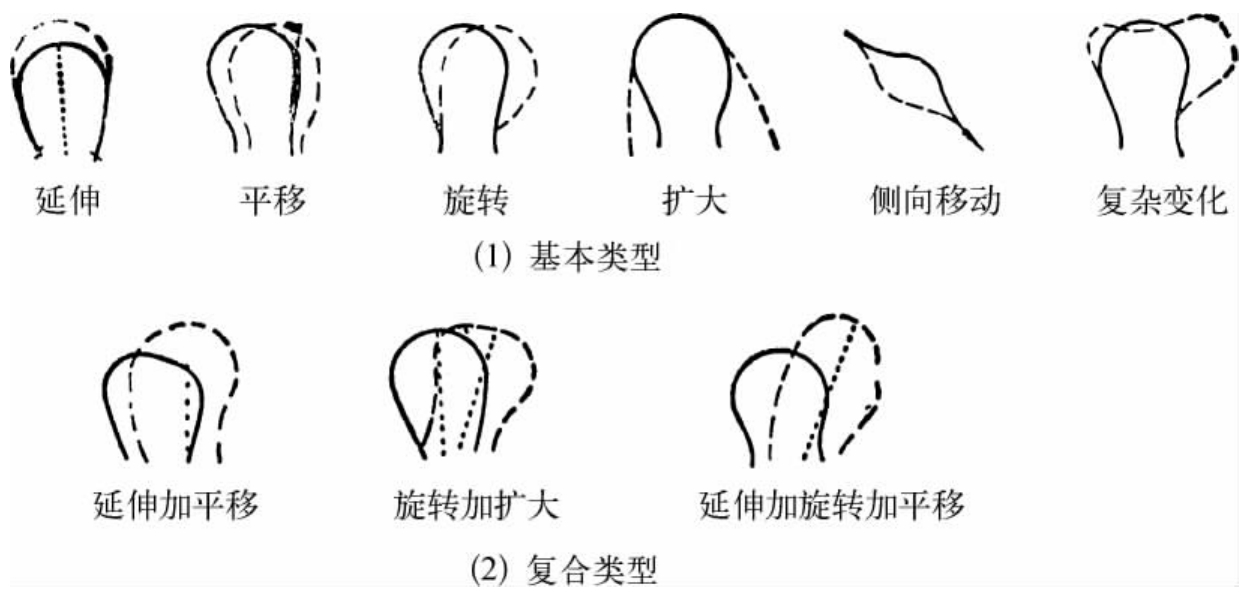
图2-3　河湾变形的基本类型（钱宁，1989）

在公式（2-4）、（211）、（212）的基础上，结合前人成果，我们认为最佳弯道曲率半径符合：

其中D为河床组成代表粒径。它当为松散颗粒时取中值粒径，为黏土夹沙时取相当的松散沙体中值粒径。概化水槽试验是探讨河流规律的有效手段，自Friedkin J.F.以来，Schumm、Smith、陈立等人均进行了弯曲河流的塑造尝试^［9］。（216）式反映的变化规律与这些水槽试验成果在定性上是一致的。只是由于水槽试验较多地着眼于反映河流曲折程度的弯曲度而普遍缺乏曲率半径的具体数值，因此要将（216）式进一步量化，还有待于更多的天然河流实测资料和水槽试验研究成果。

2.3.3　汉江中下游最佳弯道形态分析

2.3.3.1　最佳弯道形态的推求

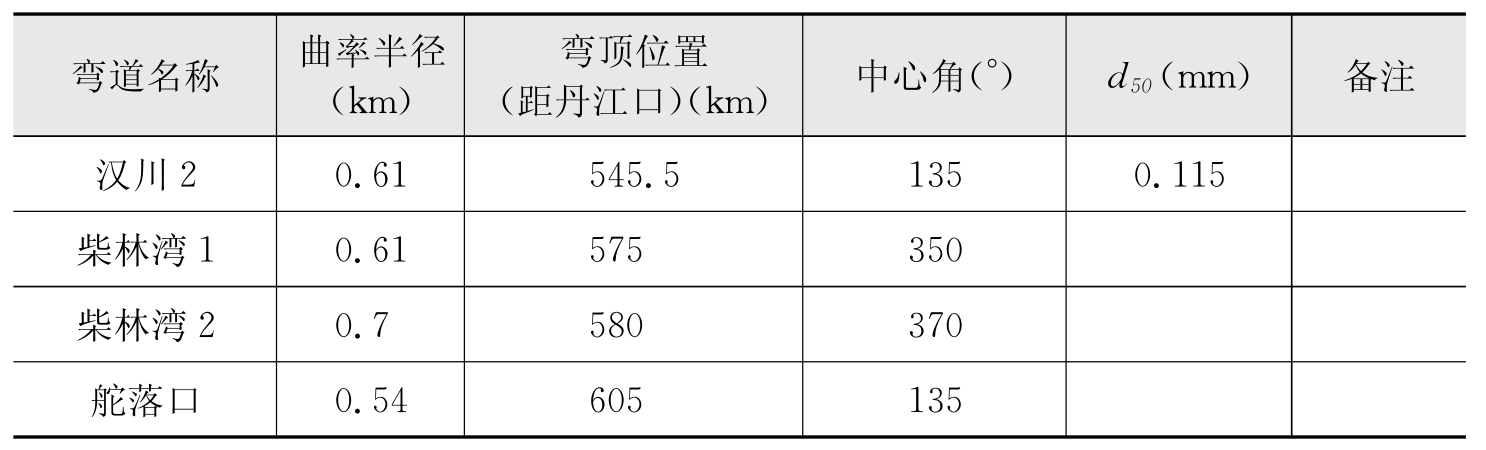
我们分析了丹江口水库以下汉江中下游31个典型弯道（表2-1）。这31个弯道可以分为如下三类：

表2-1　汉江中下游典型弯道概况

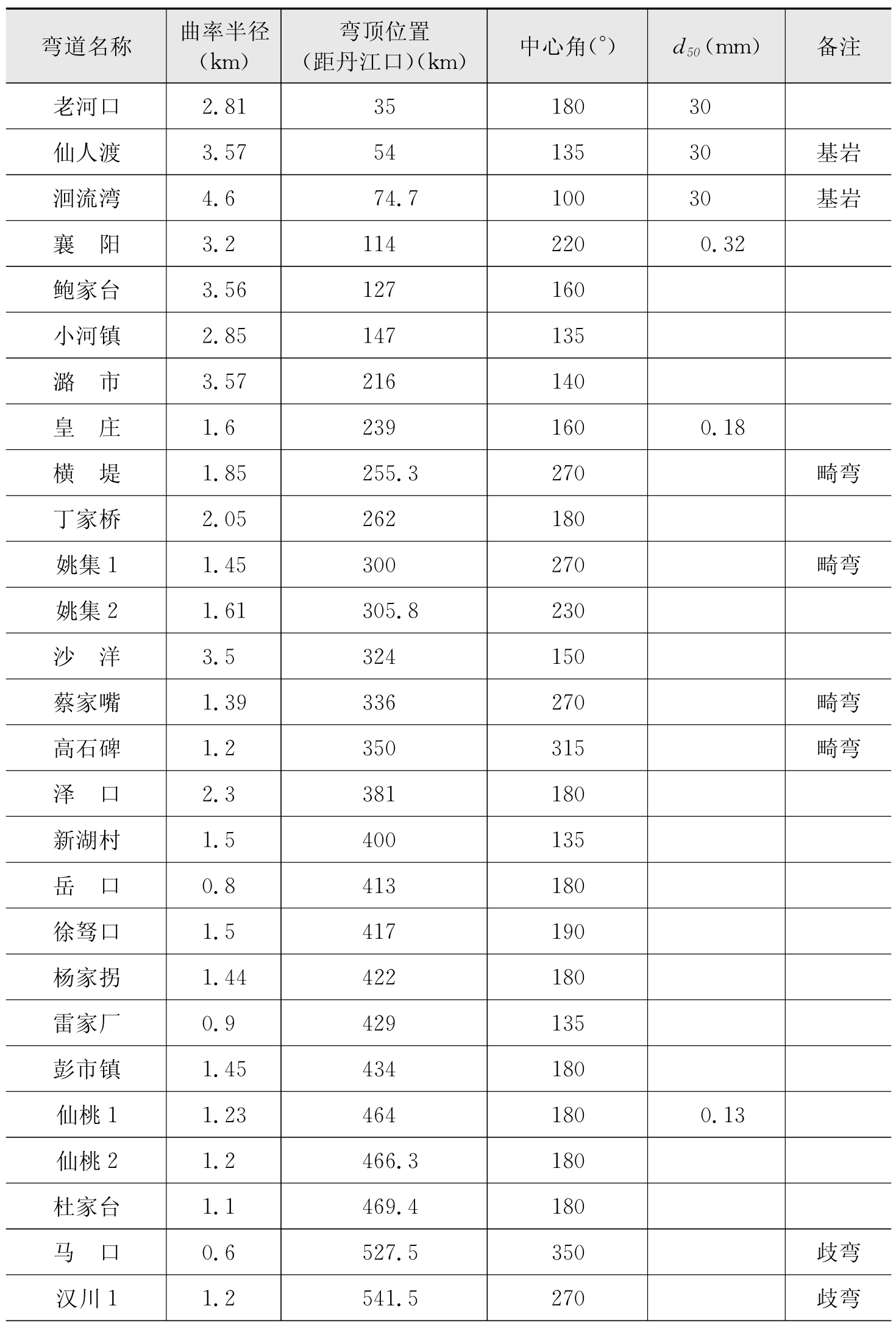
（续表）

（1）限制弯道。由于边界条件的限制，这种弯道往往没有发育成较规则的圆弧，顶冲点水流作用较强，主流线相对不平滑，有较明显的拐点。这类弯道一般曲率半径较大，如近坝段的仙人渡弯道、洄流湾弯道，下游的沙洋弯道等。

（2）正常弯道。这种弯道河床河岸组成一般比较均匀，因此可能形成较规则的圆弧，主流线平滑，水流平顺，中心角一般在180°左右，一般有连续数个弯道衔接。当进口和弯顶控制较好时，这类河湾稳定性较强；但控制较差时可能发育成畸弯。图2-4为仙桃附近弯道河势。

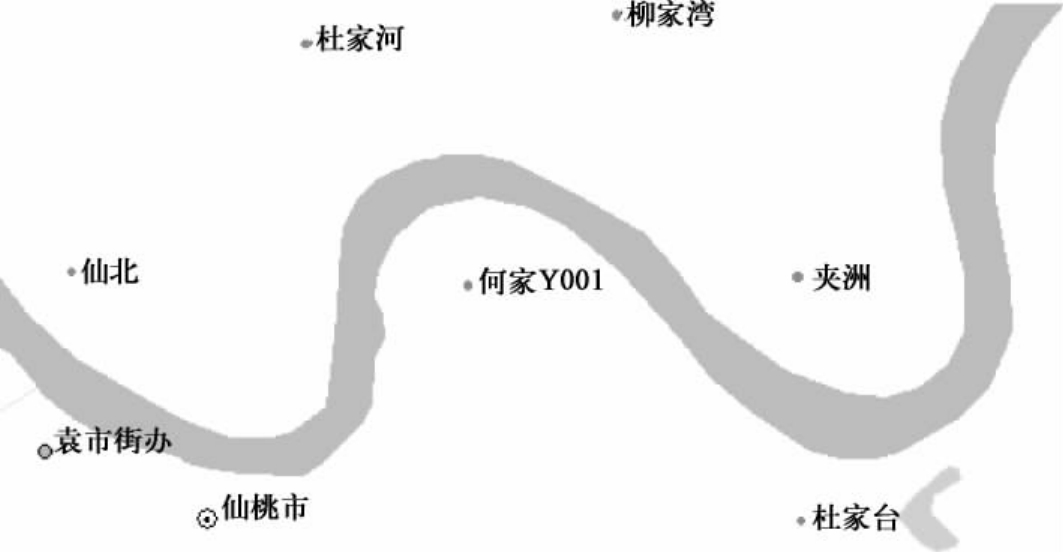
图2-4　仙桃附近弯道河势

（3）畸弯。这类弯道中心角一般在230°以上，河湾九曲回肠，对水流的宣泄和航道运输均不利。

结合汉江中下游弯道实际，引入（2-16）式，经适线得出汉江中下游最佳弯道形态的经验公式为：

该公式对于汉江中下游水利工程和航道工程中弯道形态的确定具有一定的参考价值。见图2-5。

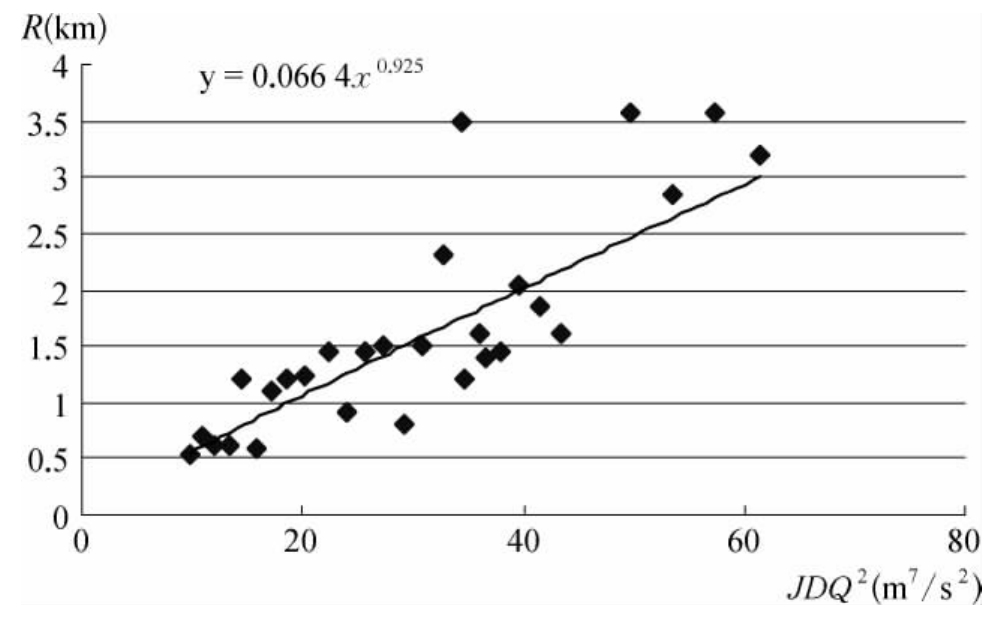
图2-5　汉江中下游R-JDQ²

2.3.3.2　建库后汉江中下游的撇弯切滩初步分析

丹江口水库兴建之后，汉江中下游发生了频繁的撇弯切滩，如近坝段仙人渡浅滩，1968年丹江口水库蓄水运行后发生撇弯切滩，江中形成一个大沙洲，1978年除原来的左右两汊外，在右汊之右又形成了另一汊道，从而形成三汊两洲的格局，至今仍维持此格局；在皇庄到泽口河段总计13个弯道中，有11个先后发生了撇弯切滩。

谈广鸣^［10］统计和调查后发现，汉江中下游的撇弯切滩有整体撇弯（切滩）和局部撇弯两种形式：整体撇弯即主流线从弯道进口段便开始向凸岸偏移，靠凸岸下行，弯曲半径变小；局部撇弯则是主流线下移，在弯道上段凹岸淤出新滩，弯曲半径减小。

据丘凤莲^［11］的研究，丹江口水库兴建后，汉江中下游的造床流量减小；河床质普遍粗化，但襄阳以下河段变化较小。综合分析汉江中下游的多个撇弯切滩的弯道，我们发现，襄阳以上河道，河床粗化程度大于造床流量变化程度，弯道变化趋向曲率半径增大为主；襄阳以下河道，河床粗化程度小于造床流量变化程度，弯道变化趋向曲率半径减小为主。但这一规律并不显著，说明在向最佳弯道形态的发展过程中，河道具有复杂的调整过程。