马克思主义社会科学研究方法论的统计资料汇总

一、统计资料的汇总、统计表、统计图

统计工作者为了从经验层次上证实自己在研究中所建立的概念、假设和理论，一方面是要正确地收集资料和数据，另一方面是要学会正确地处理这些数据。从统计的过程来看，统计资料地收集到整理的初始状态都是杂乱无章的，它可能分散在各个问卷及统计样本中间，也可能分散在其他统计结果和统计资料中(档案、文献、年鉴等)。因此如果对统计资料不进行有效的加工，统计就毫无价值。对核对无误的原始资料做初步的整理，就是对这些资料按一定的标准进行分类和和汇总，使之条理化、系统化。

1.统计资料汇总及其组织形式

统计资料汇总是指对调查所获得的原始数据资料的总汇归类。主要汇总方法有两种：手工汇总和计算机汇总。手工汇总是采用人工划记法或采用卡片法把抽查所得数据一一登录、分组和计算。但现在对大规模的调查来说，手工汇总已经难以胜任，需要借助计算机来完成，所以，现在普遍应用的统计资料的汇总方式是计算机汇总。计算机汇总是把原始资料转变为计算机可识别的数据的过程。计算机在社会调查研究方面的应用日益普及，各种统计软件也应运而生。

统计资料汇总的组织形式也称纵向汇总方式，是指按一定的统计管理体制，将统计资料自下而上进行汇总的方式。常用的统计资料汇总形式为：逐级汇总、集中汇总、综合汇总。

逐级汇总是按照一定的统计管理机制，将统计调查资料自下而上逐级汇总并逐级上报，直至最高机构。我国现行的统计报表制度主要采用这种汇总形式，一些专门调查也常采用这种形式。

集中汇总是指将统计调查资料直接集中到组织统计调查的最高机构或某一级的统计机构或部门统一汇总，可分为：越级汇总和超级汇总。越级汇总是指在自下而上的汇总过程中，越过一定中间层次而进行的汇总，介于逐级汇总和超级汇总之间。超级汇总是在自下而上的汇总过程中，越过一切中间层次，将统计调查资料由基层直接上报到组织统计调查的最高机构统一汇总。

综合汇总是将逐级汇总与超级汇总两种形式结合使用的方式。即将各级所需要的最基本的统计指标实行逐级汇总，同时又将全部原始资料集中到最高机构超级汇总。

统计汇总技术称横向汇总法，是指将同级单位的同级调查资料进行汇总的方法。它分手工汇总技术与计算机汇总技术。手工汇总技术是指运用笔、纸、算盘或小型计算器作为计算工具，对统计资料进行汇总的方法。计算机汇总技术即运用计算机软件进行汇总的方法。

统计汇总的步骤：设计汇总方案、汇总前的审核与处理、数据录入、归集资料并汇总、汇总后的审核。

2.统计表

所谓统计表就是用表格形式来表示变量的数值分布。它不需要文字叙述就能反映出资料的特性以及资料之间的关系。广义地说，统计分析所使用的一切数据表格均称为统计表。统计表是表达统计资料数量特征及关系的重要形式，因此在编印、传递方面有很大的优点。

统计表必须具备的内容有：

表号：统计表(×·×)或(×—×)。

表头：包括标题、时间、单位。

标志行：其中第一项为变量名称，第二项为变量对应数的说明。

主体行：出于变量取位的不唯一性，这部分至少要有二行以上。第一项位置，按列填写变量的不同取值，取值的顺序可以任意，这一项又称主词。第二项位置，按列填写变量取值相应的频次、百分比等。有时为了阅读的醒目，也可将频次和百分数都列在一张表上。这时，一般第二列排频次值，第三列排百分比，第二项以后的内容又称宾词。对于只有百分数的统计表，要写明统计总数。

表尾：如果引用的是间接资料，要写清资料来源。

一般说来，问卷调查表中可供选择的答案就构成了主体行中变量的取值内容。可供选择的答案数目就是主体行中变量取值的数目。例如性别有两种可供选择的答案：男和女。因此主体行中的变量值也就是男和女两行。但是有关意愿、原因的社会调查中，可供选择的答案类别数目，有时与变量值的数目并不相等。

例如如果有人同时挑选了两个答案，那绝不能分别在两类中各统计一次，这样就破坏了变量取值必须互斥的要求。正确的做法是将挑中两类答案的人，另立新的一类。举例说，问卷中有这样一个问题：“你认为人生最大的乐趣是什么？”

答案有：A.事业上有成就。

　　　　B.美满的婚姻。

　　　　C.有丰富的经历，见多识广。

如果其中有人选择的答案不止一个，同时选择了A和B；A和C或B和C，这时应增加为六种：

A.事业上有成就。

B.美满的婚姻。

C.有丰富的经历、见多识广。

D.事业上有成就和美满的婚姻。

E.事业上有成就和有丰富的经历、见多识广。

F.美满的婚姻和有丰富的经历、见多识广。

只有这样做的结果，才能保证每一个回答者只能被统计到其中的一类，从而满足了变量互斥性的要求了。

检验统计表是否正确可根据统计表中的百分比总和来判断。如果百分比总和少于100%，表示有的个案情况未能包括在统计表里，即变量取值不满足完备性；反之，如果百分比总和大于100%，则必有些个案情况被同时统计在不止一类，即变量取值不满足互斥性。因此只有百分比总和等于100%时才能表示统计表中变量取值的分类是正确的。但在实际计算中，由于“四舍五入”的缘故，百分比总和有时是100.1%或99.9%等，这些都不算是错误。

统计表可分为不同的类型，例如按其用途分为：调查表，调查所用表格；资料整理表，用于统计资料的整理汇总；分析表，统计分析中所用的一切表格。按其形式分为：简单表，指未加分组的表；分组表，指按一定标准分组所形成的统计表，又分简单分组表和组距分组表；复合表，指通过复合分组所形成的统计表。

统计表的设计原则是科学、实用、简明、美观。具体设计要求是：在形式上，统计表通常应设计为长方形，长宽比例适当；在内容上，统计表的标题应简练明确，且与内容相符，表中内容应完整准确，不留空白，必要时对有关事项做出注解。

下面根据变量的层次，讨论统计表制作上的特点：

(1)定类变量统计表

下面表11－1、表11－2是定类变量的统计表。为了叙述的方便，不妨假定以下是2130户家庭的统计结果。

表11－1　家庭结构的频次分布(＊＊＊地区，1985年，6月份)

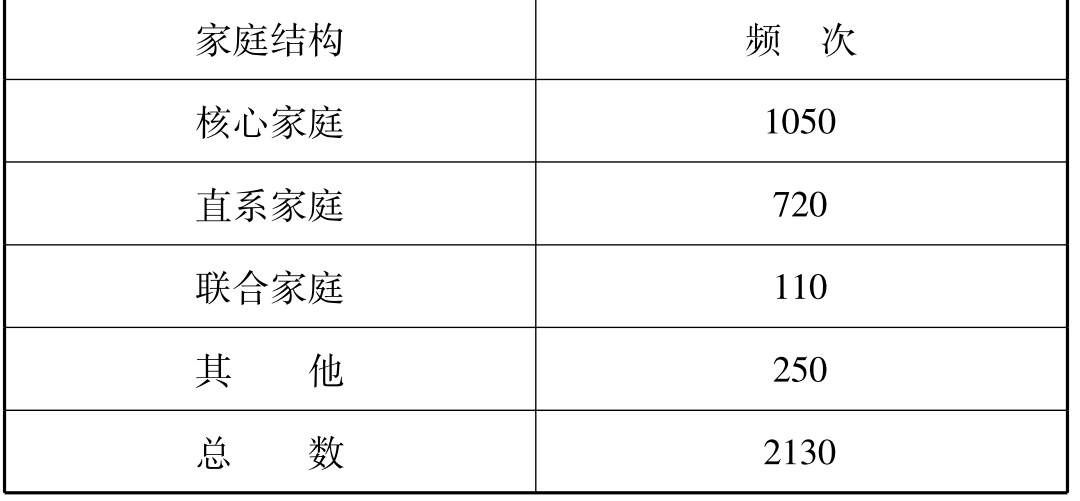
表11－2　家庭结构的百分比分布

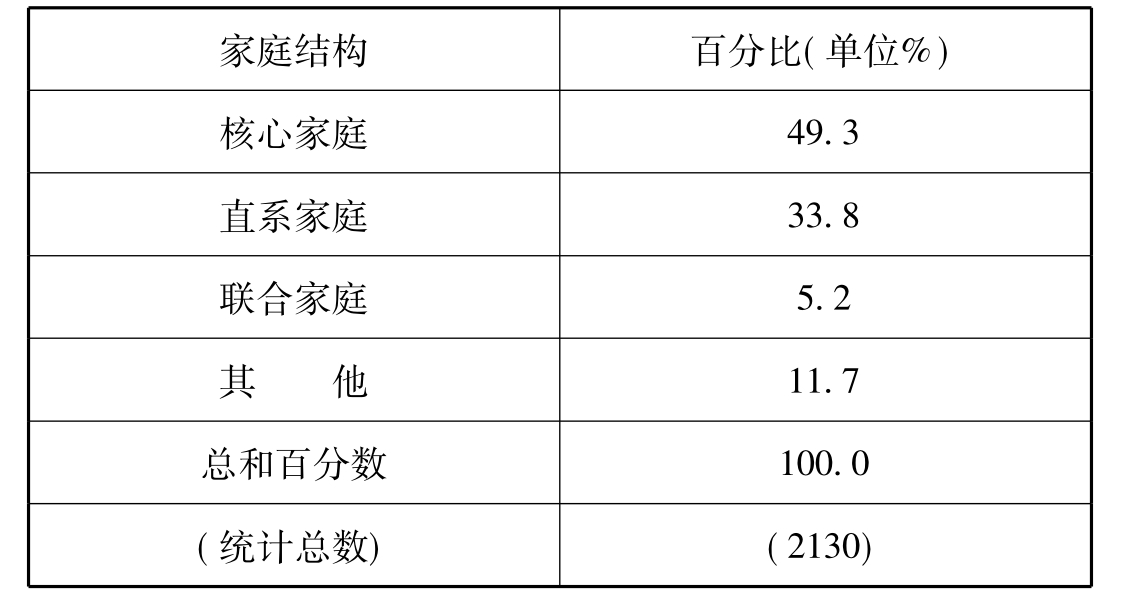
结论：上面两种统计表(表11－1和表11－2)，实际上是等价的。因为通过频次就可换算为百分数，反之亦然。因此，在实际报表中，有一种就够了。但要注意在百分比统计表(表11－2)中，最后一定要注明统计总数。这不仅是为了能够还原为频次表，而且，如果是抽样调查的话，还存在检验上的意义。

(2)定序变量统计表

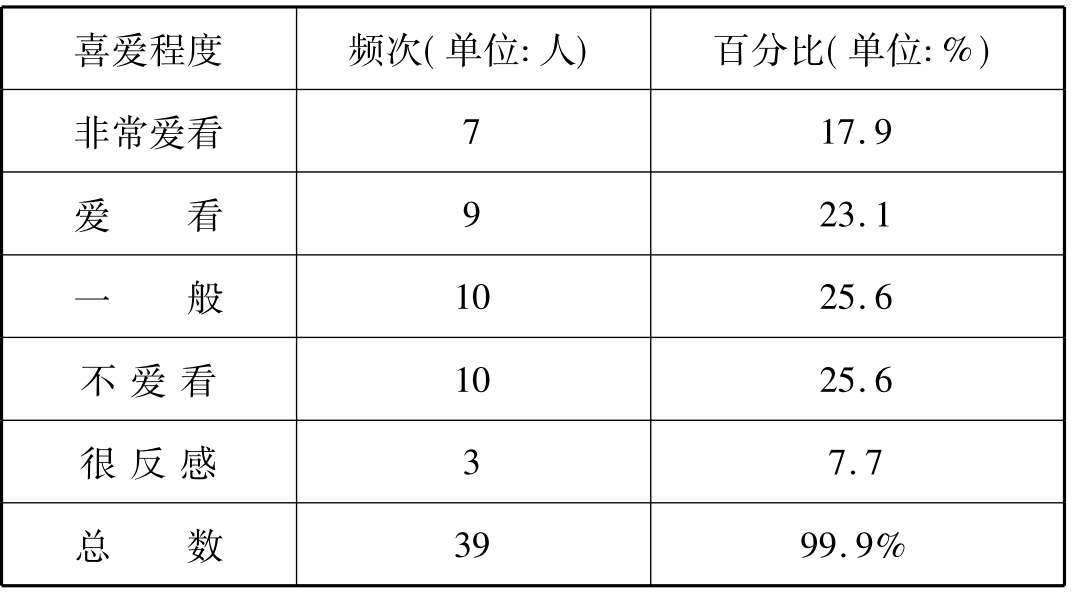
定序变量统计表内容、制作方法与定类变量相同。所不同的是，由于定序变量的取值有大小次序之分，因此在统计表制作时，应保留其变化趋势，不要任意打乱。例如某电影厂为了了解群众对武打片是否爱看，将喜爱程度分为五等：非常爱看；爱看；一般；不爱看；很反感。因此在统计表中，变量取值的排列也应保持以上的次序(表11－3)：

表11－3　××电影院对“武打片”的反映统计

(3)定距变量统计表

对于定距变量，我们要区分它是连续型定距变量，还是离散型定距变量。例如，家庭子女数就是离散型定距变量。它只能取正整数。离散型定距变量的制表方法与定序变量的制表方法相同。统计表中的变量数值，按取值的大小排列，不要任意打乱。

对于连续型变量，由于任意两变量之间的取值那是无穷的，而且，原则上来讲，也没有任意两个观察值是绝对相等的，因此，我们无法简单的运用上述的分布，使每一个取值对应一个确定的频次或百分比。解决的办法是将变量值分为苦干个区间或组，然后统计每一个组内的频次或百分数。例如婚龄问题，由于自成年以后，可在任何一个年龄结婚，因此婚龄是一个连续型定距变量。为了研究婚龄的分布就要将婚龄分组。但组分多少合适呢？是按15～20岁；21～25岁……分呢？还是一岁一分组呢？或者是全部按等距分组呢？还是人数集中的地方分得细一些，人数少的地方分得粗一些，即非等距的分组法分呢？在实际中要考虑如下几个问题：

第一，组数：组数太少会掩盖变量变动时频次的变化。极端的情况下，如果只分一个组，那就什么变化也看不出来了。但组数太多，又会使每组内频次过少，增加偶然因素，使各组高度参差不齐，看不出明显的规律。一般调查总数N与分组数K有如下经验性关系(表11－4)：

表11－4

第二，等距分组与非等距分组：一般来说都是采用等距分组。如人口学中一般以5年作为一档，这样20档正好代表人的寿命为1～100岁。但在社会学中，并非全是等距分组更能反映现象本质的。例如，收入为月薪500元或1000元的职工，他们的生活水平差距是显著的，但月薪为5000元和5500元之间，其差距就小得多，而且这样的人数也少，因此，在分组时，应将低收入分得细一些，高收入分得粗一些，这种非等距分组更能反映现象的本质。

第三，如何决定分组点的精度：前面我们谈到，年龄的分组可采用1～5岁； 6～10岁等。这是统计年龄的精度以年为标准的。如果统计的精度提高，例如统计到月，那么，5岁半的儿童是分到第一组呢，还是分到第二组呢？可见，随着精度的提高，分组点的精度也要提高。一般分组点比原统计资料的精度要高一位。如统计资料的精度为整数，则分组点就取小数点后面的一位计算。举例说，原统计资料的年龄以年计算，统计范围为1～8岁，按2岁一个分组，即有：1～2岁；3～4岁；5～6岁；7～8岁4个分组。为此，应在上述分组值±0.5岁，得：0.5～2.5岁；2.5～4.5岁；4.5～6.5岁；6.5～8.5岁。前者称标明组界，后者称真实组界，试比较上述资料两种组界定义的不同(表11－5)：

表11－5

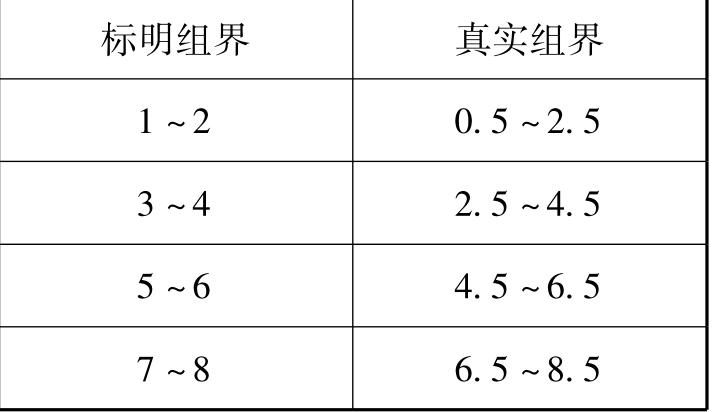
可见，其实组界值是相邻两组标明组界值的中点，它的精度比标明组界要高一位，组与组的分界是连续的，而标明组界则是离散的。标明组界只是分组资料的简化表示，而在实际运算时，都要用到真实组界。下面通过一个实例，来看分组统计表是如何制作的。

图11－1

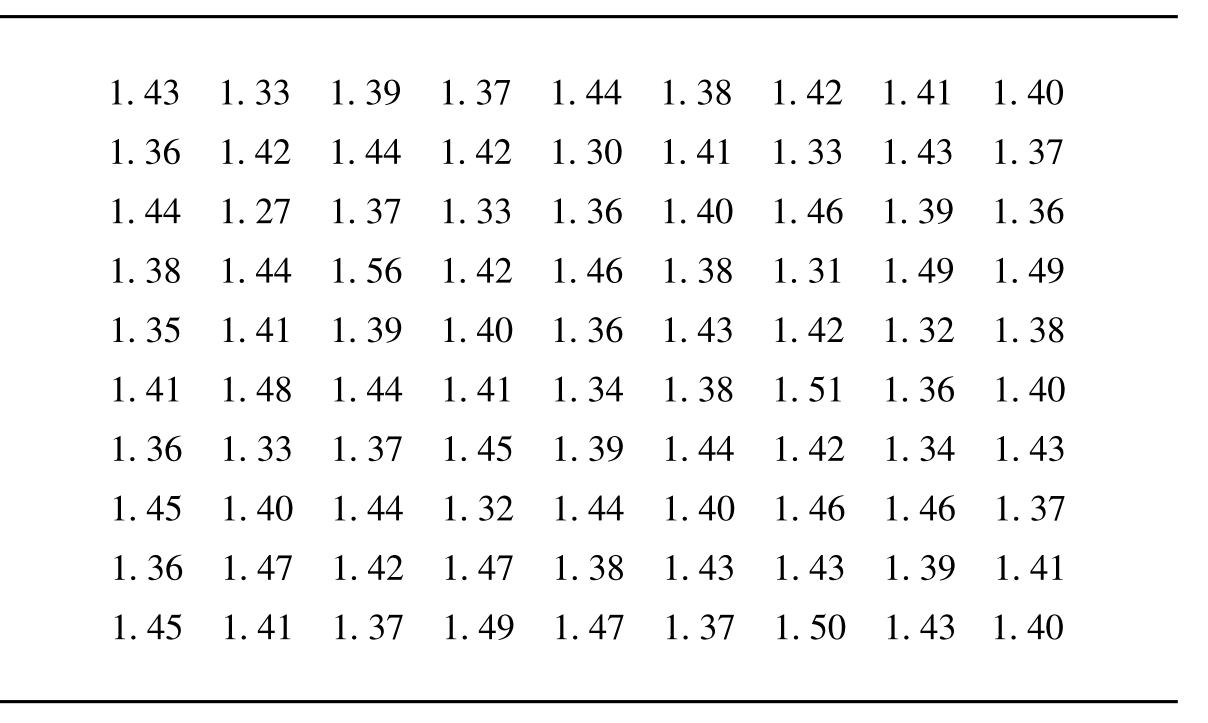
图11－1是100个同龄儿童的身高统计，试作统计表。

步骤1，收集数据，写成10×10数据表(图11－1)，数据总数N=100(数据单位“米”)。

步骤2，找出(图11－1)数据中最大值L，最小值S和极差R。

先在数据表内找出各列的最大值(▲)和最小值(x)，然后找出全体数据的最大值L和最小值S。数据极差R等于最大值L和最小值S之差。

R=L－S=1.56－1.27=0.29

步骤3，把数据分组。根据(图11－1)取分组数K=10

步骤4，计算组距H

H=R÷K=(L－S)÷K=0.29÷10=0.029≈0.03

步骤5，根据组距h和分点精度比原统计数据精度高一位的原则，将数据分为如下10组：

1.265～1.295；1.295～1.325；1.325～1.355；…1.535～1.565；(www.xing528.com)

步骤6，计算各组的中心值bi

中心值是每组中间的数值，可按下式计算：

b=第i组真实下界值+第i组真实上界值

i

2

于是各组的中心值有：

1.28；1.31；1.34；1.37；1.40；1.43；1.46；1.49；1.52；1.55；

步骤7，作频次分布表，即统计表(表11－6)。

根据(图10－1)用唱票的办法画“正”字，进行频次统计，每组的数目，称作

频次。频次与统计总数之比称作相对频次，如再乘100，就是百分数。

表11－6

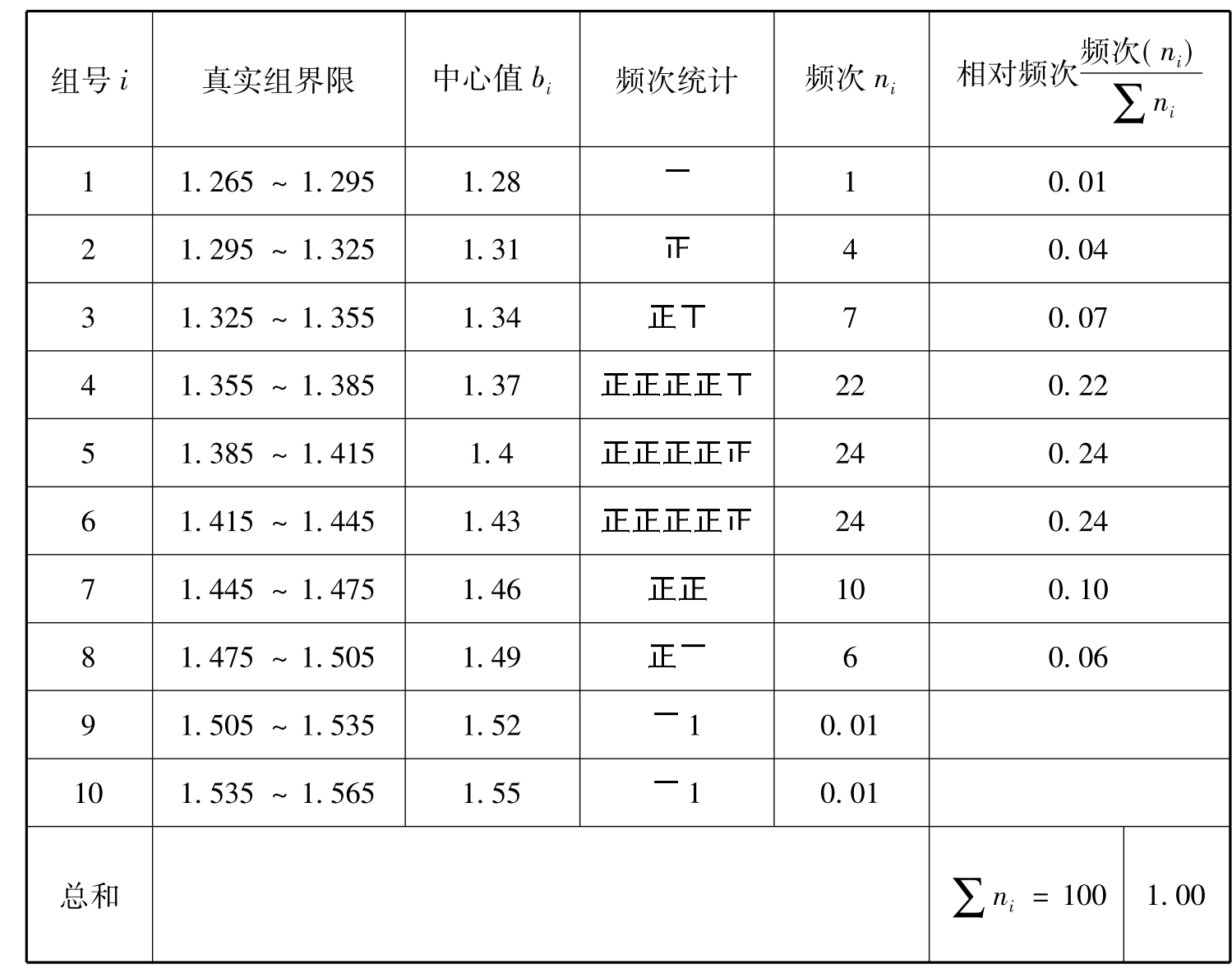
最后一行中频次总和∑n_i应等于调查总数N=∑n_i，如果不等则表示统计过程中有错。

3.统计图

统计图就是用图形的形式来表示变量的分布，所以，又称分布图。它和统计表一样，也不需要文字叙述，就能反映出资料的特性以及资料之间的关系。同时还具有比统计表更为直观与形象的特点。但缺点是不及统计表精确。

根据变量的层次，可选择以下不同的统计图形：

定类变量：圆瓣图，条形图。

定序变量；条形图。

定距变量：直方图，折线图。

(1)圆瓣图

圆瓣图是将资料展示在一个圆平面上，通常用圆形代表现象的总体，用圆瓣代表现象中一种情况，其大小代表变量取值在总体中所占的百分数。

圆瓣图的制作方法是将统计表中的百分数乘以360°，即可得各圆瓣之圆心角度数。现以表11－7为例，说明如何绘制圆瓣图(图11－2)：

表11－7

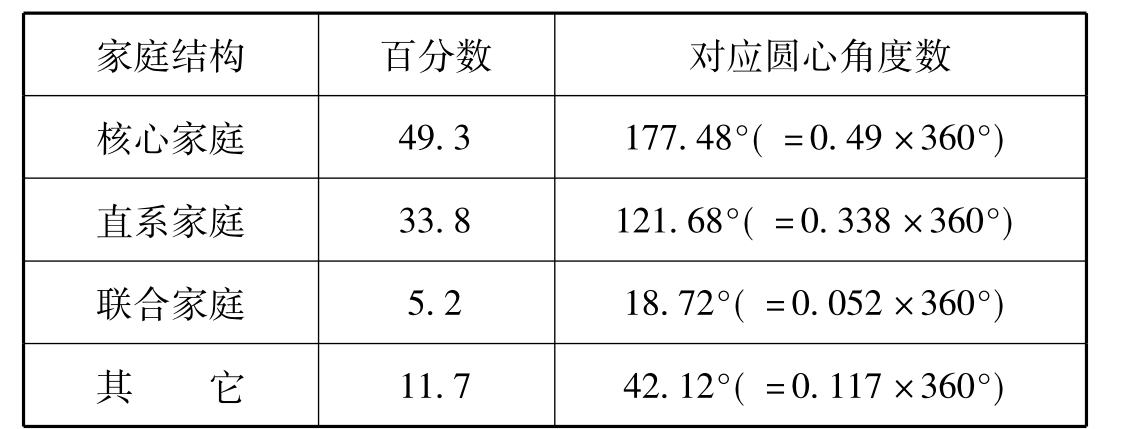
图11－2　家庭结构分布图

由于圆瓣图只表示变量取值在总体中所占的比例，而对变量取值的排列没有要求，因此圆瓣图多用于定类变量。

(2)条形图

条形图又称柱形图，是用长条的高度来表示资料类别的次数或百分数。而长条的宽度没有意义，一般都画成等宽长条。长条既可画成平行于横轴，也可画成平行于纵轴。如果是定类变量，图形画作离散的长条；如果是定序变量，则长条的排列次序应与变量取值的次序相一致，且图形可画作紧挨着的长条或离散的长条。

定类变量：长条排列次序可以任意，条形是离散的(图11－3)：

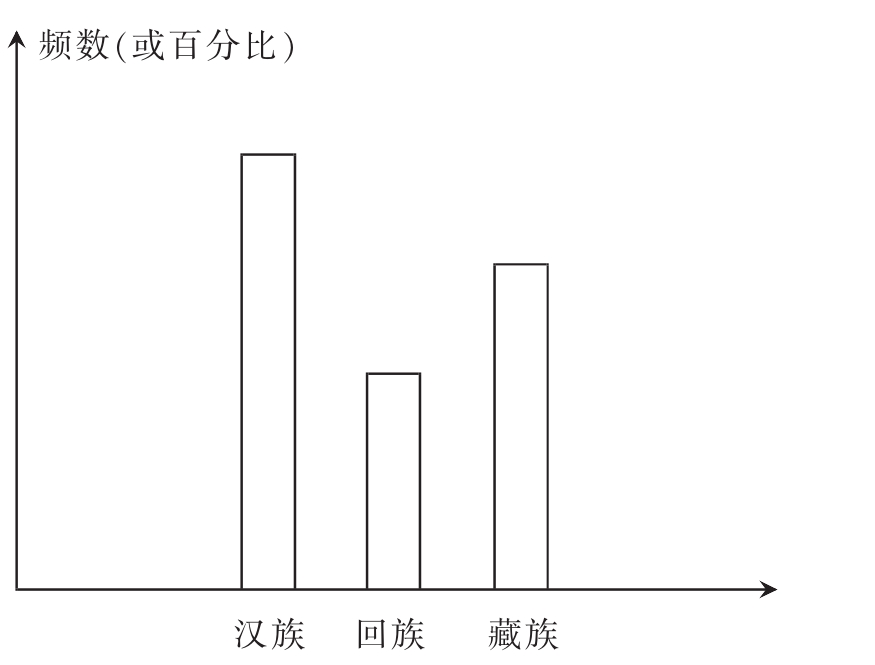
图11－3

定序变量：长条按序排列，条形可以是紧挨着的(图11－4)，也可以是离散的(图11－5)。

图11－4

图11－5

(3)直方图

直方图从图形来看，也是由紧挨着的长条所组成(图11－4)，但它与条形图不同，直方图的宽度是有意义的。一般说，直方图是以长条的面积(长与宽的乘积)来表示频次或相对频次。而条形的长度，即纵轴高度表示的是频次密度(单位组距所含有的频次)或相对频次密度。

直方图仅适用于定距变量。用密度作为条形高度的原因，在于连续型定距变量可采用非等距分组的缘故。对于等距分组，用频次或密度作为条形高度，图形的相对比例关系是不变的，因此，仍可用频次(或称频数)作为条形的相对高度。但在非等距分组情况下，如果用频次作为条形高度，将会产生错误。举例说，婚龄统计表中有如下两组数据：

表11－8

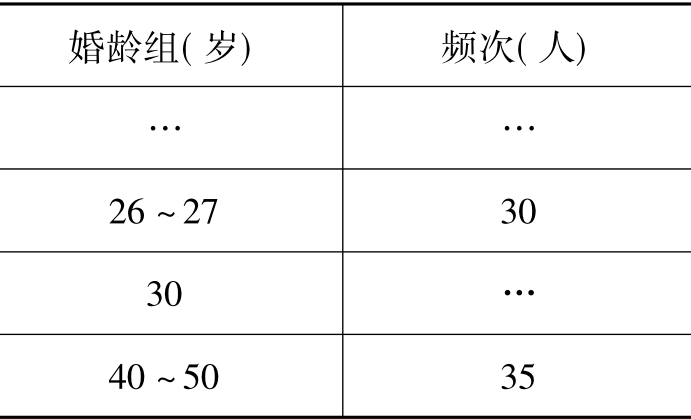
如果根据频次来比较，就会得出40～50岁结婚的人比26～27岁结婚的人还多，显然这是错误的。正确的方法，应该根据频次密度来比较和画直方图。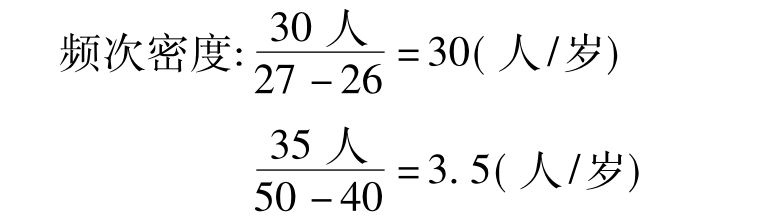

可见，在26～27岁结婚的频次密度远比40～50岁之间的频次密度更高。

下面是根据(图11－1)所作有关100个儿童同龄人身高的频数分布直方图(图10－6)。

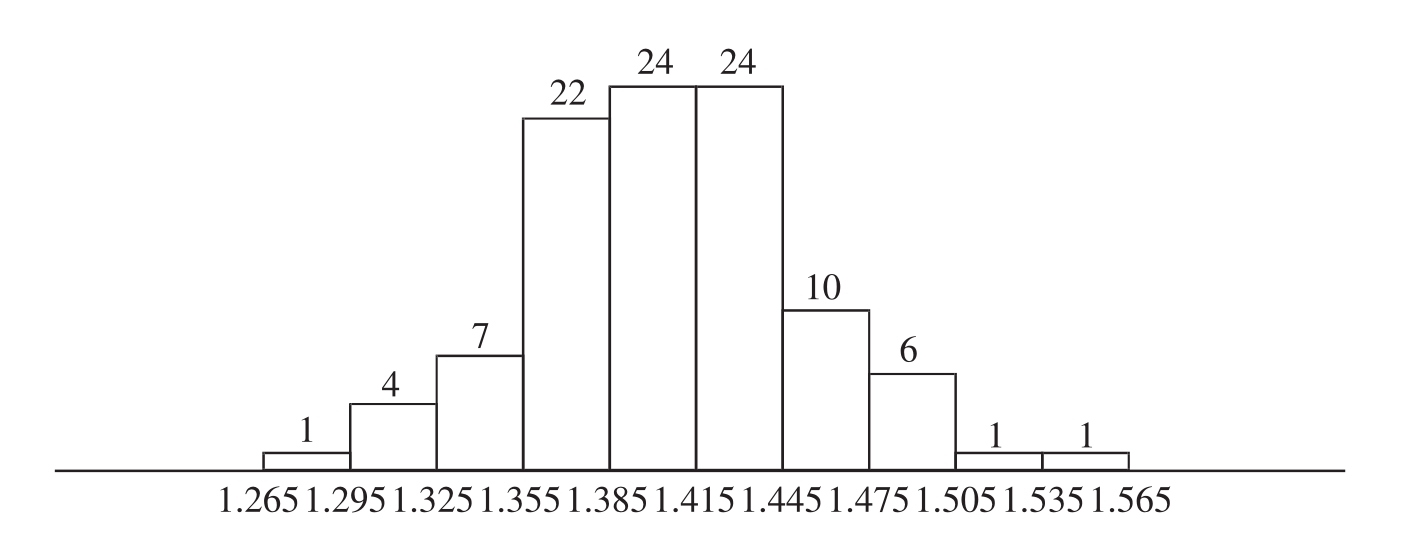
图11－6

根据直方图(图11－6)，可以清晰看出，所统计的同龄儿童，身高基本集中在1.355～1.455m，太高和太矮的儿童都比较少见。

(4)折线图

如果用直线连接直方图中条形顶端的中点，就得折线图。折线图可使资料频次分布的趋势更一目了然。

对于离散型定距变量，将变量值、频数对(x_i，n_i)的集合(频次分布)根据坐标连成的图就是折线图。见(图11－7)：

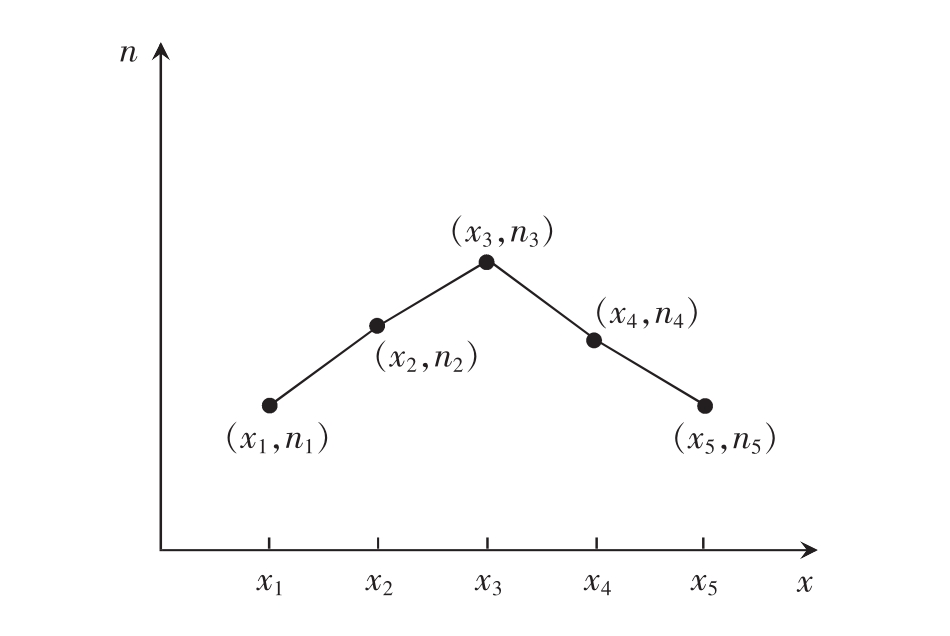
图11－7

对于连续型定距变量，用组中心值bi代替变量值，并用该组相应的频次作为bi的频次，于是(bi，ni)坐标的连线就是折线图(见图11－7)。

当组距逐渐减小时，折线将逐渐平滑为曲线。

4.图和表的累计表示

统计图和统计表告诉我们的是某一个变量值(或某一组)所对应的频次是多少。但有时我们不仅需要了解频次分布，还需要了解小于某一变量值或大于某一变量值总共的频次是多少，这时就要用到图和表的累计表示。所谓累计图或累计表表示的是大于某个变量值的频次是多少或小于某个变量值的频次是多少。

下面通过例子来比较统计图、表和累计图、表。

(表11－9和图11－8)表示的是12户家庭子女数的统计表和统计图：

表11－9

续表：

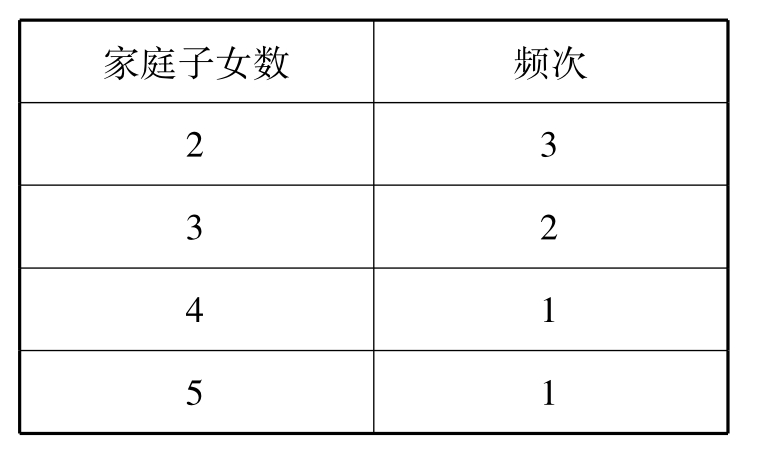
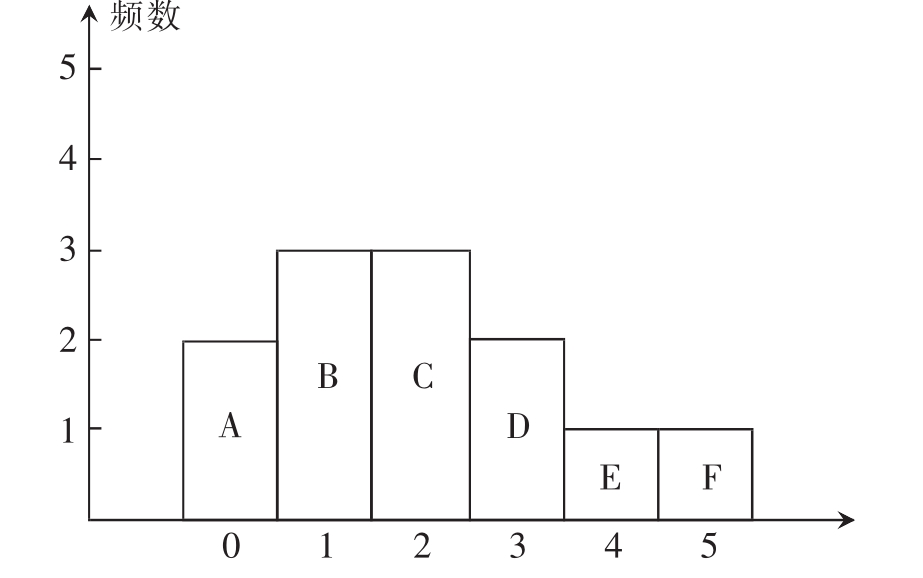
图11－8

现在用cf↑表示小于某一个子女数的累计频数，cf↓表示大于某一个于女数的累计频数。

表11－10

同理，如果把频次换成频率，还可以作成累计频率c%↑或c%↓分布图。