循环经济影响因素研究及实现路径-检验与描述统计

一、检验

本研究使用AMOS 7.0版本软件进行可持续发展与循环经济之间的路径分析，运用Lisrel8.70版本软件进行验证性因子分析，具体统计结果如下。

（一）描述性统计

本书主要用最低分值、最高分值、均值和标准差来对问卷结果进行描述统计。描述统计采用SPSS统计软件进行分析，分析结果如表6－10所示。

表6－10　　　　　　量表描述性统计

（二）验证性因子分析

结构方程模型（Structural Equation Modeling，SEM），也有人称之为协方差结构模型（Covariance Structure Models，CSM），或线性结构模型（Linear Structural Relations Models，LISREL）。它用于对复杂现象的模式进行处理，根据理论模式与实际数据关系的一致性程度，对理论模式作出评价，从而达到对复杂的实际问题进行定量研究，找出其规律性的目的。在研究中，把描述研究对象特征的指标或现象称为变量，对无法直接测量的变量称为潜变量（Latent Variable）或隐变量，可直接测量的变量记为观测变量（Manifest Variable）或显变量，结构方程用于研究潜变量与观测变量之间的关系。结构方程模型分为测量模型和结构模型。测量模型描述了观测变量与潜变量之间的关系，结构模型描述了潜变量与可测变量之间的关系。测量模型（Measurement Mode1）又称验证性因子模型，结构模型（Structural Equation Model）又称潜变量模型（Latent Variable Model）。结构方程模型的建立主要有3个步骤:一是构造模型，二是估计结构模型参数，三是检验模型对实际数据的拟合程度。

本研究建构的理论模型中，有4个外因潜在变项，即创新投入、资源开采量、固定资产投入以及环保投资。创新投入这个潜在变量用了8个观察变量；资源开采量这个潜在变量用了5个观察变量；固定资产投入这个潜在变量用了5个观察变量；环保投资这个潜在变量用了3个观察变量。各观察变量都有几个测量条款进行测量。

在进行了验证性因子分析的基础上，为了明晰4个影响因素与可持续发展之间的关系，将4个外因潜变量（4个影响因素）与内因潜变量（可持续发展）之间的关系量化，我们采用二阶因子分析的方法来测算。

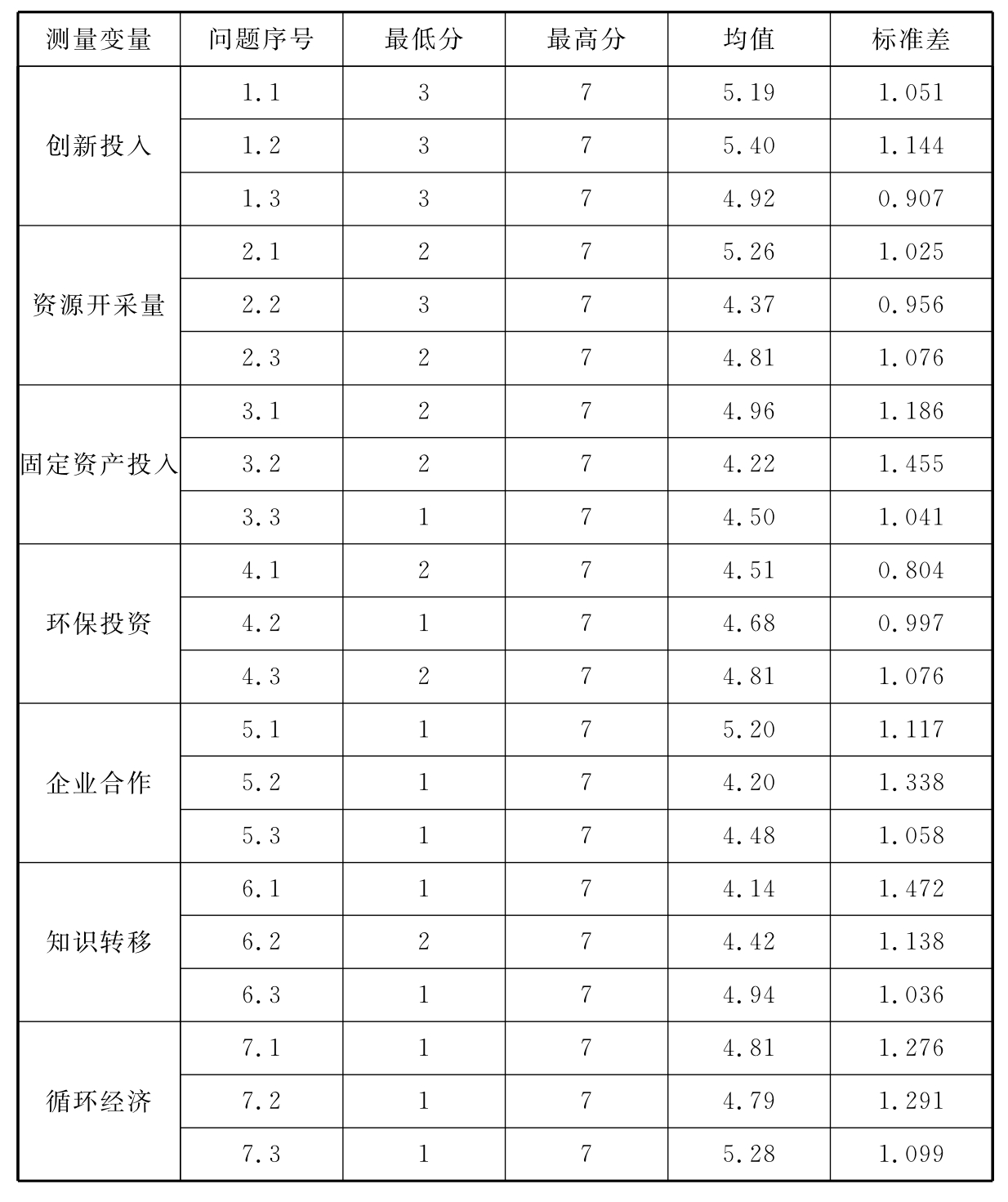
经由Lisrel8.70版本估计（图6－1），Minimum Fit FunctionChi－Square＝285.70，P＝0.00，没有达到显著性水平，表示本研究假设模式之共变量矩阵与实证资料之共变量矩阵之间差异并不显著。从绝对适配量测来看，RMSEA＝0.058，接近于0.05，显示本研究假设模式可以接受；ECVI＝3.30，小于独立模式的ECVI值，接近于饱和模式ECVI值，也显示假设模式是可以接受的；从增值适配量测来看，NFI＝0.92，大于接受值0.9，也显示假设模式可以接受；CFI＝0.97，高于接受值0.9，显示模式在可以接受的边缘。整体而言，大部分绝对适配量测、增值适配量测、简效适配量测皆通过要求的接受值，显示本假设模式可以接受。这显示本假设模式是一个相当符合实证资料的模式。本研究运用更加成熟的统计软件Lisre18.70检验模型的合适性，结果表明，设计的研究模型是稳定的、合适的。

图6－1　验证性因子分析拟合结果输出图

好的结构模型能既简单又准确地反映变量之间的关系。因此，对可持续发展的内涵构成抽取二级因子，模型的自由度是185（df），根均方差（RMSEA）是0.058，非标准拟合指数（NNFI）是0.96，比较拟合指数（CFI）是0.97，可以看出模型拟合较好，表明影响可持续发展的4个关键因素可以解释可持续发展这一变量（图6－2）。

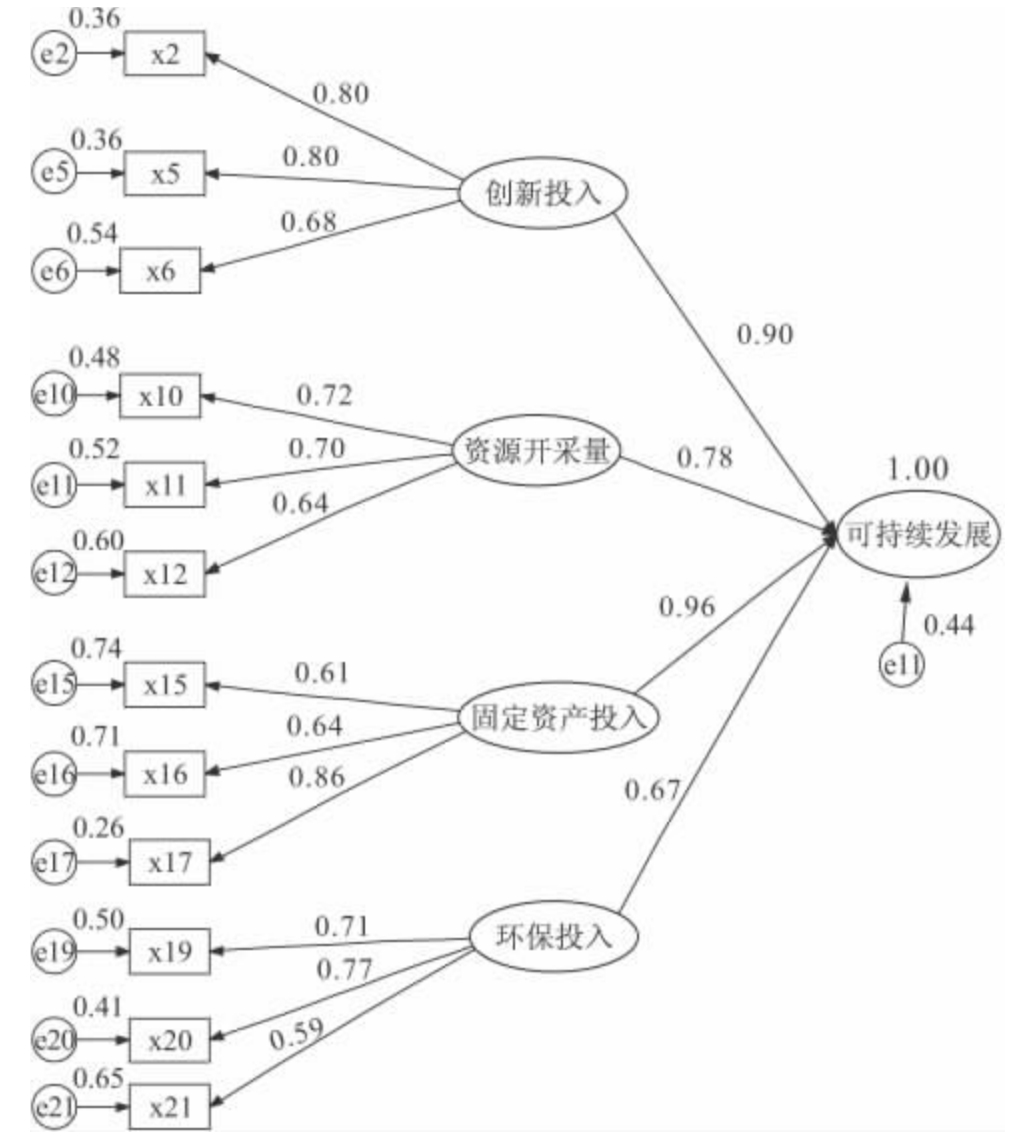
图6－2　可持续发展关键影响因素验证性因子分析模型计算结果

（三）路径分析

本研究拟采用路径分析（Path Analysis）的方法对研究假设进行验证。路径分析要求任意两个变量之间的路径系数必须达到α＝0.05的显著相关水平，如果未达到则表示两个变量之间因果关系较弱，不能采取该路径。在这种情况下必须探寻新的路径重新分析，并藉由此获取模型中各独立变量对因变量的影响程度。

路径分析的方法由遗传学家S Wright于1921年首次提出，此种方法在社会学、心理学、管理学、教育学等行为学科中被广泛运用。路径分析的前提条件在于其是在一种封闭系统中，对变量之间因果或非因果线性关系的分析方法。本质来说，路径分析不能推测变量之间的因果关系，其仅具有回溯功能，来验证理论假设模型的可靠程度。路径分析的运用具体建立在以下假设之上:

（1）变量之间的因果关系是提前定好的，且为单项作用，不考虑变量之间的互动关系及反馈关系；

（2）变量之间的关系为线性关系并可被叠加；

（3）变量的内生残差项相互独立，不与任一变量或残差项相关；

（4）测量必须建立在一定的信效度基础之上。

根本上，路径分析是运用一组回归方程来判定自变量与因变量之间的路径关系，以及与这种路径需经由中介变量影响的相关程度。在统计学的层面上，路径分析可以被看作为一种特殊的回归方程，但在实际的运用过程中，路径分析强调该方程可被理论假说解释的程度，假设的理论模型须与回归方程之间存在意义上的一致性。所以，路径分析主要在于发现研究数据在理论假设与统计学意义之间的矛盾。

本研究中自变量、因变量及中介变量的设定均符合路径分析的研究假设，可以进行路径分析，本研究模型拟合情况如图6－3所示。

从表6－11～表6－13显示的结果可知，4个外因变量及3个误差变量的方差参数估计均达到了0.05的显著水平，表示上述9个变量的方差在总体中均显著不等于0，残差项的方差也均为正数，没有出现负的误差变异，表示模型界定有效，数据文件没有错误。

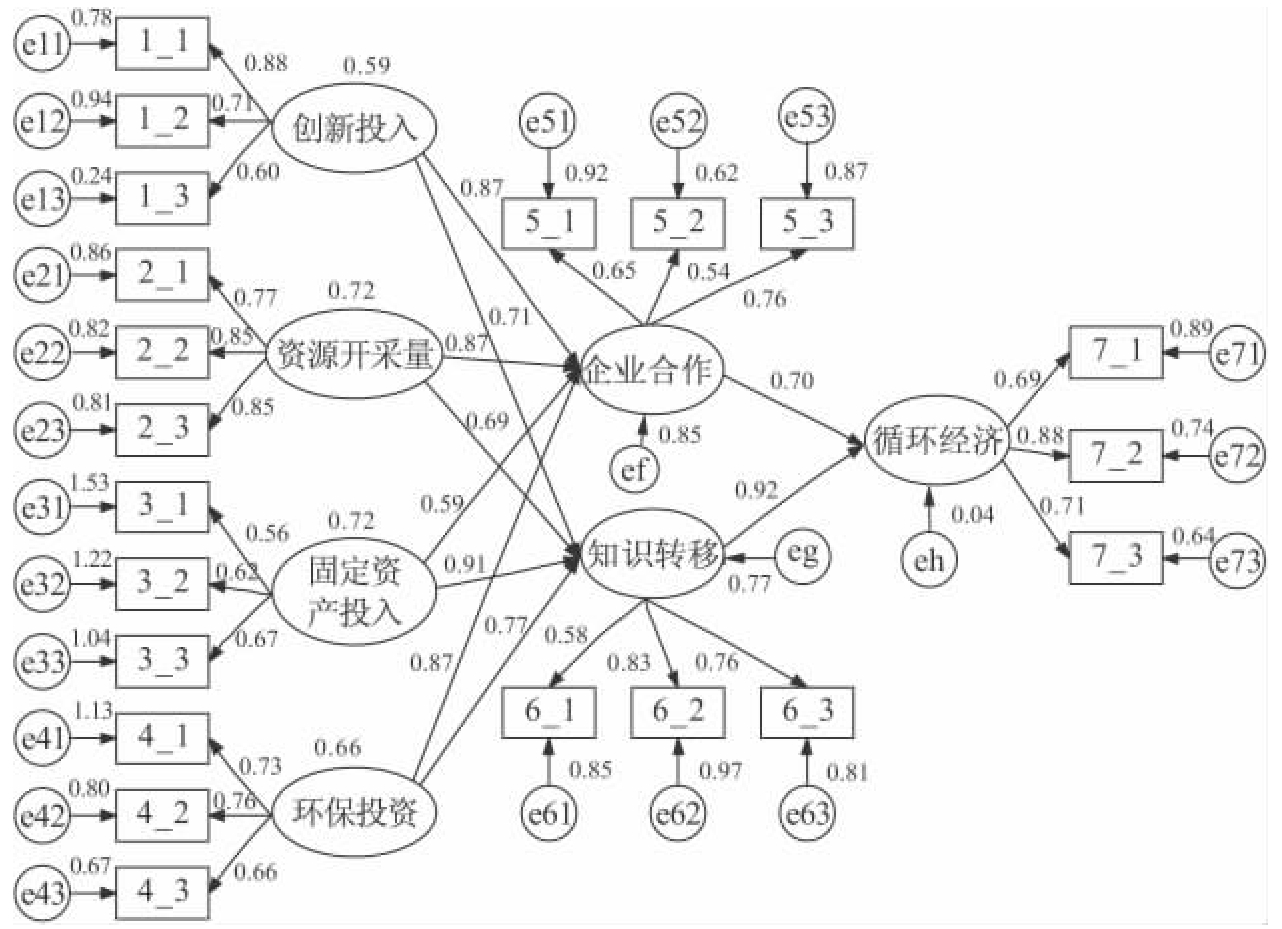
图6－3　可持续发展对循环经济影响路径图

表6－11　　　　　　回归加权值Regression Weights

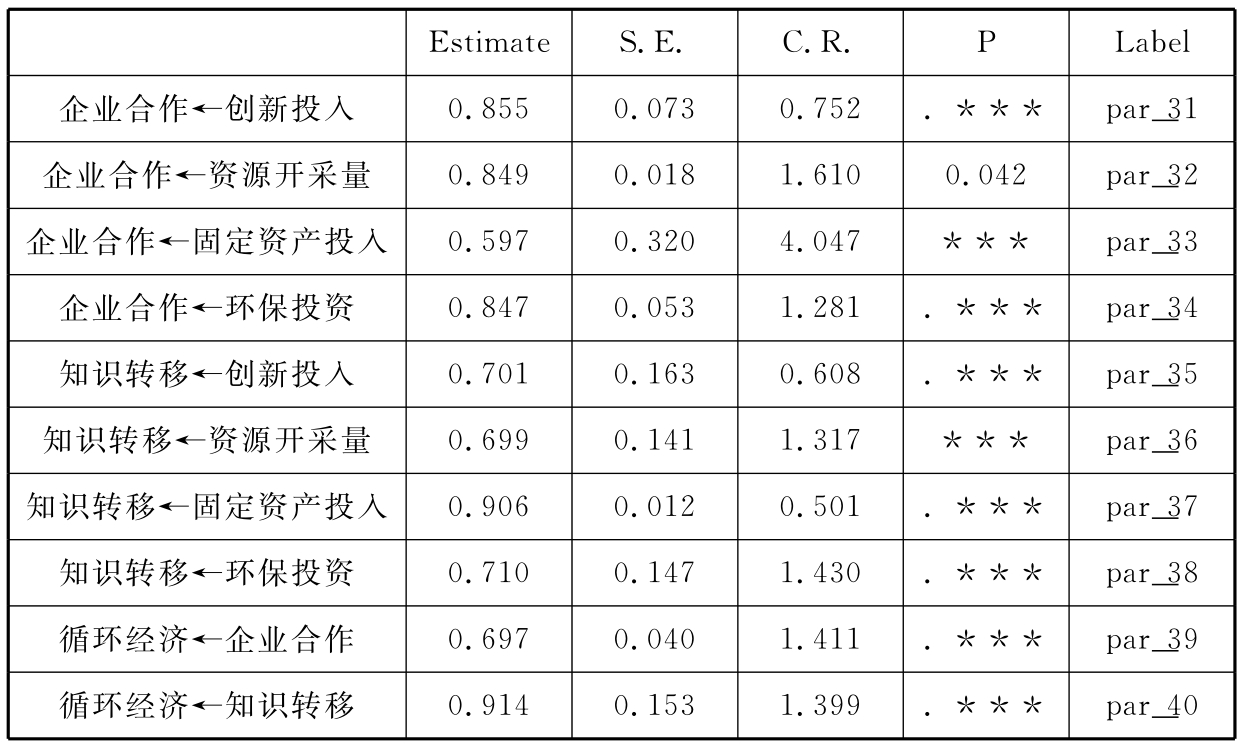
表6－12　　　　　　标准化回归系数Standardized Regression Weights

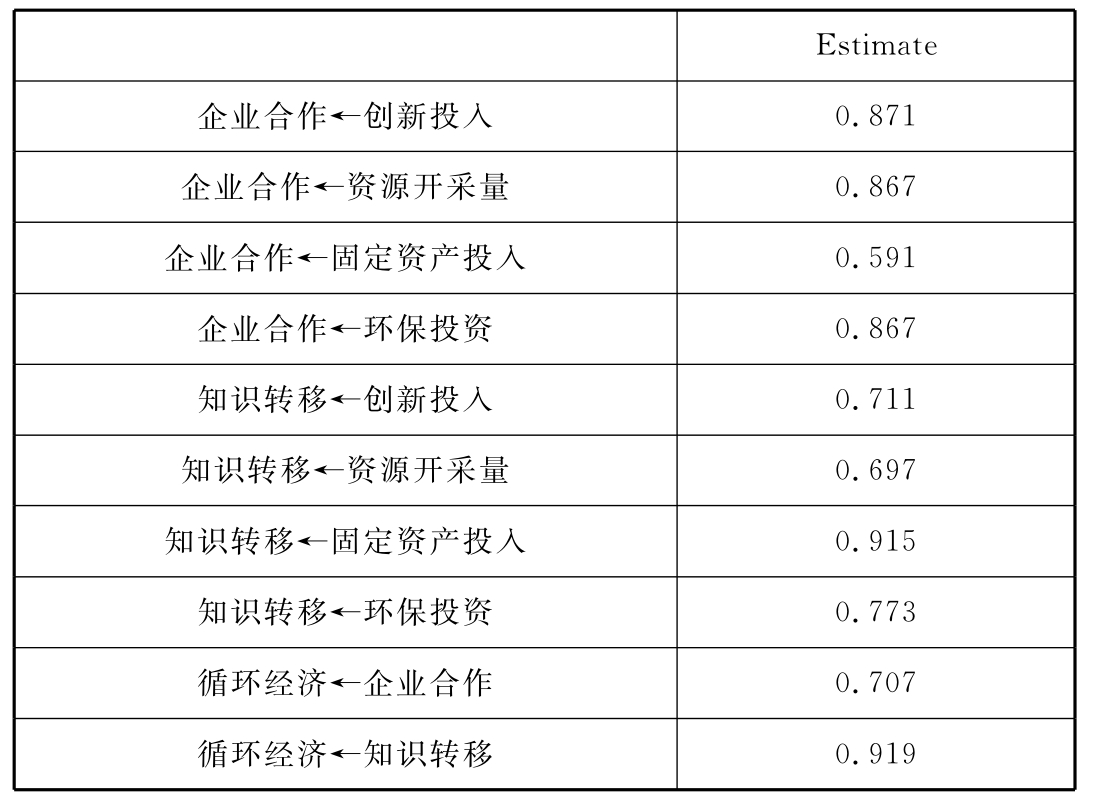
表6－13　　　　　　方差参数估计Variances

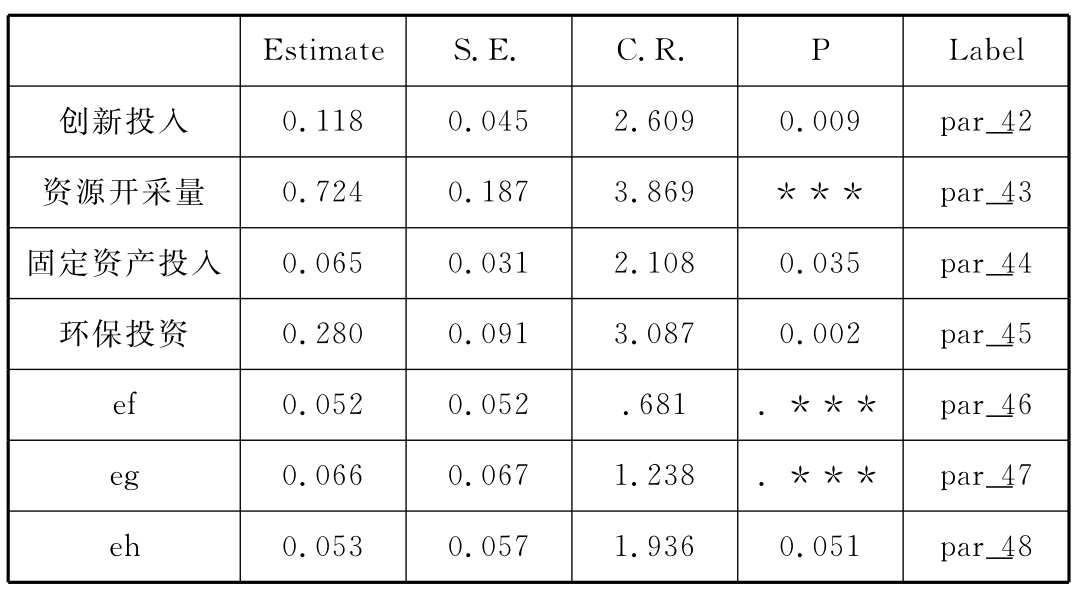
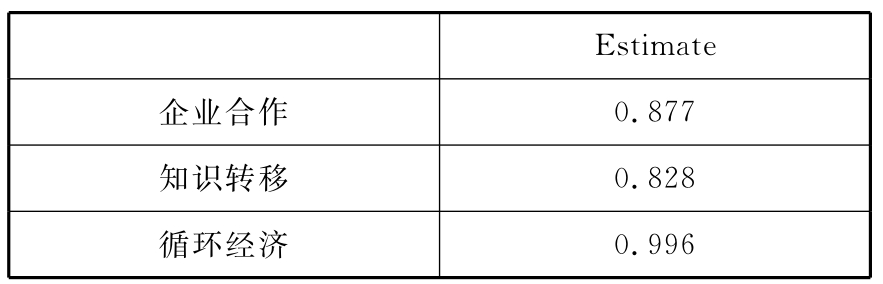
中介变量“企业合作”被外因变量“创新投入”、“资源开采量”、“固定资产投入”、“环保投资”解释的变异量为87.7%；“知识转移”被外因变量“创新投入”、“资源开采量”、“固定资产投入”、“环保投资”解释的变异量为82.8%；中介变量“知识转移”和“企业合作”可以解释内因变量“循环经济”99.6%的变异量。

（四）中介效应

中介效应检测的目的在于考察变量之间的影响关系（a，b）不是通过直接的因果关系连接，而是通过一个或者一个以上的变量（m）通过间接的关系相连接。在这种情况下，我们把变量（m）称为中介变量，并将a通过m影响b的间接影响称之为中介效应。中介效应是间接效应的一种，但是彼此不能等同，有两个以上的中介变量时，间接效应等于所有中介效应之和。在本研究中，4个自变量和因变量“循环经济”之间难以直接影响，而在现实的世界中难以测量的变量之间也不容易出现直接的影响，更多时候，变量与变量之间的影响是一种间接的影响。在所有变量都中心化的基础上，中介关系可以用回归方程表示，具体有以下3种方式:

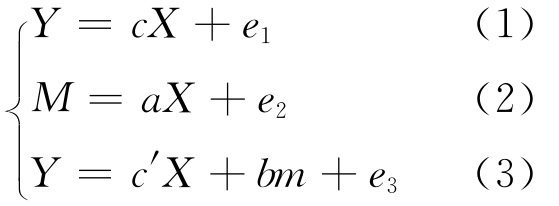
本研究拟采用的中介效应检验的具体方法是依次检验法，顾名思义，就是将以上3个回归方程依次检验。①首先检验式（1），如果c显著则进入式（2），不显著则停止中介效应的检验；②在c通过显著性检验的基础上，检验式（2），若a显著则进入式（3），不显著的话停止中介效应的检验；③在式（3）中，需要注意两个参数，在检验式（3）的基础上，如果b显著，则说明模型中介效应显著，若c′显著的话，就说明模型是不完全中介效应，反之则是完全中介效应。

但以上步骤的中介效应的检验对于较弱的中介效应检验不甚理想，容易出现接受虚无假设即作出中介效应不存在的判断，在此种情况下应当在作依次检验法的同时进行Sobel检验。具体步骤应当如下:①将自变量、中介变量和因变量各题项所对应的潜变量合并取均值并中心化；②检验Y＝cX＋e₁中c是否显著，若显著，继续检验a与b是否显著，进一步判断有无中介效应；③检验式（3）中c′是否显著；④通过c′的显著性判断是完全中介效应还是不完全中介效应，c′显著为不完全中介效应，不显著为完全中介效应。

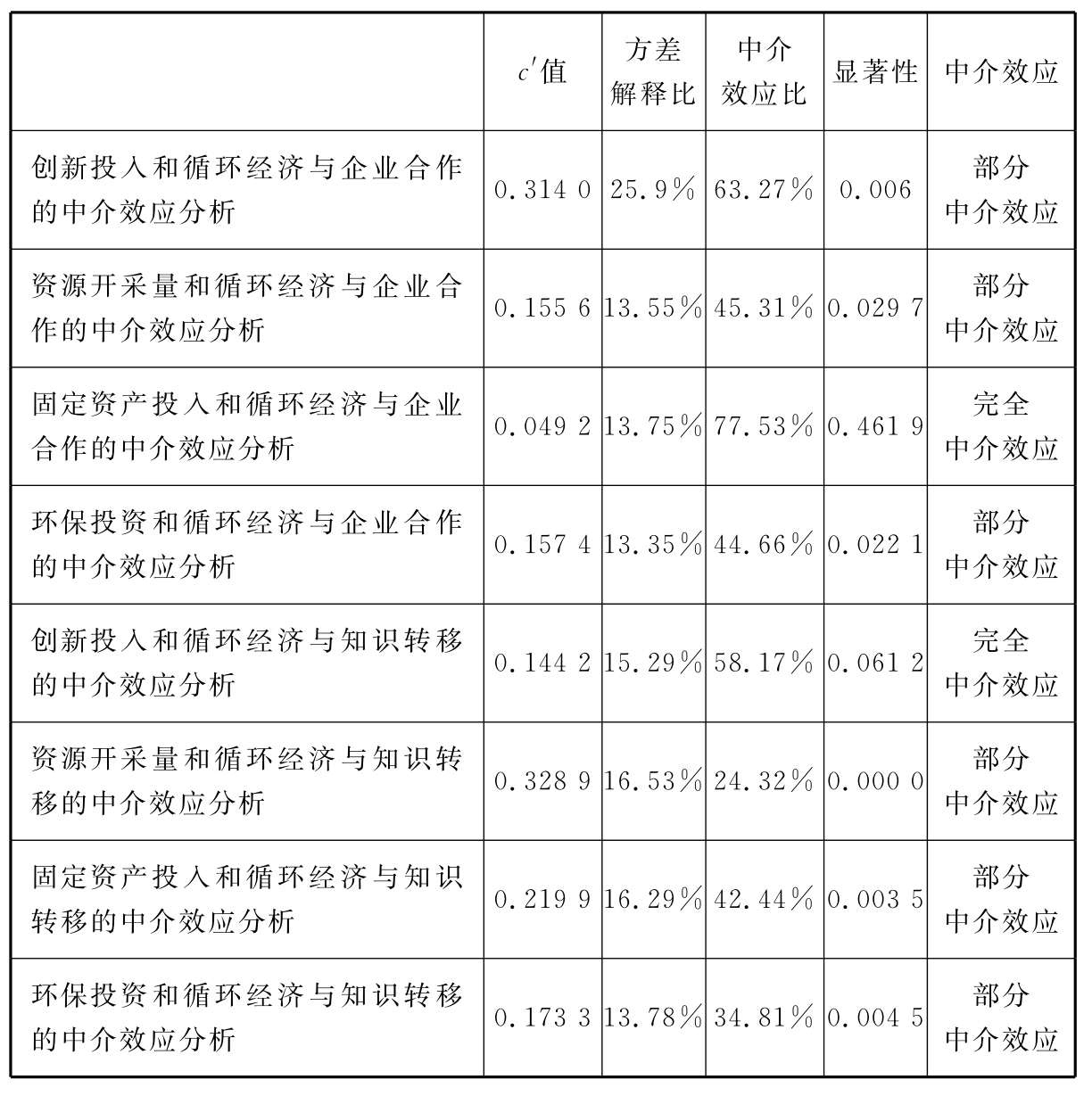
根据以上方程进行计算，表6－14是对本研究中可持续发展与循环经济路径模型中两个中介变量“企业合作”和“知识转移”的中介效应分析。(www.xing528.com)

表6－14　　　　　　Squared Multiple Correlations

首先以“创新投入”和“循环经济”与“企业合作”的中介效应分析为例，进一步说明Sobel检验的方法及步骤。

以下是具体演算结果:

VARIABLES IN SIMPLE MEDIATION MODEL

Y　　　　　循环经济

X　　　　　创新投入

M　　　　　企业合作

DESCRIPTIVES STATISTICS AND PEARSON CORRELATIONS

　　　　　Mean　　　　SD　　　循环经济　创新投入　企业合作

循环经济　4.9816　　0.8957　　1.0000　　0.2594　　0.5720

创新投入　5.0321　　0.7488　　0.2594　　1.0000　　0.3022

企业合作　4.8309　　0.7348　　0.5720　　0.3022　　1.0000

SAMPLE SIZE

　307

DIRECT And TOTAL EFFECTS

　　　　　　　Coeff　　　s.e.　　　　t　　　　Sig（two）

　b（YX）　0.3103　　　0.0779　　　3.9842　　　0.0001

　b（MX）　0.2965　　　0.0631　　　4.7016　　　0.0000

b（YM.X）　0.6622　　　0.0704　　　9.4006　　　0.0000

b（YX.M）　0.3140　　　0.0691　　　1.6487　　　0.0006

INDIRECT EFFECT And SIGNIFICANCE USING　NORMALDISTRIBUTION

　　Value　s.e.LL95CI　UL95CI　Z　Sig（two）　Effect　0.1963　0.0469　0.1044　0.2883　4.1861　0.0000 BOOTSTRAP RESULTS For INDIRECT EFFECT

　　Data　Mean　s.e.　LL95CI　UL95CI　LL99CI　UL99CI　Effect　0.1963　0.1960　0.0583　0.0869　0.3240　0.0664　0.3712NUMBER OF BOOTSTRAP RESAMPLES

　1000

FAIRCHILD ET AL.（2009）VARIANCE IN Y ACCOUNTED FOR BY INDIRECT EFFECT:

　0.2590

由结果可知，总效应、中介效应与间接效应均已达到显著，其中c值为0.3103，a值为0.2965，b值为0.6622，c′值为0.3140，中介效应解释了自变量25.9%的方差，中介效应占总效应比值effect＝ab／c＝0.2965×0.6622／0.3103＝0.6327，由于c′显著，故自变量与因变量之间存在部分中介效应，中介效应占总效应的比值为63.27%。

从表6－15可以看出，中介变量“企业合作”与“知识转移”在可持续发展与循环经济的路径关系中全部存在中介效应。其中“企业合作”在“固定资产投入”与“循环经济”路径之间存在完全中介效应，“知识转移”在“创新投入”与“循环经济”路径之间存在完全中介效应，其余各条路径之中存在不完全中介效应。

（五）模型检验

对于结构方程模型进行检验，主要考察的指标就是各种拟合指数。关于拟合指数的研究一直是学者们关注的焦点，从最早Tucker和Lewis所提出的TLI（Tucker、Lewis，1973）到Marsh和Balla提出的NTLI（Marsh、Balla，1996），在文献上被正式应用过的拟合指数超过40个，于是问题就摆在了我们面前——到底哪些拟合指数可以被认为是有效的？一般说来，从不同的角度出发，会有不同的意见和结论。例如以相对拟合指数和近似误差均方根来说，传统上一般认为相对拟合指数大于0.9而近似误差均方根小于0.08被认为是可接受的，而Bentler的研究表明，对极大似然估计（ML）和广义最小二乘估计（GLS）来说，RMSEA值取小于0.06更为合适（Bentler，1996）。以上两种不同的标准表明了在不同限定条件下对拟合指数的选取差异，虽然后者明显更为苛刻，但极有可能成为未来唯一的标准而被人们更加重视。

表6－15　　　　　　模型中介效应分析

判断一个拟合指数是否足够好，最好的检验方法就是看其受样本容量影响的大小。这是一个很简单的判断方法，在理论上也有着较为清晰的解释:一个易受样本容量影响的拟合指数或者说一个拟合指数会随着样本容量大小的影响而产生系统的变化，那么由这种样本所计算出的指数一般来说是总体的有偏估计，用它来检验模型，很可能会出现这种情况——结论会随着样本容量的大小而变化，这样我们很难知道在何种样本容量下会有较为理想的结论。Marsh曾经使用蒙特卡洛方法（Monte Carlo）对各种真模型与误设模型进行了检验，讨论了超过30个较流行的拟合指数和样本容量之间的关系，发现仅有TLI不受样本容量大小的影响（Marsh，1996）。

指数TLI（非正态化拟合指数）一般被认为是最关键的检验拟合指数之一，但是其缺陷在于取值范围过大（0～1），这就会使人认为不宜判断出两种存有微小偏差的预设模型之间的差异。其余拟合指数出现的出发点都在于对TLI不满足的情况下，NFI（标准拟合指数被认为是更加可靠的）就是其中之一。Bentler和Bonett提出了一个0.9的准则，认为NFI的指数范围在0.9～1之间是普遍被接受拟合程度较好的，而在这个范围之外则是不好的拟合（Bentler、Bonett，1980）。比较拟合指数（CFI）同样不宜受到样本容量的影响，Bentler认为在基于小样本的模型估计中，CFI比其他的指数的标准差都要小，所以是一个可靠的拟合指数（Bentler，1992）。另外，近似误差均方根（RMSEA）也是检验结构方程模型中重要的拟合指数，近似误差均方根由Steiger与Lind于1980年提出。近似误差均方根的本质在于将离中指数（NCP）重新标度后得到的DK规范化后得到PDF，其与自由度的比值就是RMSEA（近似误差均方根）（Steiger、Lind，1980）。RMSEA的优点在于其受到样本容量的影响不大，对只有少量参数的误设模型具有一定的敏感性，其取值范围一般认为低于0.1是可以接受的，低于0.05是较好的拟合（Steiger、Lind，1980）。

以上讨论的拟合指数都是检验结构方程模型的重要标准，对于本研究所提出的模型应当基于以上指数进行进一步的检验，模型总体拟合检验见表6－16。

表6－16　　　　　　模型总体拟合检验

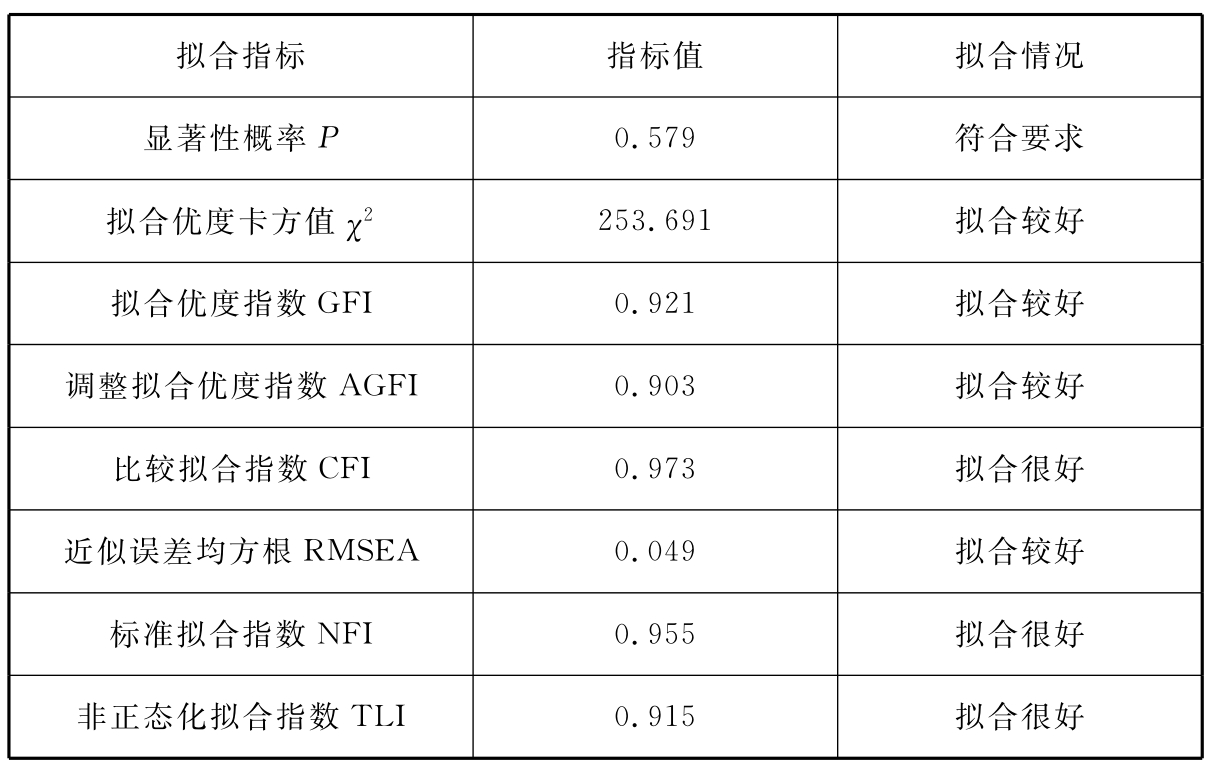
由表6－16可知，整体模型适配度检验的卡方值在自由度等于127的情况下是253.691，显著性概率为P＝0.579＞0.05，未达到0.05显著水平，接受虚无假设，表示修正过的理论模型可以与样本数据适配。再由CMIN／DF（卡方与自由度比值）＝251.492＞2.000，RMSEA＝0.049＜1，GFI＝0.921＞0.9，NFI＝0.955＞0.9，AGFI＝0.903＞0.9，RFI＝0.964＞0.9，IFI≥0.9，TLI＝0.915＞0.9，CFI＝0.973＞0.9，均达到标准，FMIN＝0.001，接近于0。预设模型的其他指标均低于独立模型的数值，表示整体模型适配度良好，经过修正的理论模型与实际数据可以适配。