循环经济试验带来技术效率提升：研究成果及讨论

第三节　结果及讨论

将作为样本的企业的“技术创新投入”、“环境保护投入”、“企业间合作频度”、“营业收入”4项指标分别代入预设模型中，将2001—2010年间的每项指标作为决策变量，用DEA Solver软件进行计算，得到如下结果，具体详见表5－1。

表5－1　　　　　　C²R模型求解结果

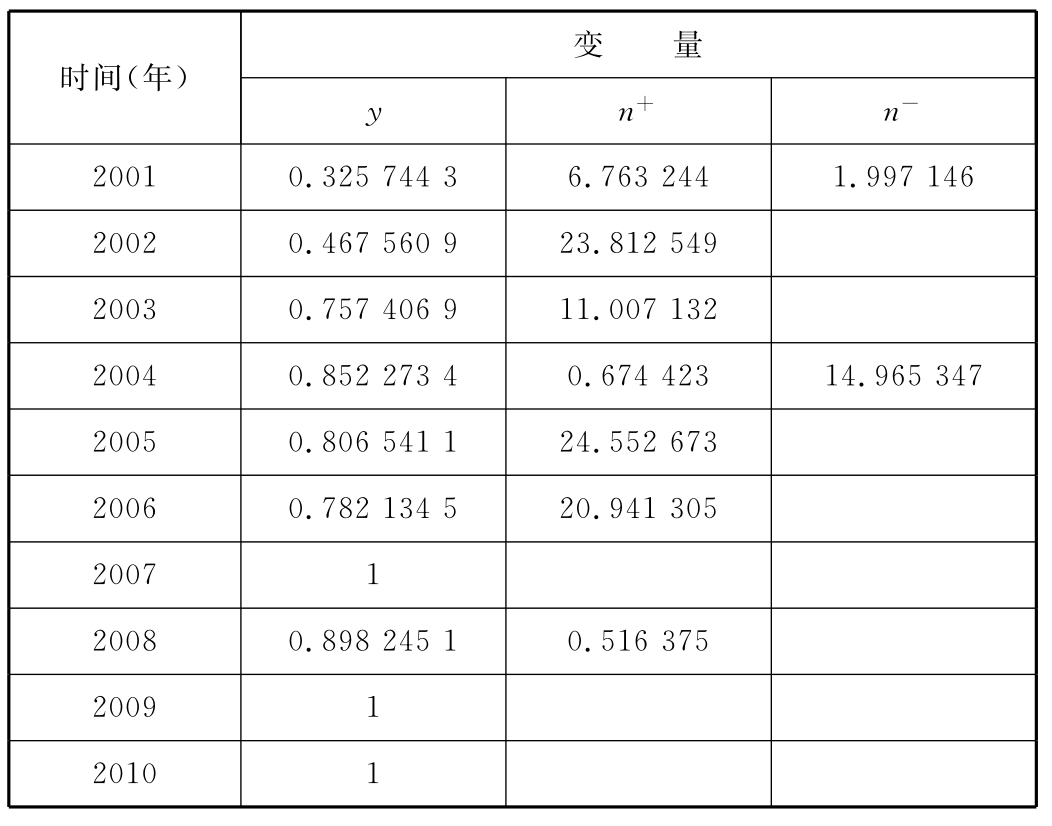
表5－1显示了样本企业的综合效率，我们可以看出在研究纵向边界的10年间，企业达到技术效率最优的只有3年，分别是2007年、2009年和2010年，其余各年都非效率最佳。从表5－1中的计算结果中可以很清晰地发现，该企业的技术效率被分成了较为明显的两个阶段:2001—2006年为第一个阶段，2007—2010年为第二个阶段。第一个阶段的数据显示，从2001年到2006年该企业的资源配置效率不高，投入产出量的不合理与企业整体结构不合理同时存在，几乎每年都存在技术创新投入过剩的现象，并且在2001年与2004年还存在环保投入利用效率低下的情况；而在第二阶段，4年中有3年达到了最优的生产效率，表明投入产出的配置合理，投入得到了充分利用，没有出现过剩与利用不足的现象。从这些计算结果可以看出，随着该企业进行循环经济的试验，在企业合作频度增加的情况下，技术投入、环保投入与产出的结构合理，配置效率达到了较优的水平，可以认为通过企业合作，使企业的配置效率得到提高。(www.xing528.com)

在表5－1显示结果的基础上，在预设的C²R模型中加入约束条件: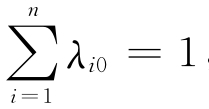，将C²R模型变形为C2 GS2模型以测量每一个决策单元的技术效率，在C²GS²模型中保持原有变量的含义不变，利用相同的数据再次进行计算，计算结果见表5－2。

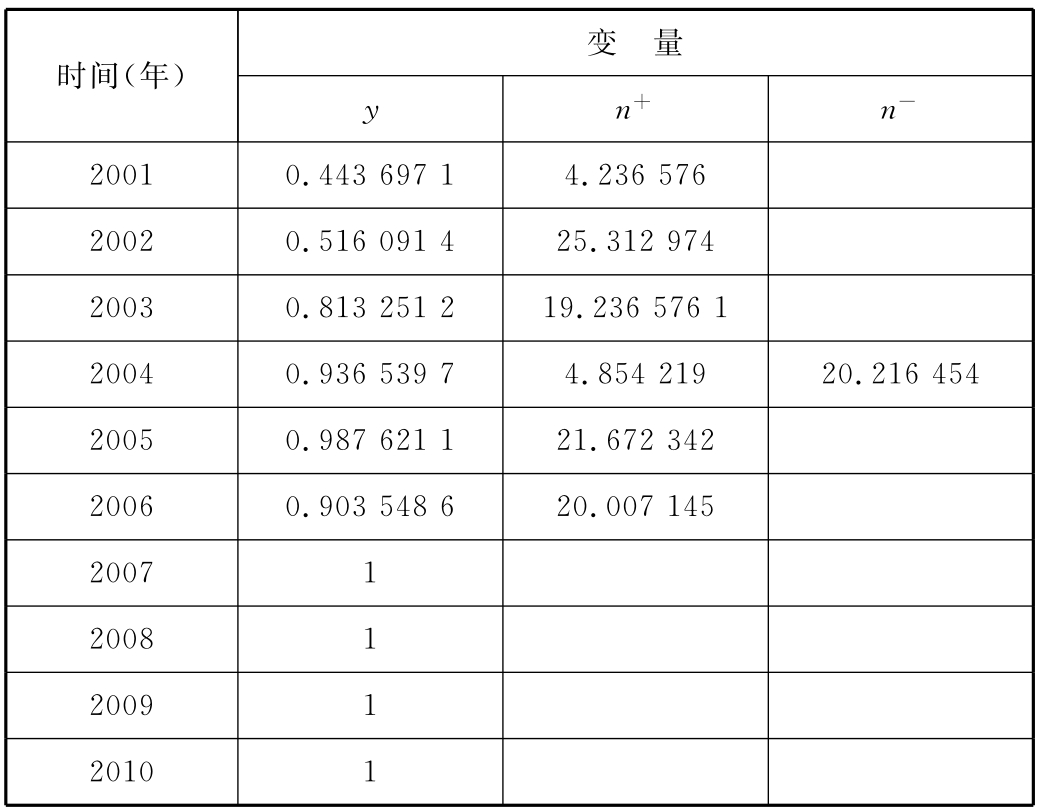
从计算的结果可以看出，第二阶段（2007—2010年）的技术效率均达到了1，且松弛变量都为0，表明不存在效率不足的现象，达到了技术效率最佳，各因素之间的配置处于最佳状态，DEA有效。第一阶段（2004—2006年）的技术效率接近最佳，存在技术投入利用效率不佳的情况。从这10年间的数据来看，该企业的技术效率保持了一种增长的态势。一般认为，技术在经济学的语境内，被认为是一种投入产出关系的具体体现，一般反映为生产函数，表现为生产过程中投入产出之间的某种数量关系。从计算结果的分布来看，可以看出该企业在实行循环经济试验之后其技术效率明显好于进行试验之前，通过有效的企业间的合作使企业的技术创新投入、环保投入与营业收入之间配置达到了最优。

表5－2　　　　　　C²GS²模型求解结果