刘 楠 张小勇
(信息工程大学电子技术学院二系,河南郑州450004)
摘 要 本文根据目前大学数学教学的现状和存在的问题,分析了数学教学中引入数学建模思想的作用和意义,提出了融入数学建模思想的案例教学模式,探究了该教学模式的主要构成因素,并对新教学模式的成效和不足进行了总结。
关键词 数学教学;数学建模;案例教学;教学改革
“高等数学”、“概率统计”等数学课程是高等教育中的重要基础课程,这些课程几乎涵盖了理工科大学中的所有专业,因此努力提高大学数学的教学质量具有十分重要的意义。传统数学教学以讲授方式为主,它主要注重学员对基础理论知识的掌握,而忽视了学员如何从实际问题出发提炼数学模型、解决实际问题等能力的培养。将数学建模思想引入到大学数学教学过程中,通过与学员专业或生活实际紧密相关的案例进行教学,既有利于激发学员的学习兴趣,又有利于提高学员的数学素养。这也与当今大学教育要全面提高学员素质、培养有创新精神的复合型人才的目标相吻合。
一、当前大学数学教学中存在的问题
数学课程是理工科大学中的重要基础课程,良好的数学基础是学习各类专业课的根本保证。目前很多高校都在数学教学上投入了大量课时,即便如此,很多专业课教员仍反映学员不善于利用所学的数学知识来解决实际问题。造成这种情况的主要原因如下:
(1)各类数学课程内容多,教材陈旧,教学手段单一。课堂教学中一般只注重数学概念、理论及计算方法的讲解,因而牺牲了对数学知识背景和应用的介绍,更缺少对实际问题的假设、抽象和模型建立等数学思维方面的训练。
(2)各高校都比较注重教学内容、手段和方法的改革,而忽视了教学模式的改革。传统的教学模式是以教员为中心展开的,学员处于被动接受知识的地位。在这种模式下,作为认知主体的学员往往缺乏学习的自主性和能动性,因此,很难达到理想的教学效果,也不利于创新型人才的培养。
(3)在考核形式上主要以书面答卷为主,在内容上特别注重对公式和结论的巩固、推理,这种评价方式忽视了对学员学习过程和解决实际问题等能力的考查。
二、数学建模思想的特点与作用
数学建模是运用数学的思想、方法和手段对实际问题进行抽象和合理假设,建立起反映实际问题内在数量关系的数学模型,然后运用计算机技术对数学模型进行求解,再用求解结果去解释、分析实际问题并对数学模型进行验证和修改。数学建模一般没有统一的方法,但是其处理实际问题的过程大体相同,主要包括以下几个步骤:模型准备、模型假设、模型建立、模型求解和分析、模型检验和修改。
数学建模源于1985年在美国创办的大学生数学建模大赛,经中国数学教育工作者的组织和推动,1989年我国几所大学的学生开始参加这项竞赛。1992年中国工业与应用数学学会将大学生数学建模竞赛引入国内,从此每年举办一届,十几年来这项竞赛的规模以平均年增长25%的速度发展。在数学教学中引入数学建模思想,既有利于使学员巩固所掌握的数学知识,又有利于在教学中贯彻理论与实际相结合的原则。这种教学方法可以极大地提高学员的学习积极性,还能培养学员的协作精神和创新意识。
融入数学建模思想的教学以提高学员数学素养和分析问题、解决问题的能力为目标,以联系生活实际和社会实践的案例为教学材料,教学过程中强调以学员为中心,注重师生的交流和互动。这种教学模式符合建构主义的认知理论,是大学数学教学改革的重要方向。
三、融入数学建模思想的案例教学
为了利用数学建模的思想来提高学员的综合素质和实践能力,一般可以在学习了课程的一章或一个独立的知识要点之后进行一次案例教学。我们设计了融入数学建模思想的案例教学模式(如图1所示),它主要涉及教员、学员和评价方式三个主要方面,现对这几个方面的作用及实施要点分析如下。
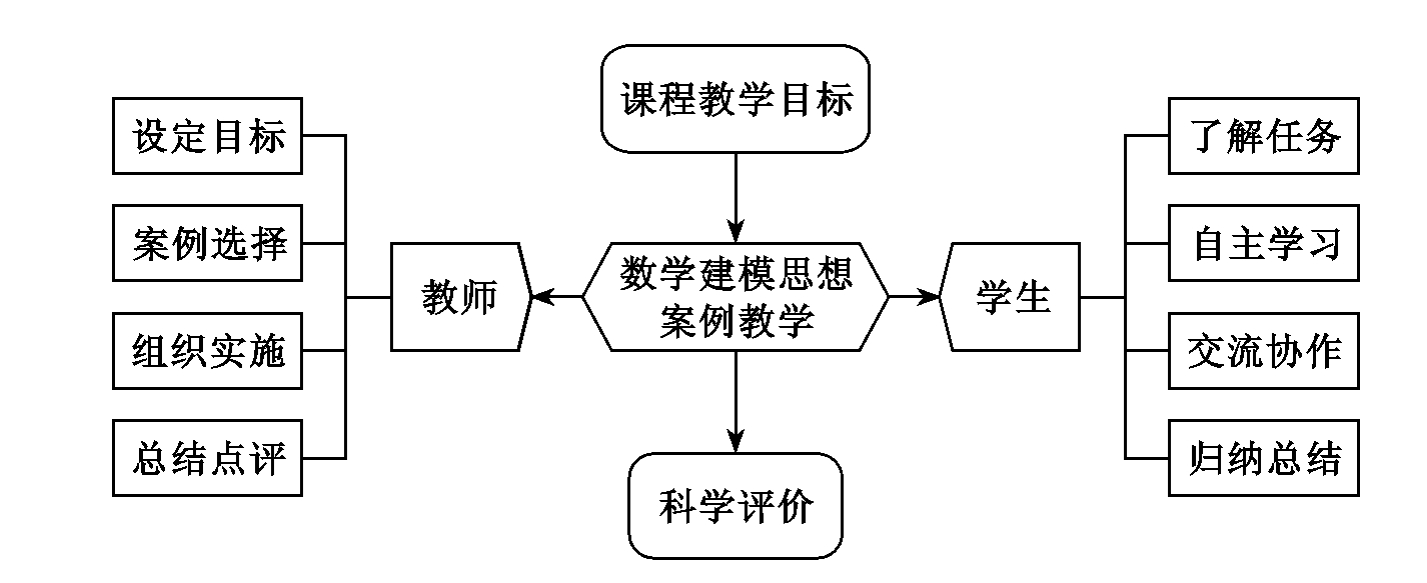
图1 融入数学建模思想的案例教学模式(https://www.xing528.com)
(一)注重教员的引导作用
在案例教学过程中教员不再是知识传授的权威,但仍然是教学过程的组织者和引导者。教员要根据一定的教学目标,选择符合学员能力层次、重点和难点突出并与生活实际紧密结合的教学案例。教员还应负责组织学员开展案例讨论,引导学员积极思考、合理利用相关学科的知识,从而实现从传统“教教材”到引导学员“用教材”方向的转变。另外,在教学过程中教员也需要浏览学员所搜集的资料,及时了解学员对问题解决方案的产生过程,通过与学员的共同研讨不断提高自己,从而实现教学相长。
(二)调动学员的参与热情
融入数学建模思想的案例教学中,学员不再是知识的被动接受者,而是教学过程的积极参与者,是知识建构的主体。与实际问题紧密结合的教学案例,兼具知识性和趣味性,因而能够激发学员的学习兴趣,调动学员的主观能动性。
比如在《高等数学》下册第十章高斯公式一节,传统的方法只是给出高斯公式的结论及其证明,至于其应用都是直接的积分计算,没有一定的实际背景,学员在学习的过程中只是就题论题,缺乏一定的趣味性,这样效果就不会很好,可能当时能够掌握但是很快就会遗忘;而如果在这里引用初中阶段学员就已经了解的阿基米德浮力定律一例,就会达到很好的效果,不仅加深对高斯公式本身的理解,还可以使学员直接感受高斯公式的实际应用。因为阿基米德浮力定律的证明过程需要首先简化条件,建立数学模型,进而把对坐标的曲面积分通过高斯公式转化为三重积分得出最后的结论。这个过程要求学员先把实际问题转化成数学问题,也就是建立模型的过程,能够很大程度的激发学员的兴趣,再通过对公式的应用解决问题,一举两得。
在具体实施过程中,学员可以以小组为单位通过交流、讨论等方式寻找问题最合理的解决方案。在此过程中不仅增强了学员的自主学习意识,还能使学员注重在小组内进行有效的分工和协作,从而创造性地解决实际问题。
(三)改进传统的评价方式
传统的数学教学评价方式以书面考试为主,它更多地关注学员的计算能力,属于“注重结果”的评价方式。引入数学建模思想的案例教学,其内容、形式和过程都较传统教学模式有很大变化,因此相应的评价方式也应该从“注重结果”改变为“关注过程”,从而建立更科学的多元化的教学评价方式。
好的教学评价方式是促进教与学的重要手段,有利于帮助发现教学中存在的问题,使教员和学员进行自我反思和总结。“关注过程”的评价方式主要包括以下几个方面:学员在小组讨论过程中的表现;学员在分工协作中所负责的任务及其完成情况;学员将实际问题转化为数学模型的思想方法及计算机编程能力;解决问题的方案、报告的组织和表达等。
四、结语
融入数学建模思想的案例教学是一种新的教学模式,它能带动学员自主学习的积极性,注重提高学员分析问题和解决问题的能力,也可以培养学员的协作精神和创新意识,实际教学中受到了很多学员的欢迎。尽管如此,这种教学模式仍然有很多局限性,例如,适合教学的案例很难选择、教学实施过程花费的时间较多、教学的开展容易受学员知识和能力水平的限制等,因此在大学数学教学中开展案例教学还需要更多的尝试和探讨。总的来说,在大学数学教学中,融入数学建模思想的案例教学是对传统教学方法的有益补充,只有把两方面有机地结合好,才能启迪学员的积极思维,调动学员主观能动性,达到很好的教学效果。
参考文献
[1]张华.课程与教学论.上海:上海教育出版社,2006.
[2]杨启帆.数学建模.北京:高等教育出版社,2005.
[3]李大潜.将数学建模思想融入数学类主干课程.中国大学教学,2006(1).
[4]于珍.数学史与高等数学教学.河北农业大学学报(农林教育版),2008(3).
[5]郭德红.案例教学:历史、本质和发展趋势.高等理科教育,2008(1).
[6]张顺燕.数学的思想、方法和应用.北京:北京大学出版社,1997.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




