探索概率论教学中思维方式的培养

浅谈概率论教学中思维方式的培养

张小勇　刘　楠

(信息工程大学电子技术学院二系，河南郑州450004)

摘　要　概率论教学的目的之一就是要培养学员科学思维方式的转变，同时也正是由于概率论独特的思维方式造成了概率论学习的困难。本文从教学实践出发，对概率论的教学过程中随机性思维、统计思想以及创造性思维的培养问题进行了探讨。

关键词　概率论;思维方式;教学

概率论作为本科期间唯一一门研究随机现象的课程，不仅为学员提供了必要的数学知识，而且为其他后继专业课程的学习提供了重要的理论基础，其重要性不言而喻。而概率论作为一门从实践中发展起来的重要学科，不同于数学分析、高等代数等研究确定性现象的纯粹的数学学科，它需要思维方式从确定性到随机性的转变。从教学目的看，这种思维方式的转变本身就是概率论教学所要完成的任务之一;从教学实践看，也正是由于这种思维方式的独特性，使得学员在学习和掌握这门课程时普遍感到概念抽象，解决问题的方法难以掌握，学习起来比较吃力。所以，思维方式的培养对本门课程的学习是至关重要的。本文从我院概率论的教学实践出发，对概率论的教学过程中学员思维方式的培养问题进行探讨。

一、在教学中贯穿随机性思维方式的培养

概率论作为一门研究随机现象规律性演绎的学科，需要科学思想从确定性思维到随机性思维的转变，学员由于习惯了在“高等数学”和“线性代数”等先期课程中的绝对确定性的数学思维模式，故在初学概率时往往不易接受，因此采取何种教学手段，引导学员从传统的确定性思维模式进入随机性思维模式，是成功教学要解决的一个首要问题。在教学实践中，笔者做了以下几个方面的尝试:

(一)从课程开始就让学员尝试理解随机现象的真正含义，理解必然和偶然的关系

随机现象是一种客观存在，是无法否认的。尽管对于一个偶然现象的认识可以越来越精确，但是无论如何，都不可能完全准确的预言。这是因为，影响一个现象的因素是大量的，而且这些因素之间的关系是错综复杂的，没有办法把所有的因素都确定化。以前所学习的确定性的数学模型，无一例外都是在忽略了许多次要的因素之后建立的。此外，还要学员理解必然和偶然之间是哲学上对立统一的关系。“偶然”绝非碰巧，它有着内在的规律性;反之，“必然”也是由纯粹的偶然所构成的。

在实际教学中以实弹射击为例进行讲解。影响射击成绩的随机因素很多:空气的温度、湿度、气压、风向风速、枪支不可控的抖动、射击者的情绪波动等。所以有些时候尽管瞄得很准，也会出现脱靶等意料之外的情况。但是，一个射击成绩优秀的学员，绝不可能是完全靠运气就能每次都取得好成绩，原因是在长期的训练中对一些重要的随机因素的规律把握得比较好。这样的实例结合了军校学员的特点，学员都有切身的体会，理解起来比较容易，取得了良好的教学效果。

(二)要理解不确定性思维，必须理解概率的真正含义

笔者认为，理解概率关键是要理解某一事件发生的试验频率与理论概率的关系。概率论告诉我们，不确定性的事物尽管其变化具有随机性，但可以通过测算其发生的可能性来认识和研究事物。

这里，首先要讲述清楚可能性的含义，这可以从现实的例子给学员以直观的感受。比如说:抛硬币的试验，我们总是说在一次试验中出现正面的可能性是1/2，那么到底所谓可能性是什么含义?此时必须做如下解释:尽管在一次抛硬币时，结果只能有一个，但是如果反复将同一个硬币抛很多次，大约各有一半的次数出现正面，一半的次数出现反面。虽然无法预言这一半的次数具体是哪几次，但总次数的比例却是可以预言的。

其次，用什么指标来描述这种可能性?这需要逐步启发学员。从直观意义上讲，频率可以描述一个随机事件在一次试验中发生的可能性，但是直接用频率描述是有缺陷的，又考虑到频率本身的稳定性，故用频率所稳定到的固定常数——概率来描述。然而，在实际中，要想通过这种大量试验来确定概率的方法是不可行的，故给出了如古典概型、几何概型等数学方法来计算概率，甚至在某些情况下，我们就用频率来代替概率进行近似计算。只有让学员真正理解了概率的本质含义，才能理解为什么“概率为0的事件不一定是不可能事件，概率为1的事件不一定是必然事件”，才有可能对概率的公理化体系以及大数定理和中心极限定理等理论知识有较为深刻的理解。

在实际教学中，要求学员用C语言编程对英文文档中各个字母出现的频率进行统计，并观测随着统计的文档的增加，各个字母出现的频率有什么规律。这样的课后作业既锻炼了学员的动手能力，又加深了学员队对于概率概念的理解。

(三)必须把不确定性思维在教学过程中不断地强化和巩固(www.xing528.com)

在教学中，培养学员习惯于“某个事件以多大概率发生”这样的描述方式，而不是总以抱着固有的数学分析或者高等代数等确定性的思考方式来研究随机现象。

在讲述随机变量时，一定要强调随机变量与数学分析中所学过的变量相比，其取值随机性这样一个特性。如:ξ= k是一个随机事件，可以计算P(ξ= k)，这样的计算在数学分析中是不存在的。再如:对于结论

D(ξ)= 0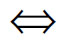P(ξ= Eξ)= 1，

其充分性是显然的，但是对于必要性的理解学员往往会陷入“P(ξ= C)= 1就意味着ξ每次只有一个取值C，从而必要性成立”错误的推理过程。讲解相关系数时候，“两个变量以多大概率存在线性关系”的说法和学员先期课程的学习中所得的固有印象有较大差别，此时，必须做以下解释:此处的两个变量都是随机变量，从而两个变量之间存在线性关系就是一个随机事件，必须用概率来测量其发生的可能性。

只有这样，才能使学员真正理解现实世界广泛存在的随机性，并主动将其应用到实际生活之中。

二、在教学中渗透“统计思想”的培养

概率论和数理统计都是研究随机现象统计规律的学科，有人称它们为“姐妹篇”，但是二者虽然有共性，但个性也相当突出。概率论偏重于基础理论，是对随机现象统计规律演绎的研究，而数理统计则偏重于研究应用，是对随机现象统计规律归纳的研究^［1，2］。虽然两者在方法上是如此的不同，然而两者确实是相互渗透、互相联系的。我院学员虽然仅仅学习概率论部分，但是在后续课程如密码学的学习中，经常会遇到诸如参数估计，假设检验等内容，甚至用到了Markov链等随机过程的知识，而这部分知识的学习仅仅靠学员的自学是不够的。从笔者的调查来看，学习效果不甚理想。这是因为概率和统计在学习方法上有较大差别，自学的确存在困难，但是培养方案又不允许分配给数理统计部分专门的课时，所以，必须在概率论的教学过程中逐步灌输一些数理统计的思想，掺杂一些数理统计的例子。

在讲授古典概型的时候，笔者举了这样一个例题:假设某接待站一周有十次来访，均发生在星期二和星期四，问来访是否有时间规定?对于该题目，初次接触的学员甚至都不认为这是一个数学问题，因为在他们的印象中，这样的问题似乎无法用数学方法解答。首先提示学员考虑概率的本质含义，既然概率是衡量一个随机事件发生的可能性大小的度量，如果概率很小那么就意味着这个事件在一次试验中不应该出现，这就是所谓的“实际推断原理”。然后，运用反证法的思想:假设来访没有规定，那么来访是随机的，于是根据古典概型，“来访均发生在星期二和星期四”这一随机现象发生的概率为(2/7)10，这是一个小概率事件，根据实际推断原理，是不应该出现的，现在竟然出现了，那么就有理由认为来访没有规定这一假设是错误的，从而来访是有时间规定的。这个问题的讲述中实际上已经让学员初步接触了实际推断原理和假设检验的思想，同时也激发了学员的学习兴趣。

实际上，这样的例子在概率论部分还有很多，比如说独立同分布的随机变量序列已经暗含了统计部分的母体与样本的性质，辛钦大数定理实际上给出了样本的均值与母体均值的关系，等等。

三、在教学中强调“创造性思维”的培养

概率论也是一门应用性很强的学科，不仅要在理论的学习上实现思维方式的转变，同时也要注重培养学员应用概率知识解决实际问题的能力，培养学员的创造性思维。在教学中，尝试开展“体验式”教学，使学员不仅学会知识，更重要的是学会知识的运用，提高分析问题的能力。要善于从身边的生产、生活入手，机智、巧妙地编拟成学员喜闻乐见的题目，通过实际问题的引入，一方面加深学员对概念的理解，另一方面可以使学员认识到“数学来源于生活”。在讲授知识时，使学员尽可能“回归”到实际背景中去，这将有助于培养学员的实际操作能力及建模能力。

如在讲授Poisson分布时，可以让学员在某个马路口，观察一段时间内所通过的汽车数量，看其是否服从Poisson分布;在讲授正态分布时，可以结合某次小考，让学员统计成绩的分布，画出直方图，这样不仅有助于学员对正态分布性质的理解，同时认识到直方图就是离散化的分布密度函数，这对于以后的工程实践是大有帮助的。

在概率论的授课过程中，注重思维方式的培养，使学员正确地去思考、认识和处理生活中的现象，不但能够增加这门课程的知识性、趣味性，同时还能够使学员从“要我学”变成“我要学”，从而取得良好的教学效果。

参考文献

［1］梅雪晖.概率论与数理统计教学探究.长春师范学院学报(自然科学版)，2009(8): 114-116.

［2］魏悦姿，姚玉平.概率统计教学中培养学生实践能力和创新素质的探索.吉林省教育学院学报，2009(2): 92-94.