不确定环境下资本结构研究成果

第三章　风险债务估值与不确定环境下的资本结构

企业的资本结构决策必然牵涉到有关利益主体的利益，特别是股东与债权人的利益，这里，我们假定资本结构决策由企业管理者做出，正如我们在前面讨论的，企业管理者一般会按照股东的意愿即使股权价值最大化目标行动。然而，MM定理指出，在严格的MM框架下，无论管理者怎样做出有关资本结构决策，均不会影响企业价值。这个出人意料的结论即使在有风险（但无破产成本）的情形下，正如第二章所指出，也可能是正确的（无税收）。其含义是只要企业现金流不流向除股东与债权人之外的第三者，企业价值就不会发生变化。令人遗憾的是，企业破产（清算与重组）往往是市场经济的必然现象，伴随着这些企业的破产，必须伴随着破产成本（或财务危机成本）的产生，这不仅影响股东的利益（一旦企业破产，股权价值为0），还影响债权人的利益，因此，现代公司财务理论中的一个重要研究领域是关于公司债务的估值理论，特别是布莱克—舒尔斯与默顿的期权定价思想，即默顿称之为相机权益分析（Contingent-Claims Analysis，即CCA）方法，极大地丰富了公司财务理论。而将风险债务估值与不确定环境下的资本结构结合起来研究，尚不多见，本书这一章将运用CCA方法研究资本结构问题，并对现有的一些资本结构理论及观点提出新的解释。

3.1　概述

自现代资本结构理论出现以来，一直困扰金融经济学家的问题是是否存在最优资本结构，决定最优资本结构的要素到底有哪些？经过几十年的探索，目前这个问题仍未得到明确的答案。^[1]在本书第二章，我们已全面评述了现有的大多数资本结构理论，其中绝大多数是定性或通过实证分析出资本结构的决定要素，从不同角度得出相应结论。正如在评述中所指出，各种要素最终影响的是各方的利益，而各方索取者利益的直接表现是各种证券的价值，因此，证券特别是股权证券与债务证券的价值评估会直接影响到企业的资本结构决策，反过来，各企业的资本结构决策也会直接影响企业各类索取权（Claims）的估值，从而决定各方的利益。由于各方的理性预期，^[2]资本的决策必须能够反映持有各类索取权的投资者的要求，通过不断修正，最终可能达到最优资本结构。因此，理性预期是我们这一章的基础，即企业价值、股权价值、债务价值反映了各方的理性预期，从而决定其投资策略。这种通过证券均衡定价得到的定量分析往往比前述的定性分析更有力，特别地，由于有公司债券市场，公司债券的交易价格可看做是投资者的理性预期值，用这些交易数据可以检验理论的合理性。

正如我们在2.2.2中所指出的，按照默顿的观点，债权人持有的债券实际上可看做是一个无风险债券减去一个欧氏看跌期权，或者加上一个看跌期权的空头，这个看跌期权实际上是股东有权违约，其付出的代价是把企业现有资产交由债权人，债权人可以继续经营，也可以清算资产。因此，实际上债权人持有的债务资本的价值依赖于企业资产的价值，需要说明一下的是，这里企业资产的价值可假定不依赖企业的资本结构，即相当于一个完全股权所有的企业资产价值。由于企业资产在经营过程或市场环境下，会变大或变小，即发生变化，因而公司债务价值也非固定，从而是有风险的。企业资产价值实际上决定了公司债务价值，公司债务可看做是企业资产价值的相机权益（Contingent Claim）。当企业经营状况好，企业资产价值远远高于公司债务面值时，股权资本提供者无须违约，此时公司债务得到全部的承诺，即利息与本金支付，公司债务无风险；当公司经营状况不好时，企业或缺乏必要的现金来支付利息或企业资产严重贬值，使得企业资产价值比公司债务的面值低，则股东违约或债权人强制企业破产，此时债务资本提供者获得企业资产的所有权，即债权人拥有公司的所有剩余，而股东可能得不到任何价值。公司债务有风险，从而看跌期权有正价值。特别地，当企业破产清算时或企业重组时，会有破产成本支出，实际上，债权人只能得到部分剩余，因此破产成本对公司债务价值影响很大。公司债务价值是公司价值的重要部分，在不考虑股权代理成本时，股权价值是公司价值扣除公司债务价值后的剩余，因此，从股权价值最大化角度，我们可以决定一个最优资本结构，而从企业价值最大化角度，我们又可以得到一个最优资本结构，这其中的差异可认为是由类似于“资产替代效应”所产生的债权代理成本，只不过这里是对资本结构进行的次优决策，而不是对投资项目进行的次优决策所产生的低效率。

公司债务的这种相机权益（Contingent Claim）性质，使得我们可以充分利用已有的相机权益分析技术，虽然默顿在B-S公式（即布莱克—舒尔斯公式）推出后第2年即1974年就用其对公司债务定价，并讨论了MM定理，开创了用相机权益分析方法研究资本结构的先河。然而其结论也并非十分完善，与实证分析也不太吻合，主要是因为默顿假定破产是外生的，而且债权人具有绝对的优先受偿权，未考虑破产成本。正如我们在前面所指出的，由于股东有经营决策权，其会充分利用手中的权限，尽量拖延破产，榨取企业价值，从而损害债权人利益。Franks与Torous（1989）通过实证分析指出，在许多破产案例中（他们选择了30家破产企业的样本），股东实际接受了一些支付，通常是证券，而类似的工作，Weiss（1990）发现在其研究的样本中，1/3企业的股东在破产后新重组的企业中获得了超过25%的股权。而实证发现实际上公司债的风险费（Risk Premia）显著地高于Merton模型所暗示的，因此，必须对Merton的模型进行改进。为更好地理解资本结构，在股东与债权人的利益冲突下，运用相机权益分析方法，在与实证分析相吻合的假设下得出一些新的启示是本章的出发点。

利用相机权益分析技术得到的资本结构与公司债务估值的结果对于解决转轨经济下的国有企业债务问题是很有帮助的。目前，对于国有企业沉重债务负担的化解，已成为牵动和影响国有企业改革的关键性问题，通过资本市场，通过债务托管机构要化解这些不良债务，不可避免地要牵涉到这些债务的估值问题。只有解决了公司债务的估值问题，才可能实现不良债权的证券化和市场化，也才能对各种债务进行重组，使各利益主体均能接受。而资本结构对公司债务价值的影响也必将反映在企业管理者的资本结构决策中，从而达到优化资本结构的目的。

为了分析，我们作如下假设。第一，企业所面临的不确定性环境是“共同知识”，企业管理者（我国公司法称之为经理）及各类投资者一样清楚，从而我们排除了关于不确定性的信息不对称。第二，企业管理者及各类投资者对企业价值组成有理性预期，他们能够准确计算企业负债带来的税收优惠及相应而产生的财务危机成本，也就是说，这两者是决定资本结构的重要因素。因此，企业管理者或股东在作资本结构决策时，考虑到了不同资本结构带来的好处及坏处，从而能够准确决策，不存在融资决策的冲动或盲从。第三，我们本章不考虑企业管理者与股东的利益冲突，即不考虑1.3.3中詹森与麦克林所指出的股权代理成本，也不考虑资本结构对降低股权代理成本的作用。因此，这一章我们可把企业管理者与股东当做单一的个体，可以使我们集中研究风险债务估值与资本结构的关系，即债权人与股东的利益冲突。第四，无论资本结构如何变化，企业的资产价值（相当于完全股权的企业资产价值）是外生的，^[3]其不依赖于资本结构，从而排除了1.2.3所说的某些财务危机的间接成本以及1.3.3中Titman所指出的企业生产的产品类型与资本结构的关系。

本章的主要内容是破产成本对风险债务估值有显著影响，借助于CCA方法，我们得到了风险债务估值公式，其对最优资本结构的研究至关重要。我们把这一公式运用到纯混合兼并，考虑了纯混合兼并后债务价值的变化。通过对最优资本结构的研究，我们得到影响最优资本结构的企业内部特征是企业的投资政策、股利政策、破产后资产的流动性即破产成本特征，而外部特征为企业所得税税率、无风险利率，这五个因素共同决定了企业资本结构。

本章安排如下。在3.2中我们讨论了风险债务估值。特别地，我们推广了Merton或Black ＆ Cox关于公司债务的定价，在一个新的破产安排下，得到了一个公司风险债务估值的解析表达式，并且我们把这一结果运用到纯混合兼并中，分析了纯混合兼并对公司债务估值的影响，从而得出纯混合兼并不一定能改善企业的债务状况的结论。在3.3中我们建立了不确定环境下的资本结构模型，通过模型分析内生破产点与最优资本结构的关系，并给出影响资本结构的各要素与最优资本结构的比较静态分析结果，通过该模型，能够定量刻画我们在第一章所介绍的一些定性观点与理论，从而更具说服力。3.4为本章小结。

3.2　风险企业债务估值研究

期权定价理论的推广如默顿所指的相机权益分析（即CCA）方法是研究风险企业债务价值的重要工具，这一节我们运用该工具推广默顿（Merton，1974）的工作，并把其运用于下一节资本结构问题研究中。风险债务与无风险债务的估值有显著差异，正如对股票估价我们常用股利贴现模型一样，对无风险债务由于其有固定的利息与本金支付，也可以用收入资本化方法贴现求得其价值，然而正如股利贴现模型一样，对无风险债务的利息及本金贴现必须考虑贴现率，贴现率是决定这些确定性模型的重要因素。风险债务估值不仅其收入流是不确定的，往往其贴现率也不确定，因此往往得不到一种解析表达式。为简单起见，我们在本章大多不考虑贴现率即利率的变化，特别地，我们不把其作为随机的。^[4]这样能使我们专注于资产价值的不确定性对债务价值的影响。

3.2.1　无破产成本的风险债务估值

公司债务与国债一样，是一种重要的金融资产，其价格行为远远比国债的价格行为复杂，我们一般认为国债不存在违约风险，而公司债务存在违约风险。由于存在违约风险而产生的收益利差（Yield Spreads）往往是研究公司债务的出发点，人们之所以愿意购买有违约风险的公司债务，承担相应风险，就是因为能够获得高于国债收益的风险费，因此，运用CAPM可以解释公司债务之所以存在的理由。各种资产的风险不同，从而其需求与供给也不同，从整个金融市场角度出发，公司债务代表着一类重要金融资产，是金融市场不断完善的结果，这是从宏观（Macro）角度考虑公司债务定价或利差。Jaffee（1975）从这个角度把公司债务的相对价格或利差看做是各种资产供求以及经济周期的函数，是这方面研究的一个代表。另一方面，也可从微观（Micro）或企业特征角度讨论公司债务价值，把企业债务价值看做是企业特征如企业财务或经营风险的函数，不同企业由于经营风险（市场或经济的不确定性）及财务风险不同，企业债务价值也就不同，从而不同企业的债券利差不等，这方面最初由Fisher（1959）提出，Fisher虽然未能使用相机权益分析工具，但后来的相机权益分析与Fisher的分析是一致的，CCA的优点在于可以直接提供一个函数可供实证检验，有时能得到解析解。

企业面临的财务风险与经营风险，直接影响企业对公司债务的违约可能性，并且也会改变企业一旦违约，债权人所能得到的补偿，因此，其直接与债务价值有关。这里暂不考虑破产成本（既包括直接破产成本，也包括间接破产成本），去寻找与公司债务价值有关的因素。

CCA文献中的假定大多大同小异，其中最重要的几个假定如下：

假定1：“关于金融市场的假定。”

存在一个完美（Perfect）、无摩擦（Frictionless）金融市场，证券可以连续交易。没有交易成本或交易税，允许卖空，借贷利率是相等的，任何个人对金融资产的买卖不影响市场价格。^[5]

假定2：“关于无风险资产的假定。”

存在一个无风险资产，其单位时间的回报率是已知的，且为常数，记为r，其不随时间而变化或按照Merton（1974）的假设A.7的说法，期限结构（Term-structure）是平的（Flat）且是确定的。^[6]

假定3：“关于企业资产价值动态性的假定。”

企业资产价值（独立于资本结构，即一个完全股权企业资产的价值）可描述一个扩散的随机过程，该随机过程可用随机微分方程表示：

其中W是一标准布朗（Brown）运动或dW为高斯—维纳过程（Gauss-Wiener Process）。α是企业资产单位时间的瞬时预期回报率，σ2是企业资产单位时间回报的瞬时方差，其反映资产回报的波动。C是企业单位时间的支付，如其大于0，则可看做是企业支付给股东（股利）或支付给债权人（利息），如其小于0，则表示为企业通过新融资（股权或债务融资）得到的净资本。^[7]

假定1与假定2对于构造无套利证券组合是必不可少的，只有通过无套利条件，才能对企业各类证券均衡定价。实际上，由于牵涉到随机微分方程（假定3），其主要使用的工具为伊藤引理（Ito’s Lemma）^[8]，对Ito过程的微分不同于一般函数的微分。运用Ito引理，就可导出关于企业证券价值的Black-Scholes微分方程。

下面我们来考虑公司债估值问题，假设公司仅有两类索取权（Claims），即一类剩余索取，股权，而另一类为单一债务（这里不考虑不同类型债务如可转换债等）。显然两类索取权的价值均依赖于企业资产价值V，如Merton（1974），设企业某种证券价值Y可写作Y = F（V，t）形式，Y的动态性同样可写作一随机微分方程。

类似于式（3.1）中参数的解释，这里αy表示该证券单位时间瞬时预期回报率，是其瞬时方差，Cy为该证券单位时间的支付（股利或利息），dWy为一标准高斯—维纳过程。^[9]

由于Y = F（V，t）为V的函数，而V本身服从方程（3.1），故Y = F（V，t）为Ito过程，对其运用Ito公式可得到αy、σy、Cy、Wy与α、σ、C、W等之间的关系，实际上，由Ito引理，对Y求微分，并由式（3.1）可得：

其中下标表示对F的偏导数，比较式（3.2）与（3.3），则立即有：

实际上，通过构造无套利证券组合，可以得到超额收益率之间的关系：

或

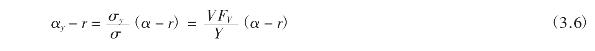
运用式（3.4.a）及Y = F，则式（3.6）立即有：

移项得：

此即证券价值Y = F（V，t）所满足的偏微分方程，该式类似于布莱克—舒尔斯在导出期权定价公式中得到的B-S微分方程，因此这种分析可看做是B-S分析的推广。当然，正如在得到B-S公式一样，要完整描述F（V，t），还必须给出式（3.7）的边界条件与初始条件，这往往依赖证券本身的特征，也正是这些边界条件使得不同证券有所区别（如债务区别于股权）。

仔细观察式（3.4.b）与（3.6）会发现，VFV/F是一重要比率。实际上这是一个弹性系数，把FV写为坠F/坠V，就可看出。在（3.4.b）中，它把证券回报的瞬时标准差与企业资产回报的瞬时标准差联系在一起，而在式（3.6）中，它把证券瞬时回报率与企业资产瞬时回报率联系在一起，因此可以说该弹性系数传导了关于相对风险与预期回报的基本信息。另外，由式（3.7）也可发现，企业证券的价值与α无关，只与σ2有关，这被称之为风险中性定价。

Merton（1974）在式（3.7）基础上讨论了风险贴息债券的定价，公司贴息债券是指企业在债务到期前并不支付利息，而是到期支付面值B，因而到期前的价格低于其面值。默顿假定，一旦公司到期违约，债券持有人（即债权人）立即接受公司（无破产成本），而且在到期前，公司不能发行新债务或支付股利，损害债权人利益。假定Cy= 0，C = 0，设T为到期日，令τ= T - t，则Ft= -Fτ，则公司债务价值F（V，τ）改写为：

其边界条件与初始条件为：

由式（3.8）及边界条件（3.9）可立即用富利叶变换（Fourier Transforms）求解F，实际上也可以直接利用期权定价的B-S公式，先求股权价值f（V，τ），再由F（V，τ）= V - f（V，τ）求出债务价值。f（V，τ）由下式给出（Merton，1974）

其中：Φ（X）为标准正态分布函数，

从而有：

其中：

可以证明通常小于或等于1，默顿定义风险债务的风险费为R（τ）- r，其中R（τ）由下式决定

则由式（3.11），立即有：

可以看出风险费仅仅是两个变量的函数，一个变量为σ2，表示企业经营的波动；另一个为L，表示一种债务与企业价值的比率，为承诺支付的现值（以无风险利率贴现）与企业价值的比，默顿称之为“准”债务比率，Merton（1974）所作的比较静态分析指出，风险费R（τ）- r是关于L与σ2的增函数，这与式（2.42）得到的结论是类似的。并且考察债务应得的预期回报率αy与市值的债务/股权比率即F/f = F/（V- F）发现，αy开始是F/f的一个凸函数（Convex Function），而随着F/f值上升，αy经过一个拐点，变为F/f的一个凹函数（Concave Function），而当F/f→+∞时，αy→α。

不同于Merton（1974）的工作，Black ＆ Cox（1976）从安全契约条款角度讨论了贴现债券的估值问题，这里安全契约条款是指债权人有权在企业价值落在一个较低水平时强迫破产或重组，并立即得到企业资产所有权（也无破产成本），而不必如Merton（1974）所假定的必须在到期日实施。在这种情况下，利息支付将不起关键作用，因而Black ＆ Cox（1976）也仅考虑贴息债券，但他们允许企业支付股利如dV，他们给出了特别的破产水平或重组边界为Ce-V（T - t）。设该债务价值为B（V，t），而到期面值为P，运用首达时的分布，得到如下复杂公式：

其中：

在有安全契约条款时，B（V，t）是V与t的增函数，是σ2，r，d的减函数，特别地选择Ce-v（T - t）=ρPe-v（T - t），0≤ρ≤1，则容易由式（3.13）验证B是ρ的增函数，因此，债权人总是希望尽可能快地破产，使债务价值更大。B不仅是ρ的增函数，而且还是ρ的凸函数，并且随着ρ→1，因此破产水平越高（ρ越大），债务会越安全。

Merton（1973）与Black ＆ Cox（1976）为我们研究了债务估值甚至资本结构提供了强有力的分析工具，即CCA方法，但他们的结论并不令人满意。正如在3.1中所指出，由于债权人只能在债务到期采取行动（Merton，1974）或达到一个较低的重组水平采取行动（Black ＆ Cox，1976），而且债权人大多是直接接管企业，取得企业资产的完全所有权，从而债权人的损失相对有限。实际上，他们均未考虑破产成本或重组成本，也未考虑公司所得税，认为债权人具有绝对优先权，这一切都使他们的结果有可能偏离实证结果，正如Jones，Mason and Rosenfeld（1984）与Franks ＆ Torous （1989）所表明的，上述模型暗示的利差远远小于现实债券市场的利差，因此债权人一定在其他方面可能有很大损失。下面我们重点考察破产成本对债务估值的影响。

3.2.2　有破产成本的风险债务估值研究

破产是一种法律机制（Legal Mechanism）。当企业违约时，债权人能通过这种机制接管企业，一般来说，企业资产价值下降会引发违约，从而导致破产，因此破产是企业资产价值下降的结果。使用这种机制的成本就是破产成本，狭义地理解破产成本往往是指企业在清算或重组过程中所发生的法律费用支出，然而广义地理解破产成本可能指财务危机的成本。正如本书在1.2.3中指出，破产成本往往是影响企业资本结构决策的重要因素，实际上，破产成本直接影响的是企业所发债务的价值，破产成本越大，债务价值越低，从而债权人会要求更高的风险费，增加了企业债务融资的成本，从而决定企业的资本结构。因此，研究资本结构不能不研究企业债务估值，而研究企业债务估值不能不研究企业破产成本。

破产成本往往是企业违约由企业支付的费用，实际上由债权人支付。由于一旦企业违约，债权人将取得企业资产的所有权，破产成本的支出，减少了企业资产价值，从而降低了债权人所可能获得的补偿。实证研究发现，破产成本往往占企业违约时资产市值的很大比例，White（1983）、Altman（1984）、Weiss（1990）的研究发现，企业破产的直接成本大约是企业市值的3%，一些小企业的破产成本占企业市值的更大份额，可能达到30%，因而在破产过程中也存在规模效益。然而，如果考虑破产的间接成本，Altman估计破产的直接成本、间接成本之和会远远大于企业价值的20%。^[10]与国外相比，我国企业破产的各种成本（不仅包括法律费用）可能更高，中国工商银行企业破产问题课题组对实行“资本结构优化”试点的50个城市的企业破产问题做了专门调查，调查显示，转轨时期企业破产后债权人的利益难以得到保障，利用破产形式逃债废债较为普遍，据工商银行的统计，企业破产后，该行破产企业贷款的受偿率仅为15%左右，说明破产成本（直接成本与间接成本）远远高于国外的实证结果。^[11]

破产成本是一种不容忽视的流向第三方的支出，破产成本的存在，将使MM定理难以成立。如果仅有破产风险而无相应成本支出，Merton （1974，1977）证明了MM定理仍能成立。正是由于默顿、布莱克等人未考虑破产成本，使得他们的结果与实际金融市场数据不太吻合。当然，引入破产成本后，对于贴现债券，难以找到解析解，实际上Merton的分析仍是可用的，关键是边界条件会发生变化。

设在破产点，企业资产价值为VB，先假定VB是外生给定的（在3.3我们将放宽这一限制，考虑最优资本结构），由于有破产成本，债权人在企业破产时只能得到g（VB），这里g（VB）＜ VB，VB- g（VB）即为破产成本，其既可以理解为破产过程的直接成本，也可理解为包含各种破产间接成本，如无形资产、声誉等的丧失，另外也可能包括重组时股东获得的一部分。g（VB）可以取线性函数，也可以取非线性函数。为反映规模效益，随着VB增加，g（VB）/VB也变大，即债权人得到保障的比例随企业破产资产价值的规模而变化。一旦企业资产价值达到VB，即触发破产，因此对于风险贴息债，企业债务价值F（V，t）仍满足式（3.8），即：

但边界条件发生变化，边界条件为：

这个偏微分方程一般没有解析解，由于企业价值在到达0之前就会引发破产，因此边界条件（3.9.a）不起作用，我们换成（3.9.a′）说明当V充分大时，债务无风险。而把初始条件（3.9.c）换成（3.9.c′），这时就不能利用B-S公式先求f（V，t）值，再求F（V，t）。实际上这里只能利用数值积分技术（Numerical Integration Techniques）（Merton，1974）。为了更好地理解破产成本VB- g（VB）对债务价值的影响，我们可以考虑另一种债务，即永久性息票债务。Mella-Barnal ＆ Perraudin（1993）曾考虑过永久性债务，另外Merton（1974），Black ＆ Cox（1976）也均注意到永久性债务估值可得到解析解（未考虑破产成本）。不失一般性，我们假设每单位时间的连续性利息支付为C，并设每单位时间的连续性股利支付为dV，即比例于企业资产价值，利息支付是由企业发行新股权融资来支付，但假定企业可以出售资产来支付股利或由资产的增值来支付股利，因此，只有当股权价值为0时，企业才难以用新股权融资，这时企业违约或破产。因而永久性息票债务价值F（V，t）满足的方程如下：

其边界条件如下：

注意到式（3.14）中不含Ft或Fτ，事实上，由于考虑的是永久性债务，Ft（V，t）= 0，即认为F（V，t）不显含t，即F（V，t）=F（V），这与Black ＆ Cox（1976）中的式（3.13）是一致的（我们这里考虑了股利支付与破产成本，而在他们的文章中，这两点均未考虑）。

由于（3.14）是一个二阶常微分方程，其有通解如下：

其中：

X、Y分别是（3.14）的特征方程的两个根的相反数，利用边界条件（3.15a）不难得出：

而利用边界条件（3.15b），可计算出：

因此：

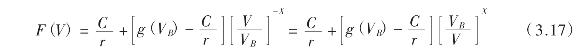
实际上，方程（3.17）可改写成如下形式：

其中：可看做是将来破产的可能性或相机于将来的破产1元的现值，由于通过式（3.17），我们可看出永久性债务价值F（V）与破产成本的关系，对于同样的VB，如破产成本越大，g（VB）会越小，从而F（V）值越低，反之，债务价值越高。另外，我们也可看出破产点对债务价值的影响，即破产点资产价值越高，VB越大，g（VB）一般也会越大，然而会越大，因此对债务价值的影响是不确定的。从债权人的角度来看，设置较高的破产点，既有好处，也有坏处，好处在于一旦企业破产可以获得更多的补偿，而坏处在于破产点设置越高，越有可能发生破产，由于存在破产成本，债权人的利益会立即受到损害。这改进了Black ＆ Cox的结论。

而从式（3.18）可以看出，决定PB的变量主要有VB/V，r，d，σ2。其中VB/ V类似于Black ＆ Cox（1976）给出的公式即式（3.13）中的y，只不过y的分子是重组边界，而这里VB为破产边界。显然VB/V越大，X不变时，PB越大，特别地，当我们把VB看做与负债相关的变量，如是息票C的函数，则VB/V表示一种“准”负债比率，因此，负债比率越高，破产的可能性会越大，与人们的直觉是一致的。

而由X的表达式，不难发现，X随r增加而增加，随d增加而减小，随σ2增加而减小。当我们固定VB /V时，由于VB /V≤1而X＞0，PB = （VB /V）X随X增加而减小，随X减小而增加。因此PB随r增加而减小，随d增加而增加，随σ2增加而增加，这也与我们的直觉一致。^[12]

股利支付越多，企业经营风险越大，企业更可能破产，联系到式（3.17）或（3.18），企业债务价值更低，然而无论σ2，d如何大，企业债务价值都有一个地板价即下界g（VB），F（V）≥g（VB），因此破产点VB的设定可看做是Black ＆ Cox（1976）所提到的安全条款（Safety Covenants）。

由式（3.17），我们还可计算公司永久性债务的收益率及收益利差（Yield Spread），收益率用R表示，利差用R - r表示，则：

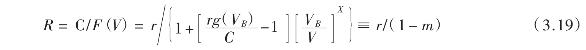
由于分母必然小于1，故R＞r，而R - r即风险费有如下表达式：

其中：

由于C - rg（VB）可看做是一旦企业破产，债权人的单位时间损失，PB表示破产可能性，故m可看做是债权人，可能面临的由企业破产而导致的损失比率，而风险费R- r可看做是债权人因面临破产可能导致的损失而获得的补偿。我们给出的风险费的含义不仅包括Merton（1974）、Black ＆ Cox（1976）的风险费中包括的破产风险，而且还包含由破产而可能导致的破产成本损失，因此，这里给出的风险费的含义更广泛，更贴近现实情况。另外，由式（3.19）可看出，由于1- m表示未受损失部分，因此债务价值收益率R用未受损失部分应达到无风险利率r来表示。

在我们给出的公式（3.18）、（3.19）、（3.20）中，VB，g（VB），V，r，d，σ2大多数是可观测变量，实际上VB外生给定，g（VB）可以通过不同行业、不同规模内破产企业数据统计得到，特别需要确定g（VB）的函数形式，r可由长期国债利率代替，d可根据历史数据或同类企业数据计算。只有σ2相对难以确定，根据Jones, Mason and Rosenfeld（1984）所做的实证工作，他们用两种方法估计σ2，一种方法是利用企业资产价值的时间序列数据，计算企业资产价值的回报及回报标准差，而企业资产价值数据他们是运用股权市值、交易债务市值以及非交易债务的估计市值求和计算得出。另一种方法是利用方程（3.4b），不过把r看成是股权证券，用股权证券的标准差来计算，即用：

要想得到σ，只须统计出σE，并估计出弹性系数VEV/ E即可。因此，我们能够容易地利用（3.18）、（3.19）、（3.20）分别计算出不同企业的债务价值、债务收益率及收益利差。

当然，我们这里给出的仅仅是永久性债务估值，对于包含破产成本的有限期公司债，正如在对式（3.8）、式（3.9）中所讨论的，可以通过现代计算技术如马尔科夫链（Markov Chains）法或有限差分（Finite Difference）法来逼近解。^[13]实际上，当到期时间T充分大时，正如Brennan ＆ Schwartz （1978）所做的实证分析显示，如T超过25年，债务价值对T就不敏感了，因此这里给出永久性债务价值可以看做是长期息票债务价值的一个好的逼近。事实上，对于30年期债务，如果利率是15%，则到期支付的本金仅占债务价值的1.5%，而如果利率是10%，则到期支付的本金也仅占债务价值的5.7%。这时本金的偿还就意义不大或可以忽略不计。

比较我们的结果与默顿、布莱克等人的工作，我们发现我们给出的公式有更明确的经济含义，也可以看做是布莱克等人工作的推广。默顿（Merton, 1974）在考察有限期息票债务时，发现难以得到闭式解或解析解，但他发现，当T→∞，即永久性债务时，可以得到如下表达式：

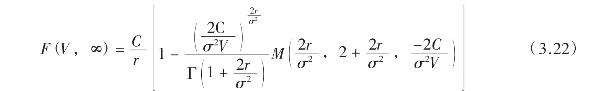
其中Γ（　）是gamma函数，而M（　）是合流型超几何函数（Confluent Hpergeometric function），当然，默顿未考虑股利支付及破产成本。默顿认为公式（3.22）可作为优先股的定价公式。我们的结果更贴近布莱克等人（Black ＆ Cox，1976）的工作，在不考虑股利支付与破产成本，且重组边界给定为时，他们给出永久性债务价值F（V）的如下表达式：

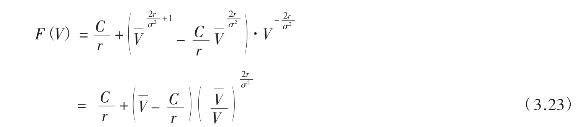
因此，我们的结果式（3.17）可看做是布莱克等人结果式（3.23）在包含破产成本与股利支付下的直接拓广。

由于我们考虑了破产成本，因此，我们能把资本结构与公司债务价值连在一起，公式（3.17）可看成资本结构对公司债务价值的影响，而反过来公司债务价值也会对公司选择资本结构有很大影响，具体将体现在VB的确定上，如果VB是由企业或股东确定而不是外生给定，债务价值又如何影响公司资本结构决策，这是我们3.3节的任务，在此之前，我们利用这里给出的公式，探讨纯混合兼并对公司债务价值的影响。

3.2.3　纯混合兼并对风险债务价值的影响分析

资本运营作为企业的高级经营战略，正日益受到我国企业界的关注，兼并作为资本运营的核心之一更是其中的热点。混合兼并是兼并的一种，西方曾出现过混合兼并浪潮，我国目前也有大量兼并案例，但混合兼并相对较少。能否通过混合兼并改善企业的债务状况，是一个值得研究的问题，由于企业大多处在不确定环境下，可以运用相机权益分析方法，探讨纯混合兼并对企业债务价值的影响。

企业兼并大致可分为三类：第一类是水平兼并或横向兼并，双方生产同类产品；第二类是垂直兼并或纵向兼并，被兼并公司成为兼并公司的供应者或消费者；第三类即混合兼并，指兼并与自身产品不相关的企业。一般来说，横向兼并能带来规模效益，提高市场占有率；垂直兼并可使交易内部化，降低交易成本，防止敲竹杠（Hold-up）；混合兼并能带来什么经济利益呢？这里，我们把混合兼并分为三种类型，即产品扩展型、地域扩展型及纯混合兼并，其中纯混合兼并的经济合理性最弱。虽然也有一些经济学家考虑混合兼并的协同作用，认为混合兼并形成的大企业可以更有效地利用高级管理技术，降低经营成本，即2+ 2＞ 4。然而纯混合兼并并不考虑协同作用，我们把不具有协同作用，而单纯考虑混合兼并财务效应的兼并称之为纯混合兼并，即2+ 2= 4。纯混合兼并重点探讨混合兼并对股权价值的影响，早期的研究主要从期权定价模型（OPM）出发，把股权看做企业资产的一种看涨期权，只要知道债务到期日、面值及无风险利率，就可运用一定的公式，求出混合兼并后股权的价值，这里一般不需考虑债务价值。然而这种方法并未考虑破产成本，在有破产成本情形下，混合兼并对债务价值的影响就需要考虑。

我们首先考察一家企业，这家公司仅发行两种证券，即股票和永久性公司债。所谓永久性公司债是指债务的期限是无限长的，但每期支付利息。事实上，永久性公司债无论是理论上还是实践中均不是新的。理论研究中，莫迪利亚尼和米勒在他们著名的MM定理中就假定公司债是永久性的，布莱克等人（Black ＆ Cox，1976）也作了类似的假定，但他们未考虑破产成本；而实务中，英格兰银行早在1751年就发行无到期日的统一公债（Consols），优先股也类似于永久性债务。另外，由于贴现因子的作用，长期债务也可近似看做永久性债务。

永久性债务的价值依赖于企业资产的价值V，企业资产的价值高，就会有更多资金支付债务利息，企业就不会违约。按照默顿的观点，由于企业资产价值V本身是一随机变量，其大小依赖于将来的状态，当债务价值是资产价值V的函数时，事实上债务价值是一种相机权益（Contingent Claim）。由于企业处于一个不确定的环境内，企业资产价值会随时波动，我们假定企业资产的价值V服从如下扩散过程：

其中μ（V，t）是企业资产的瞬时预期增长率，σ是瞬时波动率，Wt是标准Brown运动。

企业资产可能向上波动，也可能向下波动，因此，企业资产可能向上波动，也可能向下波动，因此，企业债务可能面临违约的风险。公司债务价值记为F（V，t），不妨设F（V，t）关于V，t二阶连续可微，每单位时间支付利息为C，C≥0（这里不妨设连续支付利息）。同时假定无风险资产的收益率为r，r不随时间变化，即不考虑期限结构。这里不隐含一个假定，即公司债务利息支付是通过出售股权进行的。

下面，我们导出F（V，t）关于V，t的表达式：^[14]

由Ito引理，对F（V，t）微分，可得：

其中：把式（3.24）代入式（3.25），得到：

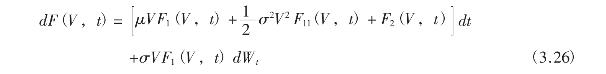
考虑这样一种证券组合：

-1：公司债F（V，t）

+ F1（V，t）：公司资产V

此证券组合的持有者卖出一份公司债，买入数量为+ F1（V，t）单位的公司资产（这里假定公司资产与公司债均可交易，实际上这不是必要的）。定义证券组合的价值为∏，并设Δ∏，ΔF，ΔV分别是时间Δt内∏，F（V，t）V的变化，则：

把式（3.24）和（3.26）的离散形式代入式（3.28）右端，则有：

在时间Δt内，持有该证券组合的投资者，获得资本利得Δ∏，但由于公司债支付连续利息，失去利息收入为CΔt，故其在Δt内收益为：

由于Δ∏- CΔt是无风险的，由无套利条件，得到：

又由式（3.27），得到：

这是一个偏微分方程，一般不具有解析解，但我们这里考虑的是永久性债务，可认为永久性债务价值F（V，t）与t无显性关系，即F（V，t）= F（V），故Ft（V，t）= 0，因而式（3.32）变为：

这就是F（V）必须满足的二阶常微分方程，其有通解：

其中：

而常数A0，A1，A2由边界条件确定，下面我们考虑边界条件。

对于企业债务，只要经营好，债务就无风险，则债务价值为息票支付之和，为，因此一个边界条件是：

当V→∞时，F（V）

然而企业有可能破产，设VB为公司宣告破产时资产的价值，并假定破产成本比例于VB，为βVB，其中0＜β＜1，为破产成本系数。由于有限责任，破产时债权人只能得到g（VB）=（1 -β）VB，股权价值为0。^[15]因此，另一个边界条件为：

当V = VB时，F（V）=（1 -β）VB

由上述两边界条件，可解出：

代入通解，可得到：

由于式（3.35）右端第二项小于0，故F（V）＜C/r，事实上，式（3.35）可写成：

其中：为破产概率，当α确定时，VB越大，破产的可能性越大。特别当VB表示为企业的债务面值或债务面值的比例时，可表示为准资产负债率，因此，由式（3.36）可看出，资产负债率的高低直接影响公司债务价值。另外，由，因此企业资产价值的波动也直接与破产概率有关，波动越大，即σ越大，由于VB≤V，则PB越大，从而F（V）越小。还可看出破产成本系数β对F（V）的影响。

现考察两个公司，不妨设为公司1、公司2，它们的资产价值均服从类似于式（3.24）的方程，并假定都受到同一个基本的不确定来源（如宏观大环境）的影响，但参数值不同，分别为：

两家公司均发行永久性公司债（这可避免债务期限不同引起的复杂性），息票支付分别为C1，C2，其债务价值分别记为F1（V1），F2（V2），则类似于式（3.35），推导可得：

VB1，VB2分别为公司1、公司2破产时资产价值，破产成本系数均为β。则两公司债务价值之和为：

现两家公司混合兼并，不考虑协同作用，则合并后公司资产价值V= V1+V2，则由Ito引理[见（Hull，1977）附录12.A]则V也服从类似的扩散过程：^[16]

由于合并后企业资产回报率的瞬时波动可看做是公司1、公司2资产回报率瞬时波动的加权平均。

立即有：

由于混合兼并后，利息支付为C1+ C2，破产点资产价值VB=VB1+VB2，破产成本系数不变，则类似于（3.35）式的推导，混合兼并后公司的债务价值F（V）为：

由式（3.44）与（3.45）可直观看出混合兼并后，破产概率有可能变化，如破产概率不变，即PB= PB1= PB2，则两公司债务价值均不发生变化，总债务价值也不发生变化，此时混合兼并对各公司的债务价值无任何改善，只要混合兼并后的破产概率与兼并前不等，则一定有公司债务价值发生变化，下面是我们的主要结论：(www.xing528.com)

1.当VB1，VB2为债务面值时，该式说明兼并时两公司资产负债率相等，有此时α决定了各公司债务价值的变化，大致有以下两种情况：

①σ1=σ2，则σ=σ1=σ2，此时PB = PB1= PB2，比较式（3.39）、（3.40）、（3.45），可看出，各公司债务价值均不发生变化，且F（V）= F1（V1）+ F2（V2）。

②σ1＜σ2，则σ1＜σ＜σ2，此时PB1＜PB＜PB2，则公司1的破产可能性在兼并后上升，公司2的破产可能性在兼并后下降，因而混合兼并后，公司1的债务价值下降，而公司2的债务价值上升，即在资产负债率大致相当时（VB表示为债务面值），资产价值波动大的公司经过混合兼并，可改善其债务状况。

2.，即兼并时公司1的资产负债率低于公司2的资产负债率时，有即混合兼并后资产负债率比公司1高，比公司2低，可考虑下列三种情况：

①σ1=σ2，则σ=σ1=σ2，此时PB= PB1= PB2，则混合兼并后，公司1的债务价值下降，而公司2的债务价值上升，即当各公司资产波动率大致相当时，资产负债率高的公司通过混合兼并可改善其债务状况。

②σ1＜σ2，则σ1＜σ＜σ2，此时仍有PB1＜PB＜PB2，说明资产负债率高，且资产价值波动率大的公司通过混合兼并可改善其债务状况。

③σ1＞σ2，则σ2＜σ＜σ1，此时必须有相应数据才可判断各公司的债务价值变化方向。

3.3　不确定环境下的最优资本结构研究

企业债务价值对资本结构的影响在于债权人能理性预期到企业债务所面临的风险，即使债权人在债务人违约时能取得相应补偿，但由于有破产成本，债权人将得不到足够补偿，因此债务人在发行债务时必须提供更高的承诺息票，才能获得债务资本。正如平衡理论所指出的（见1.3.2），获得债务资本的好处在于债务利息是免税的，两者的权衡可以得到最优资本结构。这一节我们将在不确定环境下探讨最优资本结构的决定要素，特别地，正如我们能给出企业债务估值公式一样，我们也可给出破产成本与免税现值的数学表达式，从而能定量给出最优资本结构。

经常所讨论的不确定环境是两方面的。一方面，正如前面讨论所假定的，企业资产价值具有不确定性，并且这种不确定是外生的，由一个随机微分方程来描述，其合理性已得到默顿、布莱克及其他许多金融经济学家的论证，从而存在于大量金融经济学文献之中。另一方面，正如常常假定股票价格具有几何布朗运动一样，也可以假定企业产品价格也具有类似的运动轨迹，或者更严格地说，假定企业的销售收入服从几何布朗运动。这样假定的好处在于能够发现资本结构与产品价格或企业销售收入之间的关系，他们与我们讨论的共同点均在有破产成本与免税效应前提下，通过企业债务价值估值，决定最优资本结构。^[17]因此，通过企业资产价值的不确定性对债务价值的影响，进而影响到最优资本结构的决定是本节的出发点。

3.3.1　不确定企业资产价值与企业总价值

我们这里完全延续3.2.1与3.2.2的假定，并且式（3.17）或式（3.18）仍成立，即企业债务价值由V，VB，r，d，σ2等确定。我们前面假定VB是外生设定的，这里我们将讨论VB内生对资本结构的影响。

我们考虑内生破产的情形，所谓内生破产是指当企业不能通过新的股权融资来满足息票支付时，则破产被引发，企业不受债务契约条款的限制，自己决定何时停止向企业注资，即股权价值为0（否则向企业注资总是有利的）。当然，如果企业没有足够的现金来支付息票，即资金短缺也可能引发破产，但是只要股权价值为正，企业总可进行另外的股权融资来解决资金短缺而不是宣布破产。正如在3.2.2中式（3.17）看出，VB会影响债务价值F（V），从而也会影响资本结构。债务会从两方面影响企业价值（注意这里不是企业资产价值V或完全股权企业价值）。一方面，由于财务危机（或可能的破产）所引发的成本降低了企业价值（虽然其对企业资产价值无影响），另一方面，由于税收对债务利息支付的优惠，负债能增加企业价值。然而这两方面均与破产点VB有关。

从金融学角度出发，只要企业支付债务息票，假定某种证券支付常数利息等于债务息票支付的税盾（Tax-sheltering）价值即τC，其中τ表示公司所得税（除此税种外，本书不考虑其他税种，如个人所得税、股利所得税等），但是一旦企业不支付息票（即企业破产），这种证券支付为0。这种虚拟的证券价值实际上就是债务的免税现值。显然，其依赖于企业资产价值V，如当V充分大时，即企业不可能违约时，税盾始终是可以得到的，则现值为τC/r，而当V不足以支付息票时（即股东停止向企业注资）则税盾为0，因此，也是一种相机权益（Contingent Claim）。现令TB（V）表示债务的免税现值，则我们得到两个边界条件：

由于V具有不确定性，服从如下随机微分方程：

而TB（V）与时间t独立，因此TB（V）满足如下微分方程：

由式（3.48）加上两个边界条件（3.46），则与式（3.17）一样可得：

其中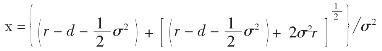：，同样，TB（V）也可写成：

其中：表示破产可能性。由于VB越大，PB越大，从而TB（V）越小，因此，从股东的角度，为了最大限度地获取免税现值，将尽可能使VB变小。

同样，可以考虑财务危机的成本现值，财务危机的成本只有在破产发生时才会发生，我们这里就考虑各种破产成本。设破产成本的现值为BC（V），其也是一种相机权益（Contingent Claims），则类似于TB（C），BC（V）满足如下微分方程：

边界条件为：

则可解出：

或写成：

由式（3.53）或（3.54）可看出，破产点VB设置越高，PB越大，而＜1，VB- g（VB）即破产成本支出也会越大，综合起来破产成本现值BC（V）就越大。因此，从降低破产成本角度出发，VB应越小越好。固定VB，由PB的表达式可知，资产价值V越大，PB越小，从而BC（V）越小，d，σ2的增大或r减小，都会使BC（V）变大。

根据资本结构的平衡理论，即式（2.2）或2.3.2提到的调整现值法（APV），企业总价值T（V）可表示为三项的代数和，即企业资产价值V，加上息票支付的免税现值，减去破产成本现值，因此把（3.49）与（3.53）代入可得：

然而，根据式（3.55）我们不能求出最优资本结构，实际上，由于C，VB/V均可能与资本结构有关，特别是VB值尚不确定，因此最优资本结构须待VB内生确定后再讨论。

为简单起见，定义企业债务价值与股权价值分别为D（V）与E（V），则

把T（V）的表达式（3.55）及D（V）的表达式（3.17）代入，可得：

股东关心的是股权价值E（V），而不是企业价值T（V），从（3.55）式可看出，要使得T（V）达到最大，应尽量使PB达到最小（因为VB＞g（VB））。然而从式（3.57）中可看出，当时，增加PB会增加股权价值E（V）的值，这就是一种债务代理成本，虽然PB增加降低了企业价值，但却增加了股权价值，显然，财富从债权人流向债务人。正如我们在前面讨论的，d，σ2增加，都会导致PB的增加，而d由企业的股利政策决定，σ2由企业的投资政策决定，因此，股东可以从股利政策与投资政策两方面来进行“资产替代”，产生如1.3.3所涉及的“资产替代效应”。企业在财务危机时发放更多的股利或投资在风险更大的项目等自私策略（见1.2.3）在时恰恰相反，也会减少股权价值，但是正如我们下面要给出的，内生破产点这给了债务人进行资产替代的机会。这也说明公式（3.57）能较好地说明资产替代问题。

3.3.2　内生破产点的确定

为了得到内生破产点VB，必须从股东角度出发，只要股东停止向企业注资支付债务利息，企业就引发破产，因此股东将会阻止VB任意小（从而破产可能性更小），而使股权价值为非负。实际上，股东选择VB要使得股权价值E（V）在任何一个V值均能达到最大，即任何一个V，都有dE/dVB = 0，如同Samuelson（1965），Merton（1973b）给出的“High Contact”条件一样，这里等价地给出“Low Contact”条件，^[18]即dE/dV|V=VB= 0，也是股东决定最佳内生破产点条件，由于两个条件等价，我们只需利用其一，并注意到X是方程的负根的相反数，就可得到VB的表达式：

显然，E（V）是V的增函数，即dE（V）/dV＞0，且是V的凸函数，事实上，把式（3.58）代入式（3.57），并对V求导，则立即有：

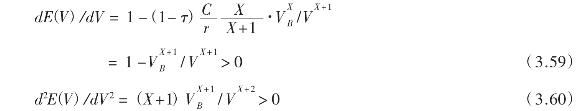
由式（3.58）可以看出，决定内生破产点VB的因素主要有公司所得税税率τ，债务利息C，以及r，X。分析式（3.58）可知，首先，VB与债务利息C成正比，实际上，其与债务无风险值成正比。其次，VB随公司税率τ上升而下降，随d增加而减少，随σ2增加而减少，但r对VB的影响是不确定的。再次，VB与现在企业资产价值V无关，也与破产后债权人能够获得的g（VB）的函数g无关。因此，决定企业的内生破产点VB的不是企业现有多少资产，而是与这些资产相匹配的负债，资产经营的风险以及企业实行的股利政策。

把式（3.58）代入到式（3.17）、（3.55）及（3.57），可以得到D（V），T（V）及E（V）的表达式，为更清楚地说明问题，以下我们取g（VB）= （1-α）VB- k，对应于VB-g（VB）=αVB+ k，其中k为大于等于0的常数，即破产的固定成本，而αVB为破产的可变成本，这里设为线性函数，其他函数可类似讨论。这里给出的假设也符合破产中的规模效益，即资产价值越大，破产成本支出占资产值的比例越小，这是由于有k＞0，从而可大致体现这种情况。D（V），T（V），E（V）的表达式如下：

其中：

把内生破产点VB取值代入式（3.19）与式（3.20），则可得公司债收益率及收益利差，实际上形式不变，只是m的取值发生变化，即：

其中：

由于公司税率τ影响内生破产点VB，从而影响D（V），E（V），T（V）价值。虽然破产成本支出（无论是固定破产成本k，还是可变破产成本αVB）不仅影响债务价值D（V），而且影响企业总价值T（V），但却不影响股权价值E（V）。

综合上述结果，我们给出如下命题：

命题1：假设企业资产价值是外生的且由方程式（3.47）决定的随机过程给出，债务利息支付固定为C，并且破产成本VB- g（VB）=α（VB）+ k，则企业债务价值D（V）、总价值T（V）、股权价值E（V）分别由式（3.61）、（3.62）、（3.63）确定，并且内生破产点VB由式（3.58）确定，收益率R及收益利差R - r由式（3.64）确定。

由式（3.61）及式（3.62）可以得到负债比率L。

其中：

3.3.3　资本结构的动态调整

前面的结论实际上是在债务利息C固定时得到的，也就是说，一旦企业发行了债务，将一直保持不变。这虽然与现实并不太相符，但我们能够证明，这种假定往往是有道理的。这一部分我们首先来讨论资本结构的调整，即C的变化对债务价值与股权价值的影响，当然企业的经营风险或投资政策不变。利用前面的结论，我们有如下命题：

命题2：假设企业资产价值是外生的且由方程式（3.47）决定的随机过程给出，债务利息C是可调整的，破产成本为VB- g（VB），不考虑可能的补贴，则股权价值持有者（或称股东）将不会赎回企业的债务，即使得C下降。

证明：固定一个水平C，在命题2的假定下，式（3.17）、（3.58）、（3.63）均成立（注意到VB的确定不依赖于函数g的形式），则单位债务须付利息为：

考虑减少一单位债务利息C对股权价值的影响，即坠E（V）/坠C，从而由式（3.63）可得

该式表明减少一单位债务利息C可增加股权价值，下面考虑买回一单位企业债务可能增加的股权价值，则可以用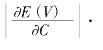来表示，由式（3.66）及（3.67）立即可得：

因此企业发行一单位股权买回一单位债务使得股权价值的增加小于1，股权持有者将会拒绝这种交易。命题得证。

命题2说明，企业投资政策不变，即使在没有信息不对称情形下，增发新股偿还债务也会使股价下跌，因此在1.3.4中所论述的信息不对称并不是增发新股导致股价下跌的唯一原因，在我们给出的模型中，我们能得到类似的结论。另外我们还可得到如下推论，该推论已得到实证检验。

推论1：在定理2的假定下，增发债务回购股份将导致股权价值增加，股东将从回购股份中获利。

证：增发一元债务回购一元股权价值，则剩余股权价值增加一元，但由式（3.67）增发债务将导致股权价值下降，由式（3.68）其下降的幅度小于1-τ，故回购股份，使得剩余股权价值净增加，结论得证。

特别地，如果不考虑公司所得税，即τ= 0，且企业无破产风险，即PB = 0，则容易证明，因此改变负债量对股权价值无影响，与MM定理仍是一致的。

自然能想到的问题是，企业增发债务对原有债权人的利益有无影响，我们的模型同样能回答该问题，下面是我们的结论。

命题3：假设企业资产价值是外生的且由方程式（3.47）决定的随机过程给出，债务利息C是可调整的，破产成本为VB-g（VB），如果g（VB）与g′（VB）均很小，不考虑可能的补贴，则原债权人不会愿意企业发行新的具有同等优先受偿权的债务。

证明：在命题3的假定下，式（3.17）、（3.58）均成立。

设企业因发行新债务导致债务利息增加dC，则债务总价值变化为：

由于债务价值增加由新老债权人持有，新债权人将持有总债务价值dC/C的份额，因此，原有债权人持有的债务价值为：

从而增发新债对原有债权人的影响为dD -（D/C）dC -（dC/C）dD，忽略高阶项，把式（3.69）代入（3.70），并结合式（3.17）与（3.58），而dC＞0，则只须考虑：

只要g（VB）与g′（VB）较小，则：

因此，增加债务发行将使原债权人持有债务价值下降，除非补贴，否则原债权人将不希望企业增发同等优先受偿权的债务。命题得证。

命题3能够解释绝大多数债务合同关于限制增发债务的条款。虽然发行新债务可能增加股权与企业总价值，除非企业发行次级债务，否则原有债权人的利益将受到损失。命题3说明，只要企业破产后的剩余价值很小且其对破产点不敏感，则债权人将会拒绝增加负债。实际上，如令g（VB）=（1-α）VB- k，立即有g′（VB）= 1-α，而则就可由式（3.71）中右端括号内值的正负号决定增发债务对原有债权人的影响。该定理也能够解释次级债务在理论上的存在性，由于优先受偿权利不等，因此不同的债务种类（指优先次序）具有不同的债务价值，^[19]原有债权人必须得到补贴（可能来自股东，也可能来自次级债权人），才会放宽债务合同关于增发新债的限制。更进一步地，正如前面分析，由于PB随σ2增加而增加，而VB随σ2增加而减小，从而公司债务（不考虑优先等级）价值将是σ2的减函数。然而正如Black ＆ Cox （1976）分析的，次级债务价值可能是σ2的增函数，这意味着债权人之间在企业投资政策方面存在利益冲突，即次级债权人会倾向于投资风险更大的项目，而原有债权人则会拒绝这样的项目。因此，在发行次级债务时或在原有债权人债务人达成的合同条款中，一般会赋予原债权人在企业投资决策中比次级债权人更大的权力，以保证原债权人的利益。

3.3.4　最优资本结构的确定

在MM定理之后，基于税赋与破产成本的最优资本结构理论得到了充分挖掘，其中最著名的不外乎在本书1.3.2的平衡理论，债务融资固然能获取债务利息免税优惠，但同时也增加了财务危机的成本，这两部分的权衡被认为决定最优资本结构。我们在不确定的动态环境下，能够给出免税现值与财务危机成本现值的数量表达式，从而能给出最优资本结构的明确表达式。

首先我们来讨论企业的最大债务融资能力，这里企业的“最大债务融资能力”是指，如超过该债务量，则不会有债权人提供资金，因为增加负债，当债务价值开始下降时，将无资金提供者或原债权人会反对。我们可以用表示，^[20]则最大债务融资能力记为C*1，使得：与式（3.67）、（3.69）、（3.71）等符号意义一致，本来D是V，C， r，d，σ2等参数的函数，前面我们主要用D（V）表示D，那是指固定其他变量，把其看成V的函数，而在讨论C的变化对D的影响时，D（V）= D（V，C），故这里用偏导数表示。

式（3.73）说明处的边际债务价值为0。

为简单起见，这里我们令g（VB）=（1 -α）VB，即破产的固定成本k = 0，把式（3.61）代入（3.73）可得：

则得：

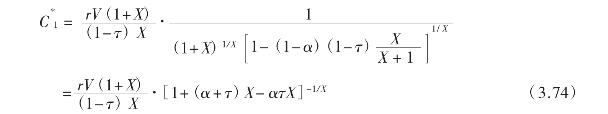
并由，则可知是使D（V）达到最大的债务利息C。结合式（3.58）及，在时，

把式（3.74）与式（3.75）代入式（3.61），并令k = 0，则最大债务融资能力实现时债务价值为：

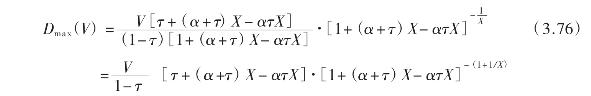
显然，Dmax（V）比例于企业资产价值V，并且由于σ2增加，将导致X下降，PB上升，因此Dmax（V）随σ2增加而下降，即企业经营风险越大，其债务融资能力越差。另外显然破产成本系数α越大，Dmax（V）越小，而由d 与X之间的关系，即X随d增加而减小，因此，债务融资能力也与股利政策有关，即股利支付越多，债务融资能力越差。综合上述结论，有如下命题：

命题4：假定企业资产价值是外生的且由方程式（3.47）决定的随机过程给出，在破产成本为αVB时，则企业的最大债务融资能力Dmax（V）由式（3.76）给出，相应的债务利息与破产概率分别由式（3.74）、（3.75）给出，投资政策与股利政策对最大债务融资能力的影响是经营风险越大或股利支付越多，都会导致Dmax（V）下降。

虽然企业有Dmax（V）这么大的债务融资能力，但是正如Myers（1984）指出的，实际上许多企业特别是有大量增长机会的企业将会充分保留其债务融资能力，以备将来有更好的投资机会时再融资，因此一般达不到Dmax（V）。另外，注意到仅是使得D（V）达到最大，仅仅是从债权人愿意出资的角度，因为超过，则D（V）开始下降，债权人是不可能出资的，实际上债权人、债务人均希望的最佳负债量是使得企业总价值T（V）达到最大，相对应的最佳债务利息记为，使得：

对于破产成本，同样有V- g（VB）=αVB，则由式（3.62）可得：

由式（3.77）并注意到如τ= 0，则 = 0，因此设τ＞0，有：

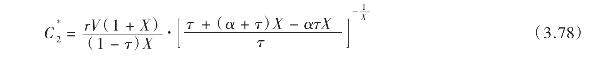
其中h≡τ+（α+τ）X -ατX，显然h＞0，从而有坠2T（V）/坠C2＜0，因此是使得T（V）达到最大的最佳债务利息。

如同式（3.75）一样，在时有：

比较PB1与PB2，可以发现PB1＞ PB2，从而立即有把式（3.78）、（3.79）及k = 0代入D（V），T（V）的表达式（3.61）、（3.62），可以得到最佳债务量D*（V）、最大企业总价值T*（V）及最优负债比率L*。

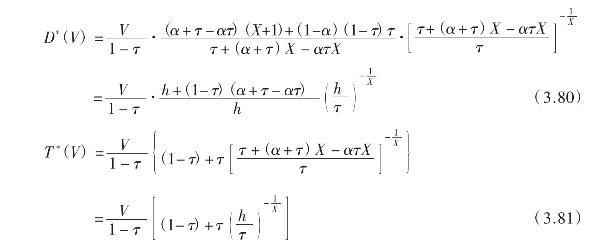
则由式（3.65）对L的定义，立即有：

显然L*与V无关，由于X由变量d，σ2，r决定，故L*可写成：

即最优资本结构由企业的股利政策、经营风险（或投资政策）、破产成本、所得税税率及无风险利率决定。综上所述，我们有如下结论：

命题5：在命题4的假定下，企业的最优资本结构（负债比率）L*与企业资产价值V无关，且由式（3.82）决定，企业的股利政策、投资政策、破产成本、所得税税率及无风险利率共同决定了最优资本结构。相应地最优债务量D*（V）及企业最大总价值T*（V）分别由式（3.80）与（3.81）决定。而最优债务利息与破产概率分别由式（3.78）与（3.79）决定。

推论2：在命题5的假设下，企业最优资本结构对应的债务收益率及收益利差分别为：

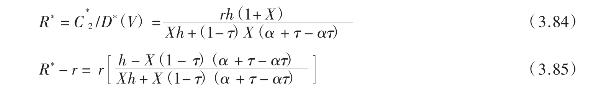
证明：由命题5的结论，由式（3.78）给出，C*（V）由式（3.80）给出，代入R的定义及R - r的定义，立即有式（3.84）与式（3.85）。证毕。

下面我们通过模拟数据给出最优资本结构与各因素变量之间的比较静态分析结果。见表3.1及表3.2。

根据计算的结果，可以看出企业的投资政策（企业经营风险）、股利政策（股利支付）、资产流动类型（破产成本）对最优资本结构的影响。而且也能分析出不同政策的相互作用对资本结构的影响。

首先，固定其他变量，可看出企业经营风险对资本结构的影响主要体现在企业经营风险σ2越大，PB2越大，最优资本结构（负债比率L*）越小，收益率R*越大，反之，企业经营风险σ2越小，PB2越小，最优负债比率L*越大，收益率R*越小。特别地，当σ2＞ 20%，而d ＞ 1%时，破产可能性将达到98%以上，最优负债比率在50%左右，收益率R*异常放大，达到300%以上，说明债务价值已远远低于票面价值。而当σ2＜1%，而d = 0时，破产可能性几乎为0，最优负债比率可达到90%以上，收益率R*将与无风险利率r一致，如σ2= 0.5%，d = 0，则X = 20，PB2 = 3%，L*= 91.83%，R*= 5.07%。注意到当σ2=20%时，如d = 0，则债务仍较为安全。

表3.1　最优资本结构与企业特征变量之间的关系

其次，固定其他变量，股利支付对最优资本结构也有显著影响，可以看出，随着股利支付的增加，PB2上升，而最优负债比率下降，债务收益率上升。特别地，当企业经营风险较小时，股利支付增大对最优资本结构的影响相对较小，如σ2= 0.01时，股利支付增加0.01，最优负债比率大约下降2%左右，而当σ2=0.04时，最优负债比率大约下降7%左右，当然，当最优负债比率靠近58%左右时，股利支付的增加其影响很小，因为此时破产可能性已高达90%以上。特别有趣的是不支付股利与支付股利对破产概率、最优负债比率及债务收益率的影响有很大差异，实际上，即使σ2= 0.3，而d = 0时，债务仍然相对较为安全。

再次，由于股利支付与企业经营风险决定了变量X，而PB2，L*，R*也直接与X有关，因此，我们可以看出股利支付策略与企业投资策略的相互作用。由表3.1（a）可以看出，X = 1对应的（σ2，d）的组合共有三对，即（0.01，0.04），（0.04，0.01）及（0.10，0.00），说明即使企业经营风险增加，但股利支付相应下降，或企业经营风险下降而股利支付增加对最优资本结构的影响将相互抵消，从而能在这两种政策之间进行选择。

最后，破产成本对资本结构的影响由表3.1（b）给出，固定X（即投资政策与股利政策固定，或相应调整），可看出，破产成本系数α越大，最优负债比率越小，这说明破产后企业资产的流动性或重组后企业资产的生产能力对资本结构的影响，即企业资产类型（如有形资产与无形资产）对企业债务融资影响的定量刻画。然而，令人惊讶的是破产成本系数α越大，破产概率与债务收益率反而越低，这是因为当固定X时，最优负债比率越低，破产可能性越小，从而债务收益率也越低。特别地，当X取值较大时，如X = 7，则破产成本系数对最优负债比率的影响较小，成本系数由0.7降至0.1，最优负债比率增加约12%，对破产概率与债务收益率R*影响也很小，但当X取值较小时，如X=1或X = 0.041，则破产成本系数对最优负债比率、破产概率及债务收益率R*的影响要大得多，如X = 0.041时，成本系数由0.7降至0.1时，最优负债比率增加约60%。因此当企业经营风险与股利政策不利于债权人时，破产成本就显得更为重要，而当企业经营风险很小时，破产成本对资本结构的影响也很小，这说明破产成本对资本结构的影响还须依赖企业经营风险与股利政策。

同样，我们可以考虑企业外部环境变化如企业所得税税率、无风险利率变化对资本结构的影响，见表3.2。

表3.2　最优资本结构与公司所得税税率及无风险利率的关系^[21]

其一，企业所得税税率由33%降至15%会对企业的破产概率PB2，最优负债比率L*以及债务收益率R*产生显著影响，在X = 7或X = 1，α= 0.7时，τ由33%降至15%时，PB2约下降一半，最优负债比率L*在X = 7时降约12%，而X = 1时下降约22%，说明企业所得税税率的变化对风险更大的企业的最优负债比率影响更大。而在α= 0.3时，τ的变化对PB2的影响要小于α= 0.7时，PB2约下降至原先的30%～40%之间，虽然企业所得税税率的变化也对风险更大的企业的最优负债比率影响更大，但影响力度比α = 0.7时要小，如在X = 7时，α= 0.3，最优负债比率下降约9%，而在X = 1，α= 0.3时，虽然最优负债比率也下降约23%，但其下降幅度仅为原来68.90%的35%左右，同X = 7，α=0.3时税率变化导致最优负债比率下降幅度为原来的50%左右有一定差距。所得税税率对债务收益率R*的影响依赖于r的取值，明显的所得税税率的下降将导致债务收益率R*的下降，但在r取同样值时，X取值越小，所得税税率对R*的影响越大。

其二，从表3.2中可以看出，在固定X，α，τ值时，r的变化对PB2与L*无影响，实际上这也可从式（3.79）、（3.82）中不显含r可看出，r的变化对R*的影响也仅是比率变化，还可以从（3.84）中看出。然而正如我们在表3.2的下注中指出的，实际上X与r有关，在给定σ2，d时r的增加将导致X增加，而当X固定时，r的增加必将导致σ2，d的相应增加，X才不变，从而不影响最优负债比率。因此可以说，在企业投资政策与股利政策固定时，经济形势好转（如快速增长）将使得企业的最优负债比率增加（因为X增加），换句话说，在经济膨胀期，即使企业的经营风险很大，企业也可以债务融资，或对于所有企业，大多可以增加债务融资，提高负债比率。这个结论与1.2.4中介绍的Lamont（1995）或Shleifer ＆ Vishny （1992）的观点一致。

其三，综合表3.1与表3.2，我们可以发现最优负债比率在50%以下的企业内部特征与外部特征。在表3.1（a）中，即使企业经营风险很大，如σ2达到0.20，在α= 0.3及τ= 0.33时，最优负债比率仍在50%以上，但改变α取值或改变τ取值，情况就会发生变化，如在表3.1（b）中，X = 1，α= 0.7，τ= 0.33时，最优负债比率为46.24%，而当α下降为0.5时，即破产成本是剩余资产价值的一半，则最优负债比率又上升到50%以上。当破产成本与经营风险均很高时，如X= 0.041，α= 0.7或0.5，其最优负债比率均在50%以下，甚至仅20%左右。同样，在表3.2中，我们发现，即使X = 1（按照表3.2的下注的说法，对应的是低风险、高股利或高风险、低股利的企业），当破产成本很高（α= 0.7）时无论所得税税率为33%还是15%，最优负债比率也在50%以下。特别地，当所得税税率为15%时，最优负债比率也仅20%左右。当所得税税率为15%时，即使破产成本系数α= 0.3，最优负债比率也在50%以下，更进一步地，我们能够发现，破产成本系数与所得税税率同时从高位（α= 0.7，τ= 0.33）降至低位（α= 0.3，τ= 0.15），最优负债比率几乎不发生变化。

最后一点的发现有助于我们解释高科技企业为何一般很少有负债，从而必须要有风险投资基金支持。高科技企业的内部特征是σ2和α很大，而τ很小，因此，其必然具有很低的负债比率，甚至完全没有负债。高科技企业经营的项目（或产品）往往更新换代速度很快，一旦跟不上市场的变化，资产价值会大幅度贬值，从而σ2很大，而高科技企业的无形资产比重很大，即使有形资产，一旦过时，也仅具有很有限的价值，故α很大。另外高科技企业一般受到政府扶持，给予减免税收，使得有效所得税税率大幅下降，因此，高科技企业缺乏追求债务利息免税的动力，这几部分的共同作用决定了高科技企业的负债率很低（见表3.1或表3.2）。我们的模型能够从另一角度定量分析第三章最后给出的论点，即高科技企业债务融资的好处是很有限的，并且把经营风险、税率、破产成本等放在一个统一的框架内分析，从而更准确、更合理。

在永久性债务情形下，运用相机权益分析，我们可以得到债务估值公式，内生破产点，最优资本结构的解析表达式，在此基础进行的深入分析大多与我们在第一章所介绍的资本结构理论一致。特别地我们给出不同数据模拟的最优资本结构，可以看出，企业内部特征与外部特征不同，最优资本结构将有显著差异。一些企业最优负债比率高达90%以上，而另一些企业最优负债率则低于20%，因此笼统地把50%作为企业负债比率的标准显然是有问题的，我们能够解释如IBM等高科技公司低负债的原因。

然而，这一章给出的模型也有一些需继续完善的地方。首先，虽然永久性债务可作为长期债务的近似，但毕竟不等于长期债务，在实务中需通过数字仿真求解非永久性债务下企业的最优资本结构，这是一个艰巨的任务。其次，这里模型中实际假定有非常发达、完善的金融市场，现实中特别是中国目前还难以达到这个要求，如果没有完善的金融市场，就会有套利的机会，定价公式将难以发挥作用，相机权益定价技术将失去其理论基础。当然，只要有套利，就不可能均衡定价，因此，本书的模型也只能是现实中的一个近似。再次，资金短缺问题是发展中国家普遍面临的问题，而这里对此未作限制。现实中，可能有些企业无法股权融资，不可避免选择债务融资，或无法债务融资不可避免地选择股权融资，这些都会对资本结构产生影响，从而达不到或超过其最优资本结构，在股权资本或债务资本受到约束下的资本结构研究也有待以后进行。最后，滚动发行短期债务类似于长期债务，只要企业有偿债能力，资产增值有保障，短期债务是容易得到的。当然，短期负债过大可能直接使企业陷入财务危机中。我们将在下一章结合国有企业资本结构的研究进行一些阐述，以使我们的分析更具说服力。

3.4　本章小结

相机权益定价方法是金融工程中最重要的定价工具。企业债务是一种相机权益，从而可对企业债务运用相机权益分析技术，进而研究企业的最优资本结构。不同于传统的定性分析方法，我们建立的模型能够定量分析各因素对资本结构的影响，从而在一定程度上更具现实意义和可操作性。该模型的研究结果能够解释多数定性资本结构理论，并提供一些新的视野。具体来说，本章得到了如下几方面结果：

一、由于破产成本在资本结构研究领域的重要，我们考虑了破产成本对债务价值的影响，运用CCA方法得到一个包含破产成本的风险债务估值公式。该公式是Black ＆ Cox给出的公式的直接推广且更有意义。特别地，我们考虑了股利支付对风险债务的影响，从而能在资本结构研究中探讨股利政策对最优资本结构的作用，这在资本结构研究中尚不多见。

二、运用包含破产成本的风险债务估值公式，考察了纯混合兼并对企业债务价值的影响，从而能够分析混合兼并是否有助于缓和企业的债务压力，我们得出的结论是混合兼并不一定能改善企业的债务状况。

三、运用相机权益分析技术，结合资本结构的平衡理论或调整净现值法（APV），得到企业总价值及股权价值的表达式。再由股权价值最大化决定出企业的内生破产点，从而得到企业总价值、债务价值及股权价值的又一数学表达式。

四、利用债务价值与股权价值的表达式，考虑了资本结构调整对债权人或债务人的影响。证明了如下结论：①如果没有额外补贴，股权持有者将不会赎回债务，相反地，增发债务回购股份将导致股权价值增加。②如果没有额外补贴，如果破产后剩余价值很小，且对破产点不敏感，则原债权人不会愿意企业发行新的具有同等优先受偿权的债务，该结论能够解释在债务合同出现的限制发新债的条款。

五、给出了企业最大债务融资能力的数学表达式，并得出投资政策（企业经营风险）、股利政策对最大债务融资能力的影响。

六、得到了最优资本结构所对应的利息及最优负债比率L*的表达式，企业资产价值只依赖于投资政策、股利政策、破产成本、所得税税率及无风险利率。通过数据模拟得到关于最优资本结构的各因素变动及各因素相互作用对资本结构的影响。特别地，我们区分了企业内部特征（σ2，d，α）及企业外部特征（τ，r）对最优资本结构的影响，这种量化分析使资本结构理论研究更具现实意义。

【注释】

[1]迈尔斯在1984年发表了著名文章《资本结构之谜》（Myers，1984）之后，1993年又发表了继续寻求最优资本结构的文章（Myers，1993），说明金融经济学家们仍继续致力于此研究。

[2]卢卡斯（Lucas，1972）在穆斯（Muth，1961）工作的基础上发展了理性预期学派的思想，成为理性预期学派的领头人物，实际上卢卡斯早期的工作主要集中在投资理论，正因为投资者有理性预期，才能通过研究“均衡”对证券估价。当然“理性预期”是一个很强的假定，由于西蒙的“有限理性”，实际上理性预期也许只能被看做是一种近似或一种极限，这种近似或极限（也许是不断贝叶斯修正的结果）可以大大简化我们分析的实际问题，从而得出有意义的启示。

[3]这里企业的资产价值不同于企业价值，正如本书1.3.1中（1.1）式所指出企业的资产价值可看做VU，而企业价值可看做VL或本书1.3.2中式（1.2）中的VU与VL。企业的资产价值V实际上是企业资产现在与未来产生现金流的贴现和现值，其一般并不等于重置成本。

[4]利率r不仅可以是随机的，即是一随机过程，本身有自己的运动规律，而且即使不是随机的，其也可能随着时间而变化，即是时间的函数rt，这两种情况虽然更具现实性，但都较为复杂，因此在本书中，我们大多假定r为常数，即rt= r。

[5]我们综合了Merton（1974）的假定A.1、A.2、A.3、A.4、A.5或Merton（1977）的假定A.1以及Black ＆ Cox（1976）的假定a1、a3、a4、a5。我们把它们统称为关于金融市场的假定。

[6]Merton（1974）的假定A.7，Merton（1977）的假定A.2，Black ＆ Cox（1976）的假定a2均作出这样的假定。

[7]该假定或类似的企业资产价值过程的假定被认为是最关键的，Merton（1974）认为关于金融市场的假定实际上可以放宽，而连续性交易与企业资产价值的动态性正如在导出期权定价公式中关于股票价格的动态性一样是至关重要的。Black ＆ Cox（1976）曾讨论该方程的合理性，认为或许描述为一个不连续的跳跃过程也可能是重要的，但他们并未进行这方面的处理。关于其他的表示模型可参见Cox ＆ Ross（1976）。Fischer，Heinkel and Zechner（1989）也在此模型基础上讨论动态资本结构，Adersen ＆ Sundaresan（1996）运用资产价值的二叉树模型（其极限形式也为类似扩散过程）讨论了债务定价。

[8]关于Ito引理的导出及随机微分方程解的存在惟一性讨论可参见Oksendal（1985）或Mckean(1969)，其在证券市场的运用可参见Duffie（1996）。

[9]企业进行的支付一般是离散的，把这些支付看做是一种连续流动只是更方便。正如Black ＆ Cox（1976）指出，这种处理也是可以接受的，他们讨论了离散支付与最优停时问题（Optimal Stopping Problems）。当考虑息票债务时，息票一般是每半年或一年支付一次，Merton （1974）首先指出可以在式（3.7）把Cy用“Σi Cyiδ（τ-τi）”代替，其中δ（·）为dirac δ函数，Cyi为第i次的支付，τi表示到期的时间长度。

[10]Warner（1977）首先对破产成本进行了一些实证分析，发现破产直接成本大约为企业资产价值的5%，White（1983）、Altman（1984）、Weiss（1990）是用新的样本数据进行的统计计算，如Weiss (1990)是用1980年到1986年间31家破产企业的数据计算的。

[11]当然，国外与国内情况往往不具有可比性，国内企业破产中，政府干预、破产法规不健全等因素大大放大了破产成本，使得债权人的利益受到严重侵犯。参见：中国工商银行企业破产问题调查组，经济研究，1997（4）。

[12]这里给出的是比较静态（Comparative Statics）分析，比较静态分析是指固定其他变量，改变某个自变量对因变量的影响，Merton（1974）、Black ＆ Cox（1976）都作过比较静态分析。

[13]Cox ＆ Rubinstein（1979）使用了马尔科夫链方法。而Brennan ＆ Schwartz（1977）运用了有限差分方法求解类似的偏微分方程，而正如Brennan ＆ Schwartz（1978）证明的，这两种方法是很类似的，某些情况下是等价的。

[14]之所以在此导出F（V，t）关于V，t的表达式，是因为我们给出的企业资产价值方程（3.24）不同于默顿给出的方程（3.1）。在方程（3.1）中企业资产的预期增长率α是常数，而这里V是t与的函数，因为方程（3.24）的含义比方程（3.1）更广，但导出的方程（3.32）与方程（3.7）一致。

[15]为简单起见，我们这里未考虑股利支付，因此d = 0，把d = 0代入（3.16）中X的表达式可发现。而在边界条件，我们简化了破产成本假设，这里实际上g（VB）=（1 -β）VB，PB仍取相同符号，虽然其与式（3.18）中的PB并不一样。

[16]式（3.37）与（3.38）中的Wt可以不一样，但就得不到（3.42）式中的扩散过程，因而我们取为一样。另外，正如在股票指数期权定价时通常假设加权平均指数服从几何布朗运动与单个股票服从几何布朗运动是不一致的一样，式（3.42）中σ一般不为常数，但为方便起见，近似这样处理，这种处理就如同我们同时假设单个股票与股票指数均服从几何布朗运动一样，参见（Hull，1977）第十一章注释1。实际上，由于式（3.43）必然成立，这种近似处理不影响我们结果的讨论。

[17]这两种不确定性之间或许是等价的。事实上，当我们把企业资产价值V看做是企业产品价格P的函数时，同样可通过P的讨论来探讨V，但那样相对较为复杂，为更明确地看出V的轨迹对资本结构的影响我们分开来探讨，关于P的动态性对资本结构的影响，最近几年有大量文献，如Mello ＆ Parsons（1992），Mauer ＆ Triantis（1994）等。

[18]Dixit（1992），Dumas（1992）也从最优停时角度证明了类似的Smooth-pasting条件。

[19]Black ＆ Cox（1976）讨论了次级债务的定价问题。注意到我们未讨论其他更为复杂的债务，如可转换债务等的定价可在文献Brennan ＆ Schwartz（1980）中找到。

[20]这里给出的符号

[21]X=7对应的是低风险，低股利的企业，X=1对应的是低风险、高股利或高风险、低股利的企业，而对于高风险、高股利的企业如X＜ 0.05，由于实际上也难以债务融资，故我们未考虑。破产成本系数α= 0.7对应的是高破产成本型企业，α= 0.3对应的是平均破产成本型企业，公司所得税税率取τ=0.33及τ= 0.15是目前国内大多数企业的所得税税率，r取三个值，r =10%表明经济处于高速增长期，r =5%表明经济处于快速增长期，r = 1%表明经济缓慢增长。注意到r的取值会改变X的值（固定σ，d），但正如前面分析的，X随r的增加而增加，因此当r = 10%，而X =7时，σ与d必须取比表3.1中更小的值，即更安全的企业。