不确定环境下的资本成本与投资决策研究

第二章　引入风险后的资本成本与投资决策研究

金融理论对风险的处理已渐趋成熟，然而在莫迪利亚尼与米勒发表他们的著名文章之前，金融理论对风险的差异还难以处理，所以在MM定理的假设中，风险被假定是一样的。正如我们所指出的，不同企业、不同项目由于其资产的特征不一样，其产品与市场的依赖程度不同，应该说具有不同的风险，因此，对于引入风险后资本结构对资本成本的影响是值得探讨的，这无论是在发达的市场经济还是在转轨经济中都有重要实际意义。这一章我们在不考虑各利益主体的冲突下，单纯考虑资本结构与资本成本的关系，并对传统的投资决策方法即净现值方法给予了改进。

2.1　投资决策与资本成本

一般在资产负债表的左边是企业的资金使用，即企业把资金投向哪些资产、哪些项目，其右边是资金的来源即融资的方式，是股权融资还是债务融资。^[1]正如MM定理指出，在MM定理假设成立的条件下，左边的决策即投资决策与右边的决策即融资决策独立，更确切地说企业价值与资本结构无关。然而MM定理中未考虑风险，特别是未考虑资本结构对股权和债务风险的影响，在引入风险后的讨论我们放在后面，这里我们暂不计入风险，只给出投资决策的标准及资本成本的定义，为后面的分析做准备。

2.1.1　投资决策的标准

企业可以在各类资产中进行投资。这些资产既包括有形资产如机器设备、厂房、土地等，也包括无形资产，如专利、技术等。投资目标或资本预算决策（Capital Budgeting Decision）是为了发现哪些资产有价值（即收益超过成本），而资产的价值正如我们所了解的可以用净现值（即NPV法）来计算，因此，投资决策的标准是如下两个等价的法则：^[2]

①净现值法则，即接受净现值大于0的投资项目。

②回报率法则，即接受投资回报率超过其资本成本的项目。

因此，除非特殊说明，我们只需考虑净现值法则即可。我们的经济学直觉告诉我们：在一个接近完全竞争的行业内很难发现有净现值为正的项目，当一个行业进入长期竞争均衡时，该行业的所有资产预期收益一定等于资本的机会成本，不多也不少。然而在一些非竞争性行业仍有大量净现值为正的项目等待投资。一般来说，以下几种情形均可能产生正的净现值，比如，首先引入新产品、发现核心技术、有进入壁垒、产品间差异、组织创新等，这些都能产生所谓的经济租（Economic Rents）即收益超过其机会成本。

那么企业在进行投资决策时是否需要考虑股东的偏好呢？由于我们这里未考虑利益冲突，管理者将以股东财富最大化作为决策标准。一个企业的股东可能有成千上万，甚至几十万，这些股东关于未来消费的偏好显然不可能完全一致，在这种情形下，管理者不可能根据某些股东的意愿行事。美国著名经济学家费舍（Fisher，1930）提出了费舍可分性原理，解决了在确定性情形下的这个问题，即在完美（Perfect）与完备（Complete）资本市场，企业最优投资决策与股东的个人偏好无关。而企业最优决策目标就是最大化股东财富的目标，这个目标就是最大化企业的净现值（NPV）。因此，正净现值项目必然增加股东的财富。特别地，当一家企业宣布对一个好的项目进行投资时，大多能导致其股票价格的上涨。^[3]实际上，即使在不确定的世界里，可分性原理在一定条件下仍能成立，只是企业只须最大化其股票价格就可最大化现有股东的预期效用，这与企业投资于净现值为正的项目的决策是一致的。^[4]

净现值的计算主要依赖于两个要素，一个是项目寿命期内的净现金流量NCF，另一个是贴现率。一般来说，一个企业的净现金流量依赖于其资产收益，而贴现率依赖于资金的成本或资金的来源。我们把净现值公式写成如下形式：

这里贴现率r表示资金的成本，为第t年的折现系数，I0为期初投入。目前，在投资项目评估中，国内常见的做法是用行业基准利率来折现。

然而，传统的净现值法计算净现值从而判断项目是否可行会面临许多难题，对于风险的现金流量我们可以利用无风险利率贴现来准确定价，但当现金流量有风险时，如何计算其净现值就会产生问题，比如，对于风险资本项目，往往是高风险项目，项目各年的净现金流量不确定，可能发生很大波动，在全部股权融资时，如何计算项目净现值。另外，当项目不仅有股权融资，而且还用债务融资，又如何计算净现值，这些都是本章要解决的问题。因此，当引入风险与债务后，NPV法的计算相对更为复杂。

2.1.2　资本成本的定义

在进行投资决策之前，必须先对资本成本有所了解和估算，这样才能决定是否进行项目投资。不同的资金来源往往成本不同，而融资成本又依赖于不同资本所面临的风险。由于股东往往能决定是否对某项目投资，因而他们只会接受使得他们财富增加的项目，这样，项目必须能够产生足够多的净现金流满足不同投资者（债权人与股东）的风险调整的回报率，即除了能支付他们原先提供的资金本金外，还能有一定的剩余增加股东的财富。从这个意义上说，资本成本定义为能被股东接受的项目所能产生的最小风险调整回报率（Minimun Risk-adjusted Rate of Return）。

这里我们来考察一种简单情形，即假定所有项目具有相同的风险，而且不同资金来源有相同的风险，也即股权与债务融资是无差异的，此时投资金额将由资金的供求决定，而且资本的供给即资本的边际成本为常数，资本的需求由投资的边际效率决定。见图2.1。

图2.1　等风险项目的资本供给与需求

在项目能产生E（Rj）收益率情况下，资本的供给是无穷大，即供给曲线为资本的边际成本线，因而有无穷弹性。E（Rj）收益率也可看成资本供给的机会成本，而投资的边际效率是随投资量增加而下降的，即边际收益递减，从而决定最优均衡投资量，这个图虽然过分简化了资本成本与投资量的关系，但它显示了这样一个道理，即资本的边际成本越高（外部的获利能力越大），最优投资数量越低。

莫迪利亚尼与米勒（Modigliani and Miller，1958，1963）在他们著名的著作中给出了资本成本的数学表达式，在给出表达式之前，他们同样做出了严格的假定（见1.3.1给出的MM定理的假设条件）。

在引入公司税后，首先考虑一个不负债企业（Unlevered Firm）（即所有资本来源于股权融资）的价值：

这里FCF =（Re v - VC - FCC - dep）（1 -τc）= NOI（1 -τc），为每年的税后净现金流量（假定不变）。

其中：Re v为销售收入，VC为经营可变成本，FCC为固定成本，dep为折旧，NOI为税前净收入，τc为公司所得税税率，ρ为全部股权融资企业的贴现率（ρ也可看做是企业资产的回报率）。类似于不负债的企业价值，可得出负债企业（Levered Firm）的价值表达式（这里资本成本概念未考虑现金流的波动，也未考虑破产成本、风险等）：

其中Kd为债务面值D的利息，Kb为无风险债务的贴现率，从式（2.3）可看出，企业价值由两部分现金流贴现求和所得，一部分是股权价值，一部分为债务价值，记为：

结合式（2.2）与式（2.3）得：

特别地，如τc= 0即无公司所得税，则：

式（2.5）即MM定理，即不考虑公司所得税，在前面的假设下，企业价值与融资结构无关，此即MM无关论。这个定理本身说明了一个重要的结论，也是本书重点探讨的问题，其副产品是关于资本成本的表达式。

特别地，如每年净现金流固定增长，即资产本身增值（未考虑投资），如ENOIt= E（NOIt-1）（1 + g），g ＞ 0，则其类似于Goldon的股利增长模型

相当于只改变股权资本的成本，不改变MM得出的结论，但如更为复杂的情形，特别是资产值本身会波动的情形，我们将在后面讨论。

回顾前面对资本成本的定义，要使得原有股东财富增加，对新项目投资所产生的回报，必须超过股东与债权人提供资金的机会成本。因此，可以考虑新项目投资ΔI产生的回报ΔVL，则由式（2.4）得回报率为：

把ΔVL分解为四部分，即

其中上标0表示原来的股东或债权人，而n表示新股东或债权人，由于假定无论是新债务还是旧债务均无风险，故ΔB0= 0。

而ΔI要么由ΔSn产生，要么由ΔBn产生，故：

因此

故要使原股东满意，必须

把式（2.7）代入可知

因此

式（2.11）左边表示单位新投资带来的税后净现金流，右边是资本的机会成本，即资本加权成本，从而资本加权平均成本为：

式（2.12）即为MM关于资本成本的定义。首先注意到MM并未考虑风险调整回报率，其次注意到如τc= 0，则WACC =ρ，与资本结构无关。可以看出，在考虑公司税后，在混合融资（即债务与股权）下，企业的资本成本有所下降，从而这可以看做是债务融资的收益，然而经常引起争议的是关于ΔB/ΔI的准确描述，因此，莫迪利亚尼与米勒（Modigliani and Miller，1963）专门就此解释为：“如果把B*/V*作为企业长期‘目标’资产负债率……则企业可以假定，至少是一种近似，对于任何投资dB/d I = B*/V*”，这样边际负债与平均负债相等。

当V*= B*+ S*时，则重新表述为：

从该式可看出，当B /（B + S）→1时，WACC达到最小，即当所有资本均来自债务资本时，企业的资本成本达到最小，然而由于破产成本的存在，实际上我们很难看到完全用负债来经营的企业。类似地，MM给出了负债企业股权的成本与非负债企业股权成本的关系式：

令即维持目标资本结构，则上式改写为：

此即MM定理的命题2，只要ρ＞ Kb，上升时，KS也上升，即MM指出，虽然债务资本的成本相对较低，但随着债务资本的增加，股权资本的成本上升，特别地，如果τc= 0，则债务资本的低成本正好被股权资本增加的成本所抵消，而使得加权平均成本不变，即WACC =ρ。

另一方面，我们会发现，当企业既用股权又用债务进行融资时，如果企业对债务支付回报率为Kb（Kb为融资承诺利率），对股权资本支付回报率Ks，由式（2.14）可看出，只要企业资产回报率超过债务成本，即ρ＞ Kb，则对负债企业的股权资本回报率会高于无负债企业时的ρ，因此，企业乐于债务融资。另外还可以用股权资本与债务资本所形成的资产比率，来决定企业资本的平均成本，即资本的加权平均成本WACC表示为：

式（2.15）是根据相应对资产的回报要求给出的资本成本，也是不依赖于MM定义的资本成本公式。可以证明，在MM的假设下，式（2.13）与式（2.15）是等价的，因此，传统的资本成本定义（2.15）与MM定义是一致的，图2.2给出在有公司税与无公司税时资本成本作为资本结构的函数关系。

图2.2　资本成本与资本结构的关系

2.2　引入风险后的资本成本

一般来说，风险可划分为系统性风险与非系统性风险，非系统性风险可以通过证券组合、分散投资而得到有效控制，而系统性风险是与市场共存的风险，难以通过分散投资转移，因此，我们这里仅讨论系统性风险。正如一般证券一样，在我们研究企业的资本结构中，股权资本与债务资本均具有一定的风险。在均衡定价的框架下，均可以借助CAPM来表达其风险，同时，期权定价模型也可以被用于对股权资本与债务资本的风险刻画。

2.2.1　系统性风险与资本成本：CAPM的处理

资本资产定价模型在20世纪60年代提出之后，人们不仅可以用它解决证券市场中证券的定价问题，特别重要的是，它提供了对风险的估价，从而能够考虑任何有风险的情形，对经济学是一个巨大的贡献，诺贝尔经济学奖授予其发现者是合情合理的。在考虑MM所提供的资本结构理论时，同样可以把风险引入，特别地，它比MM关于资本成本的考虑更具有实际意义。

CAPM可以描述为如下均衡定价方程：

其中，E（Rj）为资产或证券j的预期应得收益率，Rf为无风险利率（在静态模型保持为常数，在动态模型中可以变化），E（Rm）为市场证券组合的预期收益率。表示两变量Rj、Rm的协方差，VAR（Rm）表示Rm的方差。CAPM说明项目资产j因为有风险，从而不仅要获取无风险收益率，还要额外获取一风险费，即［E（Rm）- Rf］βj依赖于其β值。

根据CAPM，βj反映了项目的系统性风险，任何一种证券或项目资产，无论其风险（用β值反映）如何不同，所有证券都会准确地落在证券市场线（Secutity Market Line即SML）上。这样，实际上提供了一种刻画不同风险的方法，我们可以回忆一下，在MM定理假设中，所有项目风险是同一类的，即有同样的商业风险或经营风险，按照数学语言，这实际上假定项目i的现金流量CFi是任一项目j的现金流量CFj的常数倍，即CFi=λCFj，λ为常数。引入风险后，这一假设可以放松，我们来比较一下MM关于资本成本的定义与CAPM关于资本成本定义的差异。

首先，在MM定义中，债务是无风险的，因此，债务的收益率（债务成本）Kb= Rf，其风险系数βb= 0，而在CAPM的定义中，债务作为一种证券或资产，可对其风险定价，可得到其CAPM方程：^[5]

βb可以不为0。

其次，在MM定义中，无负债企业的股权回报率ρ是不考虑风险的（因为所有项目风险一样），而在CAPM的定义中，无负债企业的股权回报率ρ同样可在CAPM框架中得到定价，即：

βU为企业资产的风险大小。

再次，根据MM定义，负债企业的股权资本的收益率（是股权资金成本）Ks=ρ+（ρ- Kb）（1 -τc）B/S，可看做是资本结构、无负债企业股权资金成本、债务成本的函数，显然在这种情形下，只要ρ＞ Kb，即资产回报率超过债务承诺，则Ks＞ρ，但根据CAPM定义，由于风险不同，从而有负债企业的股权资本的收益率（或成本）仅用其风险系数βL表示，即：

MM假定债务是无风险的，即βb= 0，即是说债券价格对于利率不敏感，而且要么无企业违约风险，要么是能够把违约风险完全分散化（即系统性风险为0），如果我们保持MM的这个假定成立，则我们运用MM关于负债企业股权资金成本的定义，可以导出βU与βL的关系，即无负债企业的股权资本系统性风险与同样资产的负债企业的股权资本的系统性风险的关系。

实际上，由Ks=ρ+（ρ- Kb）（1 -τc）B/S，把式（2.18）与式（2.19）代入方程左右两边，注意到假定βb= 0，从而Kb= Rf，则经过简单化可得如下关系式：^[6]

由于1 -τc＞ 0，B/S ＞ 0，则βL＞βU，这说明，随着负债的增加，负债企业股权资本的风险βL越来越大，其最小值为βU。一般来说，βU是难以实证观测的，而βL则可通过股票市场证券交易的数据计算得到，由于βU实际上代表着企业资产经营的系统性风险，因而我们可以利用βL的数据来估计βU的值，从而说明企业经营风险。

当MM给出资本平均成本时，一般资本成本的定义为：

这里Kb与Ks分别由式（2.17）与式（2.19）决定，这也就是CAPM所给出的资本成本的定义。一般来说，ρ是难以直接观测的，因而MM关于资本成本的定义，实际很难运用，然而把它与CAPM的资本成本定义结合起来，会发现能够间接计算出ρ，从而当资本结构调整时，可以用MM定义计算出调整后的资本成本。实际上，由证券市场的数据可以计算出式（2.19）中的βL，从而立即可得到Ks，在假定债务风险系数βb= 0时，可利用式（2.21）求出WACC，而又由两种资本成本定义等价（βb= 0时），则由求出ρ，再用新的代入求出新的资本成本。当然这只能是一种近似计算，因为这里未考虑债务增加（调整资本结构）对股权资本风险的影响，当我们运用MM定义的Ks=ρ+（ρ- Kb）（1 -τc）B/S时，实际并不考虑风险，而根据CAPM，风险对Ks的影响很大。

2.2.2　风险债务下的资本成本：OPM的处理

在引入风险以后，我们可以用CAPM对不同风险进行估价，但CAPM只能是静态的结果，根据前一小节讨论的结果，CAPM的定义把资本成本（股权资本成本及债务资本成本）仅归结为其风险系数，其虽然能够处理有风险的情形，但却未得到类似于MM定理命题2即式（2.14）的结果，我们难以发现资本结构变化对股权资本成本与债务资本成本的影响。在这里，我们运用期权定价模型（即OPM），结合连续时间的CAPM探讨风险债务下的资本成本，并与MM进行比较。

期权定价模型（Option Pricing Model，即OPM）最早由布莱克与舒尔斯在1973年的文章《公司负债与期权定价》中提出（Black ＆ Scholes，1973），默顿（Merton，1973a）等人给予发展，并迅速在交易所得到广泛应用。1973年美国正式推出期权交易，从而使得期权定价模型不仅在实践中得到检验，而且也得到了理论界的承认，1997年诺贝尔经济学奖授予OPM的开创者默顿与舒尔斯就是一个例证。^[7]期权定价模型不仅在衍生证券定价中得到广泛的应用，而且也被广泛应用到公司财务等领域，它为许多研究领域提供了新的视野。

首先来说明债务、股权同期权的关系，布莱克与舒尔斯（Black ＆ Scholes，1973）第一个指出了有负债企业的股权实际上是关于企业价值的一个看涨期权（a Call Option）。假定企业只有两类资本来源：股权资本与风险债务资本，债务是零息票债券（即不付息，到期支付面值，因而发行价低于面值），有面值为D，到期期限为T（从现在算起），在到期之前，债权人不能强迫企业破产，企业也不被允许支付股利。实际上，债务相当于股东持有的一份看涨期权，因为在债券到期日，如果企业的价值V超过债券面值D，则股东支付债券面值，从而实现看涨期权（Exercise Call Option），得到剩余价值。如果V低于债券面值D，由于有限责任，股东放弃看涨期权，即对债权人违约，从而把企业价值全部交给债权人。因此，股东到期的财富S为：

同样，债权人持有的债券实际上可看做是一个无风险债券B减去一个欧氏看跌期权P（European Put Option）即B - P，看跌期权可理解股东有权力把企业出售给债权人以换取曾经承诺的支付，在到期日，债权人接受的财富为：

类似于默顿（Merton，1974）的假定，设企业价值V服从扩散型随机过程（a Diffusion-type Stochastic Process），满足随机微分方程（Stochastic Differential Equation）：

其中，α是企业资产单位时间的瞬时预期回报率（Instantaneous Expected Rate of Return），σ2是企业资产单位时间回报的瞬时方差，α，σ2均为常数。而dz为一标准高斯—维纳过程（Standard Gauss-Wiener Process）。^[8]

为了得到风险债务下的资本成本，我们还必须使用默顿（Merton，1973b）给出的CAPM的连续时间修正（Continuous- time Version），即：

其中E（ri）表示资产i的瞬时预期回报率（或收益率），βi为资产i的瞬时系统性风险，βi= COV（ri，rm）/ VAR（rm），E（rm）为市场证券组合的瞬时预期回报率，rf为无风险资产的瞬时非随机回报率。^[9]

我们假定，无交易成本，也不考虑税收，且对企业资产价值V服从的随机微分方程（即2.24）有一致预期（Homogeneous Expectations），由于企业价值由股权价值与债务价值组成，则V =（B - P）+ S，其中B - P为风险债务价值，为低风险的索取权，而S为股权价值，为高风险的索取权。当我们把股权价值S与债务价值B-P看做是基于企业价值V的期权时，运用期权定价理论已有的成果，立即可以得出如下暗示，股权价值S作为V的欧氏看涨期权，将随着V的增加而增加，随着企业价值V的波动增加（即σ2增加）而增加，也随着无风险利率rf的增加而增加。特别值得注意的是，并随着到期时间T的增加而增加。按照数学语言，欧式看涨期权S，可看做是标的资产V，实现价D，标的资产回报的瞬时波动方差σ2，到期日T，无风险利率rf的函数，记作：

则S关于各变量的偏导数的符号如下：

从这些暗示中，我们知道，正如詹森与麦克林（Jensen ＆ Meckling，1976）指出，由于股权的期权性质，股东会采取使企业资产波动更大的策略，即选择风险更大的项目，从而增加股权价值，即，从而产生资产替代效应。

现在，我们设定D，σ2，T，rf已知，仅把S看做是V与t的函数，即S = S（V，t），则由V服从随机微分方程式（2.24），运用Ito公式我们可以得到S关于V与t的微分方程：

这个方程说明了股权价值（或股票价格）变化是企业价值变化dV、企业价值回报的瞬时方差σ2等的函数，在方程两边除以S，并对dt趋于0取极限，则：

意识到是股权价值回报率rs，为企业资产回报率rv，则上式可写为：

把上述连续时间CAPM运用到股权的系统性风险βs，与企业资产价值的系统性风险βv，则：

由式（2.30）与式（2.31），立即有：

为得到的值，可以利用Black-Scholes的期权定价公式，即（B - S）公式，对看涨期权S用B - S公式，则：

其中S，V，D，rf，T如前定义，而N（·）表示正态分布函数。

由式（2.33）立即有：

把上式与式（2.33）代入式（2.32）可得：

这个方程反映了股权资本的系统性风险与企业资产（即无负债企业股权）的系统性风险的关系。^[10]由于，因此，可以得出βs≥βv＞ 0，这一结论说明负债企业股权的系统性风险大于未负债企业股权的系统性风险，这一结论与式（2.20）的结论一致。特别地，当我们假定βv的风险特征不随时间变化时，对式（2.35）求偏导，可得：

可以看出这些表达式与式（2.27）给出的结论是一致的，因为当股权价值S增加时，其系统性风险下降即更安全。

为了得到股权资本成本与资本结构的关系，还可以作如下推导，结合CAPM与（2.35）的第一个等式，则：

而又由CAPM，代入式（2.36），可得：

该式说明股权资本成本与资本结构的关系，即随着资产负债率的增加（从而增加），只要Erv＞ Rf，则股权资本回报率（从而资本成本）上升。这个结论与MM定义中，的含义是一致的。

同样，我们可以类似地考虑债务资本的系统性风险βb，在一个无税及无破产成本的世界里，债务资本价值可写为B = g（V，t），即依赖于企业价值V与t，同样可运用Ito公式，得到：

与式（2.29）类似，得到：

结合CAPM，可设：

借助于默顿（Merton，1974）给出的关于公司债的期权定价公式，我们可以得到：

再次借助连续时间的CAPM，结合式（2.40）、（2.41），类似于（2.37）的推导，我们有：

这是由OPM给出的债务资本成本与资本结构的关系，这个关系在MM定义与CAPM框架中均未得到讨论，可以看出风险债务的成本应等于无风险利率加上风险费，即，随着资产负债率的增加，将增加（这可以通过代入不同的资本结构实证算出），从而风险债务的要求回报率即成本将增加。(www.xing528.com)

结合式（2.37）与（2.42），通过OPM与CAPM的连续形式，可以得出这样的结论：随着资本结构负债的增加，股权资本与风险债务资本的风险费均增加，从而各自的要求回报率即资本成本均增加。但是加权平均资本成本均不变，Hsia（1981）给出了简单证明。实际上由WACC的定义，把式（2.37）和（2.42）代入，并利用N（-d1）= 1 - N（d1），则：

因此，风险债务的引入不改变加权平均成本，MM定理仍然成立，但在OPM与连续形成CAPM下，我们得到了一个不同于MM定义的资本成本、股权资本成本与债务资本成本，下面给出其图示，见图2.3。特别地，这里给出的结果也比式（2.17）与式（2.19）更具体，其明确指出βb =即资本结构对βb，βs的影响。

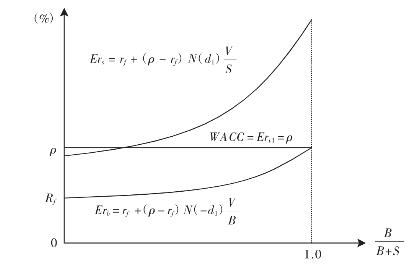
图2.3　无公司税情况下风险债务与资本成本

2.3　风险项目的净现值法研究

现代金融理论已经能很好地处理风险与预期回报之间的关系了，CAPM是最重要的工具之一。然而即使在CAPM出现之前，一个企业的财务主管也会意识到项目的风险与收益之间的关系。他们直观地认为，在其他情形一致时，一个安全的项目比一个风险的项目更好，即使其收益可能更低一点，因而为了回避风险项目投资，他们往往对风险项目的现金流量作出更保守的估计，或者他们会使用更高的贴现率。这种直觉往往是正确的，正如CAPM指出，当一个人承担风险更大的投资时，其往往要求有更高的回报率以补偿其承担的更高的风险。然而CAPM是一期静态模型，并不能直接用于净现值的计算，我们这里首先给出了风险资本（Venture Capital）项目中如何引入确定性等价收入来计算净现值，^[11]然后用这种方法考察了一个负债项目的净现值的计算，并与其他已有结果进行了比较。

2.3.1　风险资本项目的净现值法研究^[12]

净现值法（即NPV法）是投资项目评估的主要方法。所谓净现值是将项目整个寿命期内发生的年度现金流入量和现金流出量的差额，逐年按固定利率分别折现而得到的值。因此，净现值公式为

这里NCFt为项目在t = 0，1，…，n年每年的净现金流量，r为折现率，为第t年的折现系数。折现率r应等于资本市场中长期贷款的实际利率，目前，常见的做法是用行业基准利率来作折现率。

然而，对于风险投资项目，运用公式（2.43）来计算项目的净现值从而判断项目是否可行会面临许多难题。首先，风险投资项目往往是高风险项目，这里的高风险指的是项目各年的净现金流量往往不能准确预计，而且可能发生很大波动。因此，每年净现金流量在不同情况下会出现不同的值，这在公式（2.43）中未考虑。其次，由于风险投资项目净现金流量的不确定，投资者承担了更高的风险，投资者必须获得相应更高的回报。折现率必须能反映风险的大小才符合投资者的效用最大化。由此可见，对于通常的净现值公式（2.43），很难运用于风险投资项目，运用公式（2.43）计算得到的净现值为正的项目未必是好项目。因此，有必要对公式（2.43）进行改进。下面，我们考虑用资本资产定价模型（即CAPM）来修正净现值公式，得到一个能反映项目风险的净现值公式，并给出了一个实例分析。

夏普等人在20世纪60年代得到资本资产定价模型（CAPM）。从此，人们可以对风险资产进行定价，通过求出该风险资产的β值，我们有：

这里βj为风险项目或资产j的系统性风险，其中Rj为风险项目j的投资回报率，Rm为市场证券组合M的投资回报率，Rf为无风险利率，E为期望算子，COV（Rj，Rm）为协方差，VAR（Rm）为方差。

CAPM说明，风险项目j的应得回报率E（Rj）等于无风险利率Rf加上风险费（Risk Premium）即［E（Rm）- Rf］βj。

式（2.44）还可改写为：

其中，当把协方差COV（Rj，Rm）看做风险度量时，则λ即为风险的估价，即单位风险的价格。

我们把1 + E（Rj）= 1 + Rf+λCOV（Rj，Rm）称为风险调整回报率，即因为增加了风险，从而必须得到比无风险收益更高的回报。因此，对于风险投资项目，折现率不应是1 + Rf，而必须是风险调整回报率1 + E（Rj）。然而，直接运用1 + E（Rj）去代替1 + Rf仍会出现问题，因为每年的风险不等，要计算每年的1 + E（Rj），必须要计算COV（Rj，Rm）。而项目投资往往是期初投入，寿命期内收回，难以计算各年的Rj，另外Bogue ＆ Roll（1974）指出，对于多期风险项目，用单期风险调整回报率来贴现各年的现金流量往往是不正确的。因此，我们必须把Rj转化为各年的净现金流量NCF。

下面，我们首先来看一期情形，假定项目j期初投入为P0，期末得到不确定回报P1，由回报率定义：

从而 ，而由CAPM，E（R）j= Rf+λCOV（Rj，Rm），立即有E（P1）= P0［1 + Rf+λCOV（Rj，Rm）］，写成贴现形式，则把代入分母，可得：

这里E（P1）-λCOV（P1，Rm）称为P1的确定性等价收入。可看出，对于风险项目，一方面可以用更高的折现率来折现，另一方面，也可以用风险收入减去一项，产生确定性等价收入，再用无风险的折现率来折现，得到现值。

然而公式（2.46）只是一期的情形，对于多期，把P1换成每年的净现金流量NCFt，我们尝试用逆向递推法来推导其折现公式。首先，对于第t年的净现金流量NCFt，t = 1，2，…，n，运用公式（2.46）可先将其折算到第t - 1年

其中Rmt为第t年的市场证券组合的回报率，为第t年的风险价格，Rft为第t年的无风险利率，t = 1，2，…，n。

其次，把Pt-1与第t - 1年的净现金流量NCFt-1折算到第t-2年，可得：

依此类推，逆向推算至第0年，我们有：

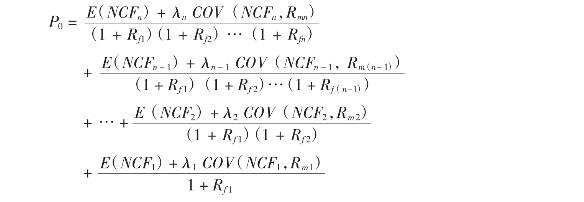
注意，我们这里把每年的净现金流量变成确定性等价收入之后，就不再考虑其以前各年的风险，即假定t年之前的风险因素，并不影响t年的净现金流量，因此，对以前各年的折算就简单地用各年的无风险利率来折算。

在公式（2.47）的基础上，再考虑期初投入I0就可得到运用CAPM消除风险后的净现值公式：

其中，NCFt为第t年的净现金流量，Rmt，Rft分别为第t年的市场证券组合的回报率及无风险利率，λt为第t年的风险价格，

比较公式（2.43）与公式（2.48）可看出，由于λt≥0，而COV（NCFt，Rmt）也往往大于0（也有少数例外情况），因此确定性等价收入E（NCFt）-λt COV（NCFt，Rmt）小于E（NCFt），故一般用公式（2.48）计算得到的净现值更小，因此风险投资者投资的项目必须有更高的预期净现金流量。风险投资公司会对大量的申请项目进行选择，最终确定的投资项目将是申报项目的1‰左右。

我们考虑两个风险投资项目，期初均投入I0= 500万元，为便于比较，项目寿命期均为3年。在每一年里均有三种可能状态，给定其每一种状态的主观概率P，相应的市场证券组合回报率Rm，无风险利率Rf，以及各种状态下的净现金流量NCF的估计值，数据如表2.1。由于两项目的净现金流量不同，故风险不同，我们试运用改进后的净现值公式（2.48）进行项目评价。

计算两项目净现值步骤如下：

步骤1：计算寿命期内每年市场证券组合的平均回报率E（Rm）

表2.1　两风险投资项目在寿命期内的各项数据（I0= 500万元）

以及各年的λ值，

则可计算E（Rm1）= 1/3×0.16 + 1/3×0.10 + 1/3×0.13 = 0.13

类似地，E（Rm2）= 0.12，E（Rm3）= 0.11

类似地，λ2= 55.556，λ3= 36.364

步骤2：计算两项目在寿命期内的平均净现金流量E（NCFt）及协方差

COV（NCFt，Rmt）= E［NCFt- E（NCFt）］［Rmt- E（Rmt）］

对于第1个项目E（NCF1）=1/3×300 + 1/3×100 + 1/3×200 = 200

类似地，E（NCF2）= 340，E（NCF3）= 290

类似地，COV（NCF2，Rm2）= 3.6，COV（NCF3，Rm3）= 3.1

对于第2个项目，E（NCF1）= 1/3×200 + 1/3×100 + 1/3×300 = 200

类似地，E（NCF2）= 340，E（NCF3）= 290

COV（NCF1，Rm1）= 1，COV（NCF2，Rm2）= 0，COV（NCF3，Rm3）= 0.1

步骤3：运用公式（2.48）分别计算两项目的净现值。

对于第一个项目，把其相应数值代入公式（2.48），则：

类似地，把第2个项目数据代入公式（2.48）可得：

从上述计算结果可看出，虽然两项目各年的平均净现金流量相等，但考虑到风险后，第1个项目的净现值为负，第2个项目的净现值为正，可排除第1个项目。而如果仅把平均净现金流量用公式（2.43）计算净现值，则两项目净现值相等，且均为209.04。可见，修正后的净现值公式对于风险投资项目更有效。

2.3.2　引入债务资本的风险项目净现值法研究

前面，我们已经指出，在一个理想的MM世界里，所有融资决策是无关的，企业可以假定自己是完全股权融资而考虑投资。然而，由于现实世界与MM的框架有所差异，因而往往融资决策对投资决策是有影响的，特别地，由于债务的税赋效应以及项目本身的风险，我们必须对前面的净现值方法再作调整，使之能用于资本结构下风险项目的投资决策。前面我们给出风险资本（完全的股权资本）项目，用确定性等价收入给出的净现值计算方法，而CAPM对资本成本的定义我们也在2.3.1中给出，这里我们给出在有公司税及项目风险下的净现值计算公式。

一般来说，我们可以有两种方法考虑资本结构对投资决策（NPV）的影响，一种方法称为调整现值（Adjusted NPV，简记为APV）法，它是先假定项目完全股权融资，计算出其净现值，再加上资本结构对NPV的影响现值，如税盾（Tax Shield）、发行成本等，这里税盾的多少往往依赖于融资法则，即采取固定债务量融资，还是固定债务比例融资。在固定债务量融资中，税盾值相当容易计算（即每年大约多少利息免税），而在固定债务比例融资时，由于项目未来的市值是不确定的，依赖于项目的风险，因而难以确定。另一种方法称为调整贴现率方法，这种调整往往是向下调整，让贴现率更小，因为债务有税收优惠，因此，常用的贴现率称之为税后加权平均成本。实际上，由于债务融资除了有税盾效应外，还有诸多优点与缺点，如减少了股权代理成本，增加了发行成本（也包含债务代理成本），改善了信息不对称，等等，这些都可以在调整贴现率中考虑，只是由于许多因素难以量化，所以，大多数学者仅考虑了税赋效应。

正如在2.3.1中指出，MM（Modigliani ＆ Miller，1963）在永久性现金流量与永久性债务水平的假定下，给出了调整的资本加权平均成本。

其中r表示资本的平均成本，其依赖于企业经营风险，实际上也是企业无负债时的股权资本成本ρ。由于有公司税，故r*＜ r。Miles ＆ Ezzell（1980）给出新项目融资在债务比率为常数下的调整的加权平均成本公式：^[13]

其中rb为借款的利率，L为项目的永久性负债比率（从而企业必须始终调整其负债使负债比例为常数），r的含义同MM的公式。用这两个加权平均成本贴现现金流就可得到MM及Miles-Ezzell的净现值公式。

不同于上面所给出调整的加权平均成本公式及相应净现值公式，我们将在CAPM框架内及2.3.1给出的结果基础上，给出资本结构下风险项目的净现值计算公式。首先根据CAPM的定义，，则式（2.21）改写为：

其中Kb、Ks分别由式（2.17）、（2.19）决定，即：

βb、βs分别为债务资本与股权资本应得回报率的风险系数，由下面两式决定：

则：

实际上r*已经是税后调整的资本加权平均成本，如果能准确预测项目寿命期内各年的现金流量，根据该项目的所得税税率τc、资本结构L、资本市场的相应数据E（Rm），βs，βb（βs与βb可由与该项目内容及资本结构类似的企业的股票市场与债券市场的数据计算得出），就可计算出r*，把r*代入式（2.43）即可得项目净现值。然而正如我们在2.3.1所讨论的，当项目的现金流量具有不确定性时，上述计算（用平均NCF计算）将导致投资决策失误，因此，我们仍可用确定性等价收入来处理项目的风险。

由式（2.55），利用β系数的定义及协方差性质。^[14]

同样，我们先来看一期情形，由则而由式（2.56），则：

则化简可得：

其中称它为单位风险的价格，EP1-λCOV（P1，Rm）称为P1的确定性等价收入。

2.4　负税盾效应与股权稀释权衡下的企业融资行为分析

MM理论认为：在无公司所得税的情况下，企业的资本结构不影响企业的价值和资金成本；在有公司所得税的情况下，企业的价值随着负债比例的增加而增加，当负债达到100%时，企业价值最大。利息的抵税作用，对投资者来说意味着可获得更多的可分配经营收入。似乎也意味着在尚无或不考虑负债的负面影响（如破产成本，代理成本）时，企业会倾向于负债融资。并且在其他条件相同的情况下，企业的边际所得税越高，负债融资的可能性越大。实际上，利息的抵税作用对于企业（原有）股东而言不但没有好处，反而减少其对息税前利润的分割，即负债融资对股东有负税盾效应。在公司以当前股东利益最大化为决策目标的合理假设下，企业的融资决策是负债融资对股东的负税盾效应与股票增发的股权稀释作用的权衡结果。并且证明公司所得税税率的高低并不影响企业的融资决策。

基本假设：①企业没有破产成本、负债代理成本；②企业的经营收入不因负债的变化而变化；③公司决策以当前股东利益最大化或企业股票价值最大化为目标；④企业只有负债、普通股、内部融资三种融资方式。

相关变量：企业当前价值为V = S + B，其中S为企业普通股市价，B为负债的市价，对应的平均利率为r0。企业原有项目的平均收益率为π0且有π0≥r0。现面临一新项目，需要最低投资或企业预计投资为I，预期收益率为π1。企业的公司所得税率为T，当前面临的贷款利率为r1，且有π1≥r1。新项目有产出后，企业的息税前利润为Vπ0+ Iπ1。

2.4.1　无负债企业的融资权衡模型

表2.2　新项目有产出后，无负债企业在不同的融资方式下的利润分割情况

注：①股权融资全部为新股东提供；②企业无负债时V = S。

从上表可知，负债融资方式使得企业股东比在其他两种融资方式下少瓜分了Ir1（1 - T），但股权融资方式又会产生股权稀释作用，表现为原有股东只能获得息税后利润的V/V+I。

由于内部融资下原有股东收益都大于负债融资和股权融资时的原有股东收益，所以企业在拥有足够的自有资金时，必然趋向于内部融资。

当企业需要对外融资时，若决定负债，则要求其带来的原有股东收益不低于股权融资时原有股东收益，即：（Vπ0+ Iπ1- Ir1）（1 - T）≥（Vπ0+ Iπ1）（1 - T）V/V+I

整理得：I≥V（r1-π0）/π1- r1

表明只有当项目的最低投资或企业预计投资额达到一定规模时，企业才会负债融资。若π0≥r1，即企业原有项目的收益率高于现行贷款利率，仍保持较好效益的情况下，企业必然负债融资。企业原有项目效益较好，新股东凭借对新项目的投资而对原有项目利润的瓜分就多，即股票增发所带来的股权稀释作用较大，这是原有股东不情愿看到的。同时，留存在企业的付息后利润也较多，负债对股东的负税盾效应不显著。反之，若π0≤r1，即企业在走下坡路的情况下，则要求项目达到一定规模，使得股票增发所带来的股权稀释作用较大时才会负债融资。同时，由于企业原有项目的收益率低于现行贷款利率，导致留存在企业的付息后利润也较多，负债对股东的负税盾效应显著。而且新项目预期收益π1和原有项目效益π0越低，现行贷款利率r1越高，要求的项目投资规模就越大。

从股票收益率来看，负债融资导致的股票收益率应不低于股权融资导致的股票收益率，即：

两种融资方式下股票收益率的变化如图2.4所示（假定π0≤r1）：

其中，

由此可见，在投资规模达到之前，股票增发带来的股权稀释作用并不显著，股权融资的股票收益率PS大于负债融资的股票收益率PB，企业宜采取股权融资方式。只有当投资规模超过I*时，负债融资的股票收益率PB才大于股权融资的股票收益率PS，企业也因此宜采取负债融资方式。

图2.4　无负债企业融资权衡模型

2.4.2　负债企业的融资权衡模型

表2.3　新项目有产出后，负债企业在不同的融资方式下的利润分割情况

同无负债企业的分析一样，负债企业在拥有足够的自有资金时，必然趋向于内部融资。若需对外融资，企业负债融资的条件是：

整理得：

若Sr1+ Br0- Vπ0≤0即π0≥，企业原有项目效益仍然较好，则企业必然倾向于负债融资。与无负债企业相比，在银根紧缩利率上浮（r1≥r0）的情况下，负债企业必然倾向于负债融资所要求的原有项目效益低于无负债企业。而在银根放松利率下跌（r1≤r0）的情况下，负债企业所要求的原有项目效益则高于无负债企业。若，企业在走下坡路的情况下，则要求项目达到一定规模时才会负债融资。与无负债企业相比，在银根紧缩利率上浮（r1≥r0）的情况下，企业负债融资所要求的投资规模低于无负债企业。而在银根放松利率下跌（r1≤r0）的情况下，所要求的投资规模则高于无负债企业。而且新项目预期收益π1和原有项目效益π0越低，原有贷款利率r0和现行贷款利率r1越高，要求的项目投资规模就越大。

从股票收益率来看，负债融资导致的股票收益率应不低于股权融资导致的股票收益率，即：

令负债融资的股票收益率

股权融资的股票收益率

见图2.5。

图2.5　负债企业融资权衡模型

其中，由此可见只有当投资规模超过时，负债融资的股票收益率PB1才大于股权融资的股票收益率PS1，企业也因此采取负债融资方式。

【注释】

[1]类似于费方域对Hart（1995）专著的译法，对于我们考虑的公司制企业，我们把股东或所有者权益（Equity）译为股权，对权益资本与股权资本或股权融资不加区别。与之相对应的称为债务资本。

[2]这两个法则有时是有冲突的，即当现金流量超过两期时，投资回报率可能有多解，从而无法判断，一般净现值法始终是成立的。因此，本书只考虑净现值法，而不考虑其他投资法则，如投资回收期等。

[3]McCownell and Muscarella（1985）进行了这方面的实证分析，结果发现与理论暗示一致，他们选择样本是以1975～1981年间共658家公司，发现宣布预算增加的企业导致股价上涨（超过市场）约1%，而宣布预算减少的企业股价下降（与市场相比）1%以上。

[4]见Copeland and Weston（1986），125页。

[5]在式（2.17）、（2.18）、（2.19）中的Kb、ρ、Ks前加上期望算子E表示预期值或平均值，因为在MM定义中，未考虑风险，从而不存在不确定性，因而无需加E。

[6]在MM定义中，Ks=ρ+（ρ- Kb）（1 -τc）B/S中的Ks，ρ均是确定性变量，非随机变量，当推导式（2.20）时，我们实际上是把EKs，Eρ等代入上述方程，从而得到βL与βU的关系式，这里的Ks、ρ与CAPM中定义的区别是一个为确定性的，一个为随机的，之所以取同样的符号，主要是考虑便于比较。

[7]由于布莱克在一年前不幸去世，因而经济学方面的最高荣誉未能授予他，不过默顿与舒尔斯的获奖也说明布莱克的工作事实上也得到了诺贝尔经济学奖。

[8]默顿（Merton，1974）假定的随机微分方程为dV =（αV - C）dt +σVdz，其中C为单位时间里支付给股东的股利或支付给债权人的利息，C可以为负值，当C为负值时表明企业增加融资。因为这是一个连续时间（Continuous- time）方程，如α与σ写成t的函数，则会增加讨论难度，为简单起见，这里设为常数。

[9]式（2.25）与式（2.16）的区别是式（2.16）仅是一期模型，而式（2.25）考虑的是连续时间模型，因此（2.25）中变量用小写，另外由于是连续模型，rf在不同时点可以不同，但假定不是随机变量，因而为非随机回报率。

[10]式（2.35）类似于在CAPM中得到的式（2.20）只不过这里是连续时间模型，因而我们未用前面的记号βL与βU，实际是一样的，但两式给出的表达式并不一样。

[11]风险资本是指为一家新或年轻公司提供的股权资本，特别是指对高技术（High- tech）投资，一般风险很高，因而这类企业难以进行债务融资。风险投资公司是风险资本的主要提供者，如美国的ARD（American Research and Development）公司通过对美国数字设备公司（Digital Equipment Company即DEC）的风险投资取得巨大成功，引发了美国的风险投资热潮。

[12]这部分内容已在《预测》，1999（4）上发表。

[13]实际上，在MM公式与Miles-Ezzell公式中，均是用T*即单位利息支付所扣除的净税节约，在使用这些公式时，由于T*很难确定，故常用边际公司税率τc代替。

[14]Er*不能写成CAPM形式，即Rf+［E（Rm）- Rf］βr*形式，而在τc = 0或L = 0时，上述CAPM形式均可得到。τc = 0在时，由于企业股权资本与债务资本除风险系数不同外，其他无差异（这里未考虑），从而r*可看成是两资产的复合，但在τc≠0时，两者之差还有税赋效应，从而不能复合得到r*。当然L = 0时，全部为股权资本，可以直接运用CAPM。