探索重力与动能相互转化的麦克斯韦摆实验

麦克斯韦摆

Maxwell Rolling Pendulum

神舟五号发射成功以来，人们对超重和失重现象表现出很大的兴趣，但以往研究失重和超重的实验往往只做一些向上或向下的直线运动，而宇宙飞船、人造卫星在飞行过程中既有直线运动又有曲线运动，并且绝大多数是圆周和旋转运动。麦克斯韦摆既有上下运动又有旋转运动，摆轮在运动过程中失重和超重现象都会出现，于是人们利用麦克斯韦摆的实验原理设计了一种可以模拟宇宙飞船和人造卫星的、带有旋转运动的“失重和超重现象实验仪”。

实验装置

麦克斯韦摆的演示装置如图1和图2，支架上端系两根绳子，分别绕在一个圆盘状摆轮转轴的两端，摆轮可以绕轴转动。

图1　麦克斯韦摆实验装置

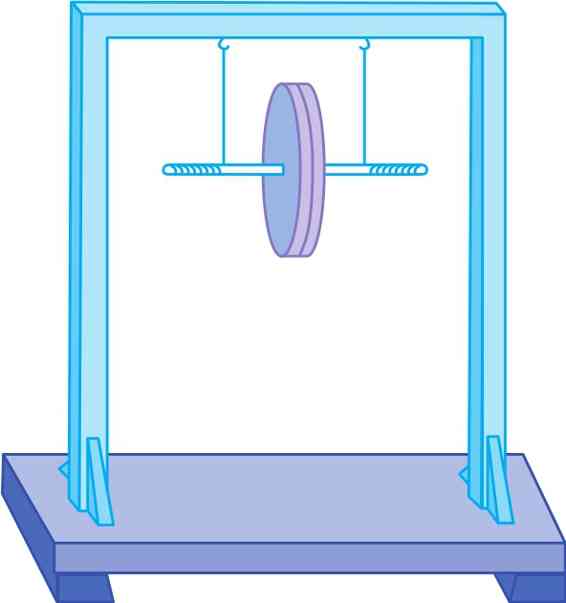
图2　麦克斯韦摆实验装置示意图

现象观察

1.调节绳子长度，使摆轮的转轴处于水平状态。

2.用手转动摆轮的轴，使摆轮上升到较高位置，同时使悬线均匀绕在轴上（绕线不能重叠）。

3.手松开后，摆轮自动旋转下降，并且越转越快。

4.在重力作用下，摆轮的重力势能转化为转动动能和平动动能，下降到最低点时，摆轮的转速最大，转动动能最大，势能最小。

5.当悬线完全伸开时，摆轮就不再下降。之后，它开始反向卷绕悬线上升，转动动能转化为重力势能和平动动能，摆轮的转速减小，位置升高，达到最高点后又会下落，如此上下往复运动。

现象解密

麦克斯韦摆是一种用来演示重力势能与动能的相互转化过程中，机械能总量保持不变的装置。如果忽略摆线与摆轴之间的摩擦力及空气阻力，摆在上下滚动过程中，每次上升的高度都相同，摆的重力势能与转动动能及平动动能相互转换，总的机械能守恒。

在重力作用下，摆轮的运动是质心的平动与绕质心的转动的叠加，其动力学过程可用牛顿第二定律和刚体转动定律来计算。摆轮的受力如图3所示。

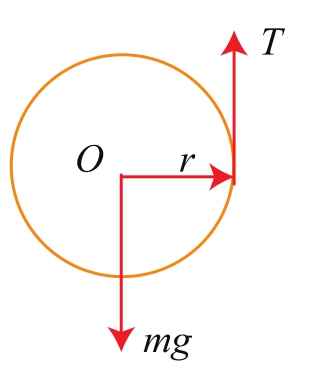
图3　摆轮运动过程中的受力情况

其动力学方程组如下：

解得

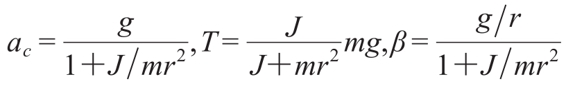(www.xing528.com)

于是，当摆轮从静止开始下落高度h后，有：

（1）质心平动动能为

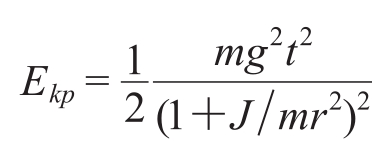
（2）绕质心转动动能为

（3）总动能为

由此可知，在摆轮向下滚动的过程中，重力势能逐渐减少，转变成了摆轮质心的平动动能与绕质心的转动动能；在摆轮上升过程中，平动动能与绕质心的转动动能逐渐减少，重力势能逐渐增加，总机械能不变。摆轮每次上升的高度相同，说明机械能守恒。

应用拓展

1.摆轮向下运动过程中，处于失重状态

在摆轮由最高点下降的过程中，假设摆轮向顺时针方向转动，其角速度越来越大，质心向下的速度也越来越大，质心的加速度a的方向向下，由mg－T=ma可知，T=mg－ma<mg，物体处于失重状态。

2.摆轮达到最低点时，处于超重状态

当摆轮达到最低点时，摆的悬线通过摆的轴心，此时摆仍然按顺时针方向转动，质心竖直方向下的速度突然降为零，质心的速度变为水平方向，因此必存在向上的加速度和向心加速度。由T－mg=ma－ma′可知，T=mg+ma－ma′>mg，可见物体处于超重状态。

3.摆轮向下运动过程中，处于失重状态

当摆轮按顺时针方向转动着向上运动时，转动的角速度越来越小，质心的速度也越来越慢，即加速度为负（假定向下为正方向），T=mg－ma<mg，可见物体处于失重状态。

4.摆轮在最高点，应该处于既不失重也不超重的状态

思考题

1.分析摆轮下落速度(平动)与位置高度的关系。

2.分析摆轮上下平动的周期与轴径的关系。

3.分析摆轮上下平动的周期与摆轮质量的关系。

4.分析摆轮上下平动的周期与摆轮转动惯量的关系。

5.观察摆轮转速随高度的变化情况，并分析原因。

6.摆轮经多次上下往复运动后，爬升高度越来越低，这是什么原因？