大米和玻璃瓶的机械能守恒研究

物态和惯性

Matter State and its Inertia

牛顿第一定律认为惯性是物体的固有性质，物体惯性的大小由其质量决定，而与运动状态无关。那么惯性是否与物体的存在形态，即固态、液态等有关呢？

实验装置

两个相同的圆柱形透明玻璃瓶、大米、一片黄色塑料膜、一块光滑木板等。

现象观察

称出玻璃瓶质量，其中一个玻璃瓶中灌满大米（尽可能多装），另一个玻璃瓶中装有相同质量的水。将两个圆柱形玻璃瓶放在木板斜面上的同一高度，让它们同时滚下（如图1所示），观察哪个玻璃瓶滚得快、滚得远。

两玻璃瓶同时释放后，观察到在斜面上，装水的玻璃瓶滚得快（如图2所示），但到了地面上滚动一段距离后，发现装大米的玻璃瓶滚动速度会超过装水的玻璃瓶，最终装大米的玻璃瓶滚得更远。

图1　两玻璃瓶同时释放

图2　两玻璃瓶下滚过程

现象解密

上述分别装有大米与水，但总质量相同的玻璃瓶，它们的滚动情况是否说明相同质量的物体运动状态的改变与物体的存在形态有关呢？我们分别对以上两种情况进行定量分析。从实验观察发现，两个玻璃瓶都没有明显的滑动，因而假设它们都做纯滚动。

1.装大米的玻璃瓶

玻璃瓶在下滚的过程中，我们发现玻璃瓶中的大米与玻璃瓶没有相对运动，而是一起滚动下来的。如图3所示，设玻璃瓶与大米的总质量为M，沿斜面下滑某一瞬时速度为v。由于大米被完全挤压在一起，大米与玻璃瓶就相当于是一个实心圆柱体，其纵向轴转动惯量为Ι₁，瞬时转动的角速度为ω，g为重力加速度，h为斜面的高度。玻璃瓶下滚的过程中机械能守恒，得运动方程为(www.xing528.com)

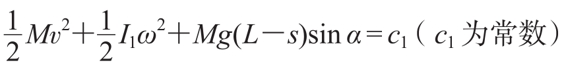
玻璃瓶转速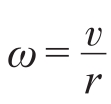，设玻璃瓶与大米总的转动惯量为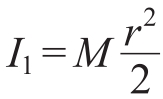。则上述运动方程可化为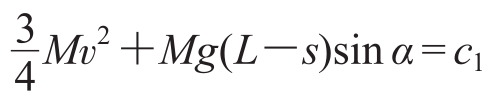（r为两个玻璃瓶的半径），运动方程对时间求导之后，得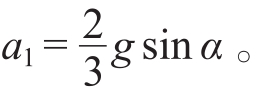

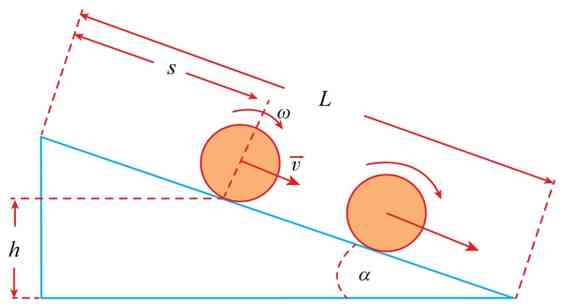
图3　实心圆柱体斜面上下滚示意图

2.装水的玻璃瓶

透过玻璃瓶，我们发现虽然玻璃瓶是滚下来的，但是瓶中的水开始时并未旋转滚动（为便于观察，本实验中瓶内放入了黄色塑料膜）。玻璃瓶中的水只是沿斜面向下滑动。设透明玻璃瓶的质量为m，玻璃瓶与水的总质量为M。一个空心玻璃瓶绕纵向轴旋转惯量I₂=mr²,ω=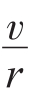,m=kM,k<1。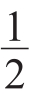Mv²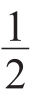＋I₂ω²＋Mg(L－s)sinα=c₂,c₂为常数。将I₂=mr²,ω=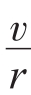,m=kM代入，得

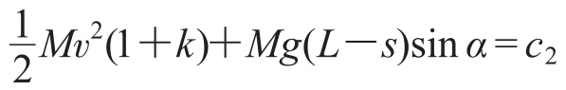
对运动方程时间求导，得a₂=gsinα⋅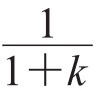。我们发现刚开始时，装水的玻璃瓶比装大米的玻璃瓶滚得快，即a₁<a₂，则需要满足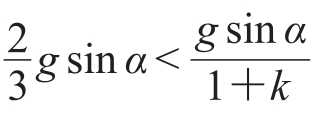，得k<。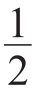

根据测量值：M=554.8g,m=96g,k=0.173。所以，装水的玻璃瓶开始滚动时的角加速度较大，滚得自然较快。

但在下滚以及在平面上滚动的整个过程中，装大米的玻璃瓶由于米与玻璃瓶之间没有相对运动，可看作为一个刚体，在斜面上势能转化为动能，在水平面上，动能全部转化为克服与地面间的摩擦力所做的功。而装水的玻璃瓶中由于水与玻璃瓶之间有相对运动，存在摩擦，在整个运动过程中，玻璃瓶会带动水而使水逐步转动，因而内部就会消耗能量，故在水平面上滚动距离就短。

应用拓展

相同的玻璃瓶，如果一个玻璃瓶里装满大米，而另一个玻璃瓶里没有装满大米，则它们的运动情况又如何？哪个先到达最低点，哪个在水平地面上滚得较远呢？

思考题

1.如何辨别一个鸡蛋是生的还是熟的？

2.你能否想象油罐车内部的结构是怎样的？