基于支持向量机预测结构疲劳寿命

疲劳机理研究已表明塑性变形是造成材料损伤的基本因素，损伤随着载荷历程的推进不断累积，疲劳破坏就是材料性能在载荷作用下不断劣化的过程。

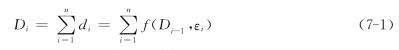
损伤的累积具有非线性特点，某个时刻造成的损伤是由此时的损伤状态、所受的载荷循环所决定的，从而可在某一瞬时状态的总损伤量、所受的循环应力／应变幅与所造成的损伤量之间建立非线性映射关系，如下式所示：式中Di为第i次循环后材料的累积总损伤；εi为第i次循环载荷幅；di为该循环载荷造成的损伤。经过n次循环载荷作用后，累积损伤D达到临界值时，材料发生疲劳破坏，循环数n乘以载荷作用次数便可获得疲劳寿命。

但由于疲劳损伤机理的复杂性，很难用特定的数学表达式来准确描述疲劳损伤累积与载荷之间的非线性关系。本书尝试利用支持向量机算法建立损伤量和载荷之间的关系，即以载荷和损伤累积参量作为输入层，以单次损伤量作为输出层，建立它们之间的映射关系，如图7－1所示。

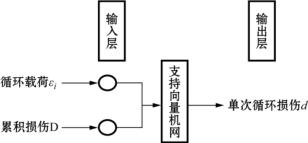
图7－1　损伤计算示意图

基于支持向量机的单轴疲劳寿命预测方法主要包括以下步骤：

1）收集材料疲劳性能数据

进行材料疲劳特性实验或通过查阅资料，收集相关数据，获取建立训练样本所需的各种材料性能参数。

2）选择合适的输入输出参数，建立训练样本集

对于不同的材料疲劳损伤机理，选取不同的输入输出参数，应用不同的损伤公式计算单次循环载荷损伤。

（1）对于以应力为控制参量的疲劳模型，选取循环载荷应力、当前累积总损伤作为输入参数，以单次循环载荷造成的损伤作为输出参数。通过比较几种损伤模型，通过能量法来计算单次循环损伤。

能量法以材料的应力－应变滞回环曲线为基础，认为塑性功的累积产生材料不可逆损伤从而导致疲劳破坏，对载荷应力级别、材料的循环软化硬化特性和载荷顺序进行综合分析，能够较准确反映材料性能变化和实际损伤过程。其损伤计算公式为

式中Δwj为第j次载荷循环作用下应力－应变滞回环曲线所对应的塑性应变能；Δwfj为第j次载荷循环应力级σf下材料的疲劳韧性。

（2）对于以应变为控制参量的疲劳模型，选取循环载荷应变、当前累积总损伤作为输入参数，以单次循环载荷造成的损伤作为输出参数。单次循环损伤通过Landgraf公式来计算。(www.xing528.com)

Landgraf公式认为在整个疲劳过程中弹性应变和塑性应变同时起作用，疲劳损伤应由塑性应变εp和弹性应变εe的比值来控制，同时考虑了平均应力的影响。其损伤计算公式为

式中σ′f为疲劳强度系数；E为弹性模量；ε′f为疲劳延性系数；b为疲劳强度指数；c为疲劳延性指数。

将材料疲劳性能数据，代入上述公式计算后，就可得到不同载荷级别下、不同的疲劳累积总损伤与单次循环载荷损伤的对应关系，构建训练样本集。

3）建立基于支持向量机的疲劳寿命预测网络模型

将训练样本输入到支持向量机中，通过计算，建立基于支持向量机的疲劳损伤计算模型。

为了提高支持向量机算法的计算精度，需要选择合适的核函数。一般常用的核函数有线性核函数、多项式核函数以及径向基核函数等，通过计算发现采取径向基函数能够取得较好的预测效果。径向基函数参数的选择，利用交叉检验方法自动寻优得到。

4）疲劳载荷谱预处理

疲劳破坏过程中，外部载荷对材料的作用是连续的。在输入到寿命预测模型前，须对结构所受疲劳载荷进行预处理。采用局部应力－应变法，将疲劳载荷谱转换为名义应力－时间历程，利用材料的循环应力－应变滞回曲线和Neuber方程转换为疲劳寿命预测模型所需的载荷输入参数类型。

5）计算疲劳寿命

按载荷循环－时间历程，将载荷参数逐次代入到基于支持向量机的疲劳损伤计算模型中，即可计算出对应不同载荷、不同的累积总损伤下单次循环载荷造成的疲劳损伤。通过不断的迭代计算，当累积损伤达到临界损伤值时，即判断发生疲劳破坏，计算载荷循环数，得到疲劳寿命值。

具体流程如图7－2所示。

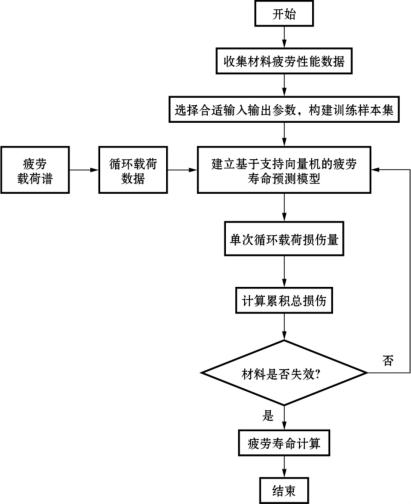
图7－2　疲劳寿命预测流程图