振动测试法简支梁损伤识别算例

本节采用文献［34］中通过实验测得的矩形钢梁损伤数据，以模态频率作为损伤标志量，利用基于支持向量机的损伤分步识别方法实现对简支梁损伤位置和损伤程度的识别，并与三层后馈式神经网络方法（Back－propagation Neural Network，BPNN）的计算结果作比较。

1）简支梁模型

简支矩形钢梁如图4－2所示。长L为0．8m，宽b为0．01m，高h为0．06m。弹性模量E为2．1×1011Pa，剪切模量G为7．65×108Pa，泊松比ν为0．28，密度ρ 为7．8×103kg／m3。

图4－2　矩形截面梁模型

在矩形截面梁的100mm、200mm、300mm、400mm的地方，分别锯开深度为10mm、15mm、20mm、30mm，宽为0．14mm的缺口。以此16个损伤情况下简支梁的前5阶固有频率作为训练样本。

将另外5个裂纹简支梁的前五阶固有频率作为测试样本，如表4－2所示。

表4－2　简支梁损伤识别测试样本

为保证收敛，对样本数据进行归一化处理。(www.xing528.com)

2）简支梁损伤识别结果

表4－3和表4－4分别为简支梁损伤位置和损伤程度的计算结果。

从表4－3可以看出，使用神经网络进行损伤位置预测的误差较大，绝对误差最大达到了26．7mm，最小也有5mm。而基于支持向量机的分步识别方法的误差较小，绝对误差最大为10．03mm，最小仅为1．83mm，相对预测误差控制在5%以内。分步识别方法的损伤识别效果明显好于神经网络。

对损伤程度的识别结果也说明了这一点。从表4－4可以看出，神经网络的损伤程度预测误差较大，绝对误差最大接近4mm，相对误差达到31．88%。基于支持向量机的损伤分步识别结果是令人满意的。绝对误差均小于1mm，最小仅为0．06mm。

从对简支梁的识别结果可以看出：基于支持向量机的损伤分步识别方法比神经网络方法的计算精度有了显著提高。

表4－3　简支梁损伤位置识别结果

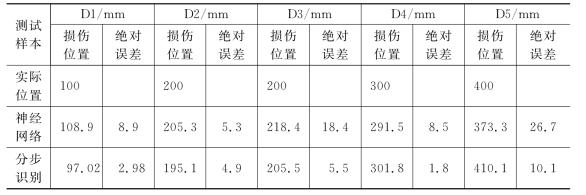
表4－4　简支梁损伤程度识别结果