悬臂梁仿真计算及结构损伤识别方法研究

选取悬臂梁作为仿真算例，选用频率与曲率模态作为特征参数检验基于支持向量机的损伤分步识别方法的可靠性。

1）悬臂梁模型

选取一等截面无阻尼悬臂梁作为仿真算例，其长L、宽b、高h分别为0．4m、0．003m和0．04m，弹性模量E为2．1×1011Pa，泊松比ν为0．28，密度ρ为7．8×103kg／m3。

仿真计算使用有限元软件ANSYS 7．1，通过计算比较后发现使用二维单元即可满足计算要求，所以单元类型选用SHELL63，将梁分割为48个单元，共51个节点。梁损伤发生时，通过损伤发生处两边长为5mm、高为40mm范围内单元弹性模量的下降进行模拟，单元弹性模量不同的下降百分比模拟不同的损伤程度。

以频率参数和曲率模态参数一起构成损伤特征量，反映了结构整体特性和局部特性，可以提高损伤诊断的精度。另外，在计算前一般需要对模态参数进行预处理，进行归一化处理。

曲率模态振型通过中心差分法近似计算得到。当测点为等间距h布置时，曲率可由下式计算：

式中 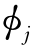（i）为第j阶振型第i测点的位移值。

2）构造训练集和测试集

选取悬臂梁中心线上17个节点的曲率模态参数进行计算。为了提高计算精度，选择损伤发生时前三阶频率、曲率模态的最大变化量和相应的节点位置共7个参数作为输入向量。

以60mm、140mm、220mm和300mm处分别发生从10%到70%的不同损伤程度共28个损伤样本作为训练集，构造支持向量机损伤识别网络。为了检验识别效果，另以100mm、180mm、260mm和320mm处分别发生从10%到70%的损伤共28个样本作为测试集。选取320mm处的损伤是为了检验损伤识别方法的外推效果，其余测试样本是检验其内推效果。(www.xing528.com)

3）悬臂梁损伤识别结果

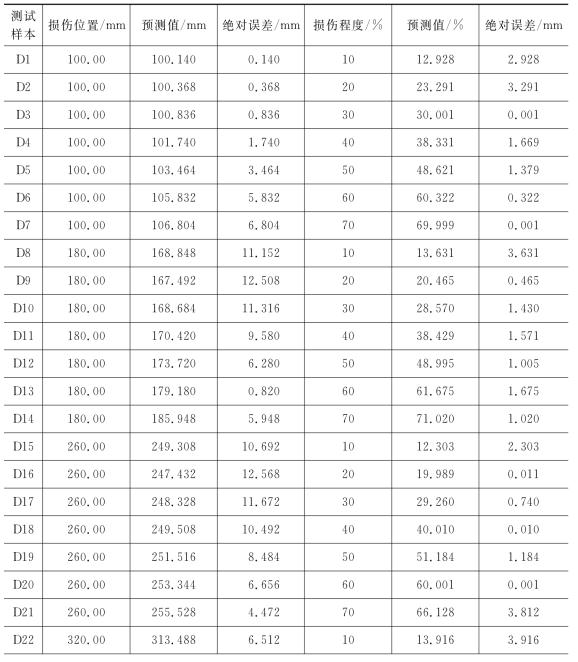
将训练样本按损伤位置分为4类，计算后形成支持向量机损伤位置分类模型，28个测试样本输入计算后得到分别属于这4类的概率分布。考虑到训练样本分类数较少，每个测试样本各自选取对应分类概率最高的2～3个类样本分别构成新的训练样本，进行支持向量机回归计算。表4－1为所有测试样本损伤定位和程度估计的结果。

以D1测试样本为例，属于4类损伤位置的分类概率分别为38．64%、48．38%、6．89%和6．09%；于是选择前两类即在60mm、140mm处的损伤样本重新组成训练样本，使用支持向量机回归算法计算，损伤位置的预测值为100．140mm。

从表4－1可以看出，损伤定位绝对误差从0．140mm到13．692mm，平均误差为6．404mm；而相对误差最大为7．307%，不超过10%。在100mm处的预测效果最好，平均误差为2．741mm。损伤定位内推的平均误差为6．991mm；而320mm处的识别结果平均误差为4．643mm，相对误差为1．451%，外推效果好于内推。

表4－1　悬臂梁损伤分步识别算法计算结果

（续表）

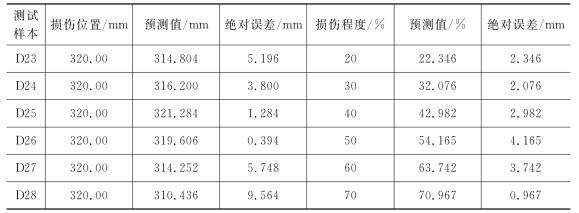
对于损伤程度的预测，绝对误差在5mm以内，最小为0．001mm，最大为4．165mm；而相对误差变化较大，最大达到36．31%，最大值均出现在损伤程度为10%处。同时相对误差有随着损伤程度增加而预测值精度逐步提高的趋势，发生较小程度的损伤时较难精确预测。

总体看来，分步识别方法对于悬臂梁的损伤信息预测是比较满意的。