简支梁仿真计算成果-基于振动测试的结构损伤识别若干方法研究

选择一等截面无阻尼简支梁作为数值计算模型。该简支梁的截面特性为：长度l＝1m，高度h＝0．04m，宽度b＝0．01m，弹性模量E＝210GPa，密度ρ＝7 800kg／m3。假设在简支梁位置xd＝0．3l处发生程度为ε＝0．2的裂纹损伤，裂纹宽度为Δl＝0．01l。

根据第2章采用二阶摄动法的计算可得：无损梁的第一阶固有频率为94．11Hz，发生损伤后频率降低为93．99Hz。可以看出损伤前后频率变化较小，单纯靠频率来检测损伤是否发生比较困难。下面利用基于小波分析和HHT变换的检测方法，分析简支梁加速度响应信号来判断损伤的出现。

在简支梁中间位置进行激励，激励信号为正弦信号10sin（60t），并在梁中间位置采样加速度响应信号，响应时间取1s，采样频率取100Hz。

首先对响应信号进行小波分解，通过计算比较后发现dB2小波基对响应信号分解效果较好，所以使用dB2小波基将原始信号作小波包二层分解，然后对4个小波分解子信号进行经验模式分解，得到各自的IMF分量。将IMF分量与原分解子信号作相关分析，取最大相关系数的1／15作为筛选标准，凡是相关系数大于或者等于筛选标准，该IMF分量就保留，否则加入到剩余分量中，接着计算各IMF分量的瞬时频率和瞬时幅值图。

同时，为了便于分析和简化计算，对IMF分量的瞬时频率在［0，0．5］之间进行归一化处理。

图3－2～图3－5描述了无损简支梁和裂纹简支梁各自加速度信号第一个小波分解信号的计算过程。

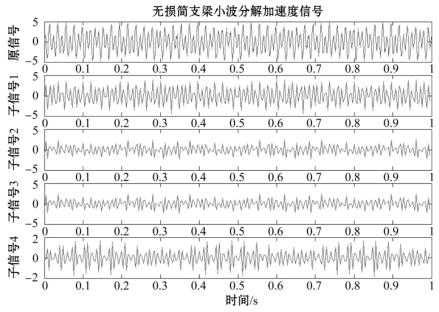
图3－2　无损简支梁加速度信号及其小波包二层分解结果（m／s2）

图3－3　无损简支梁加速度信号第一个小波分解信号的EMD分解示意图

图3－4　裂纹简支梁加速度信号及其小波二层分解结果（m／s2）

图3－5　裂纹简支梁加速度信号第一个小波分解信号的EMD分解示意图

图3－6～图3－13分别比较了损伤前后简支梁加速度信号从第一个到第四个小波分解信号IMF分量的时间－瞬时频率、时间－瞬时振幅对比图。

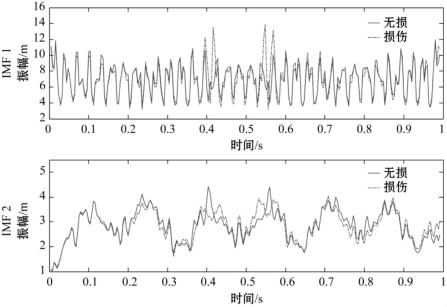
图3－6　损伤前后简支梁加速度信号
第一个小波分解信号IMF分量的时间－瞬时振幅对比图

图3－7　损伤前后简支梁加速度信号
第一个小波分解信号IMF分量的时间－瞬时频率对比图 (www.xing528.com)

图3－8　损伤前后简支梁加速度信号
第二个小波分解信号IMF分量的时间－瞬时振幅对比图

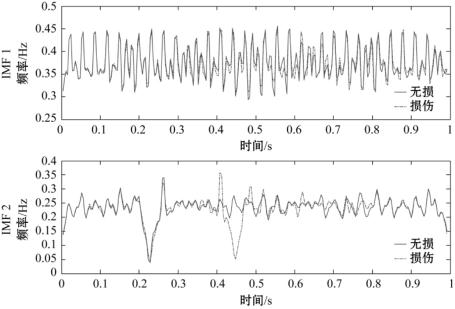
图3－9　损伤前后简支梁加速度信号
第二个小波分解信号IMF分量的时间－瞬时频率对比图

图3－10　损伤前后简支梁加速度信号
第三个小波分解信号IMF分量的时间－瞬时振幅对比图

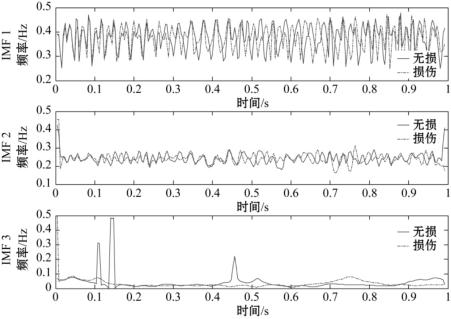
图3－11　损伤前后简支梁加速度信号
第三个小波分解信号IMF分量的时间－瞬时频率对比图

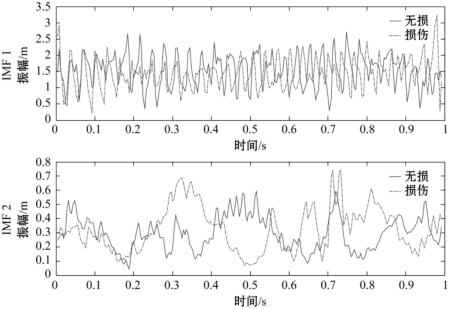
图3－12　损伤前后简支梁加速度信号
第四个小波分解信号IMF分量的时间－瞬时振幅对比图

图3－13　损伤前后简支梁加速度信号
第四个小波分解信号IMF分量的时间－瞬时频率对比图

从损伤前后IMF分量的时间－瞬时频率图、时间－瞬时振幅对比图可以得出以下结论：

（1）图3－6、图3－7分别是损伤前后第一个小波分解信号IMF分量的时间－瞬时振幅图和时间－瞬时频率对比图，可以看出IMF分量的瞬时频率和瞬时幅值都有明显的差异，特别是在时间0．4s和0．56s处。IMF 1的瞬时振幅在这两个时刻出现突增，增幅最高达到40%；而瞬时频率出现明显的下降，从损伤前的0．47，下降到0．08；IMF 2的瞬时频率也出现下降，从0．27降到0．14。

（2）图3－8和图3－9分别是损伤前后第二个小波分解信号IMF分量的时间－瞬时振幅图和时间－瞬时频率比较图。IMF 1分量的瞬时频率变化不明显，而瞬时振幅在（0．4s，0．5s）之间出现突增，但不如IMF 2分量的变化明显。损伤发生后IMF 2分量的瞬时振幅在约0．45s处出现了波峰，增幅达到了90%，而此时的瞬时频率则出现了比较明显的波谷。

（3）图3－10和图3－11则是损伤前后第三个小波分解信号IMF分量的时间－瞬时振幅图和时间－瞬时频率对比图。与无损伤信号相比，明显的变化发生在低频IMF 3分量中，瞬时频率在0．1s、0．45s处下降很明显，瞬时振幅则在0．45s、0．75s变化最明显。

（4）图3－12和图3－13分别是损伤前后第四个小波分解信号IMF分量的时间－瞬时振幅图和时间－瞬时频率图。从两图对比可以看出，信号变化在IMF 2分量在表现明显。损伤IMF 2的瞬时振幅在0．33s、0．5s、0．65s均有较大的波动，而瞬时频率图在这些位置也出现了不同程度的波峰和波谷。

从以上分析可以看出，损伤前后的简支梁加速度响应信号经过基于小波分析和HHT处理后，其IMF分量瞬时振幅图和瞬时频率图能够反映信号出现了较明显变化，从而利用该方法可以检测出简支梁损伤的发生。