选择一等截面无阻尼简支梁作为数值计算模型,该简支梁的截面特性为:长度l=1m,高度h=0.04m,宽度b=0.01m,弹性模量E=210GPa,密度ρ=7 800kg/m3。运用二阶摄动法计算损伤发生时的固有频率和模态振型,研究裂纹简支梁振动模态参数的变化规律。
1)裂纹简支梁频率变化特性
考虑到简支梁的结构对称性,选取损伤工况如下:在距简支梁端点0.1m、0.2m、0.3m、0.4m、0.5m处,分别发生程度为10%、30%、50%、70%的裂纹损伤,裂纹宽度为Δl=0.01l。
采用二阶摄动法公式计算简支梁第一至第四阶的固有频率,通过以上计算可以检验裂纹简支梁的各阶自振频率是如何随着裂纹深度和位置变化的。表2-1~表2-4分别是简支梁在不同损伤位置发生10%、30%、50%、70%程度损伤下第一阶到第四阶的固有频率,图2-3~图2-6分别是第一阶到第四阶的固有频率的变化曲线。这样对于给定的裂纹位置,可以得到固有频率与损伤程度的关系曲线;或者对于给定的损伤程度,可以得到固有频率与裂纹位置的关系曲线。
表2-1 不同损伤位置和程度下的简支梁第一阶固有频率
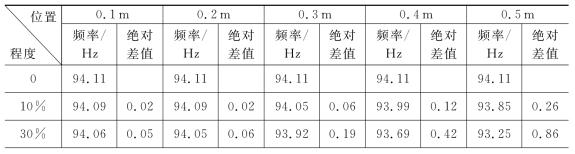
(续表)
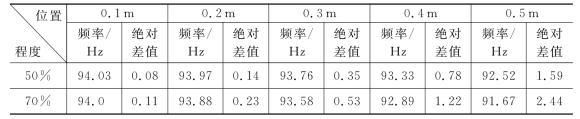
表2-2 不同损伤位置和程度下的简支梁第二阶固有频率
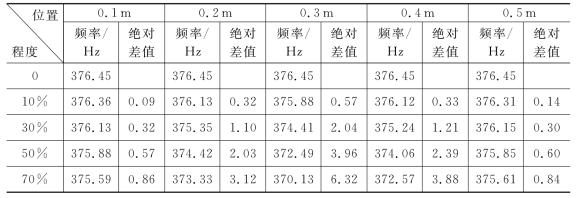
表2-3 不同损伤位置和程度下的简支梁第三阶固有频率
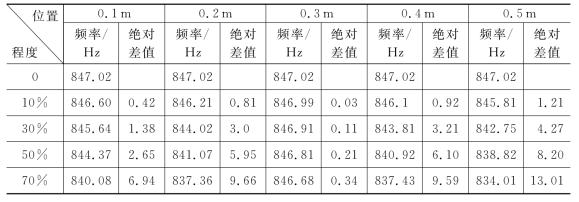
表2-4 不同损伤位置和程度下的裂纹简支梁第四阶固有频率
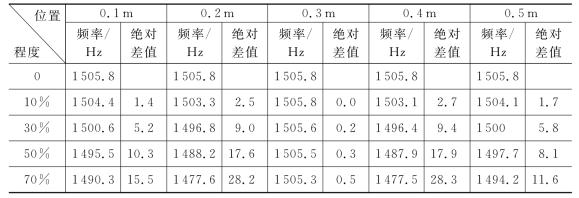
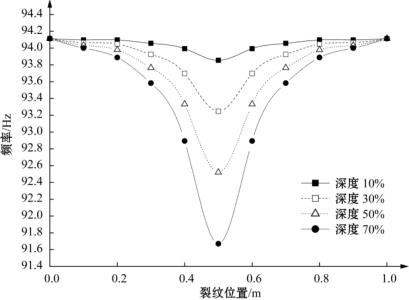
图2-3 裂纹简支梁第一阶固有频率变化示意图
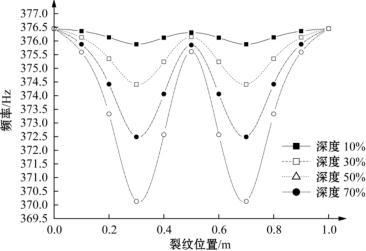
图2-4 裂纹简支梁第二阶固有频率变化示意图
从这些结果中可以发现以下一些现象:
(1)对于各阶振型而言,裂纹处于简支梁的支撑处时,频率与没有裂纹时相同;当裂纹位置固定时,频率随着裂纹深度的增加呈下降趋势。在一定情况下,固有频率的变动量与损伤程度成正比。
(2)对于第一阶振型,在裂纹深度一定的情况下,当裂纹从简支梁的左支撑处移动到简支梁的跨中时,固有频率呈降低的趋势;当裂纹从简支梁的跨中移动到简支梁的右支撑处时,频率呈上升的趋势,这充分体现了简支梁的对称特性。
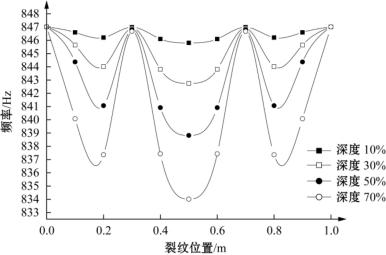
图2-5 裂纹简支梁第三阶固有频率变化示意图
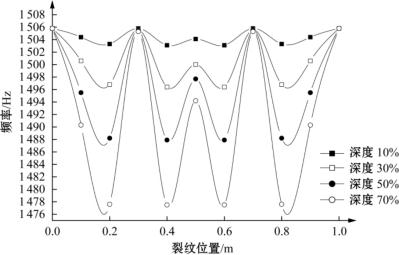
图2-6 裂纹简支梁第四阶固有频率变化示意图
(3)对于第二阶振型,当裂纹在跨中和两个支撑处时,频率相同。这是因为跨中恰好是第二阶振型的拐点(模态振型的第二阶导数等于零的点),裂纹在拐点处时对应的频率不发生改变。当裂纹从支撑处移动到简支梁的1/4处时,频率呈现降低的趋势;当裂纹从简支梁的1/4处移动到跨中时,频率呈上升的趋势。(https://www.xing528.com)
(4)对于第三至第四阶振型,除了裂纹在两个支撑处时频率与没有裂纹时相同外,中间还各有2~3个点处频率与没有裂纹时相同,这是因为对应的振型分别有2~3个拐点,裂纹在拐点处时对应的频率不发生改变。当裂纹从支撑处移动到相应振型第一个拐点的一半处时,对应振型的频率呈下降趋势,而当裂纹从相应振型第一个拐点的一半处移动到第一个拐点处时,对应振型的频率呈上升趋势。
(5)从计算结果可以看出,在微小损伤的条件下,相对于损伤前的固有频率,简支梁的频率变动量是比较小的。因此,存在测量噪声的条件下,如果单纯从结构的固有频率变化来识别微小的损伤,要获得正确的识别结果比较困难。
2)裂纹简支梁模态振型变化特性
以距左端0.4m处简支梁发生50%的损伤为例,研究裂纹损伤对第一阶到第四阶位移模态和曲率模态振型的影响。曲率是位移的二阶导数,对应于每一阶位移模态,则必有其对应的曲率分布状态。求解式(2-59)模态振型的二阶微分即可得到曲率模态振型。
图2-7是损伤前后的第一阶到第四阶简支梁位移振型图;图2-8则是第一阶到第四位移振型变化绝对值的示意图。
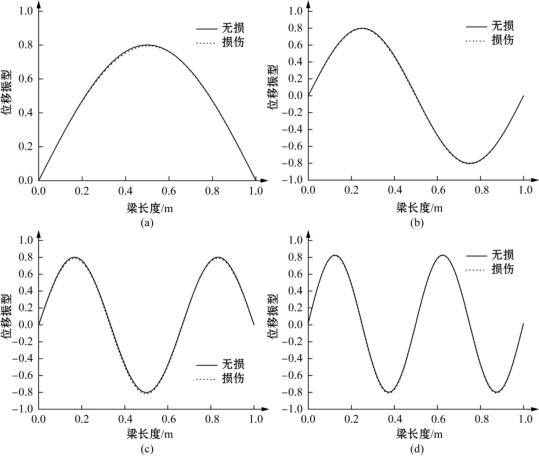
图2-7 损伤前后简支梁第一阶到第四阶位移振型示意图
(a)第一阶;(b)第二阶;(c)第三阶;(d)第四阶
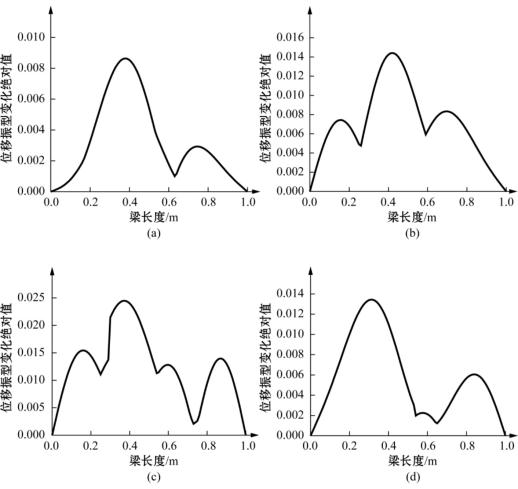
图2-8 损伤前后简支梁第一阶到第四阶位移振型变化绝对值示意图
(a)第一阶;(b)第二阶;(c)第三阶;(d)第四阶
图2-9是损伤前后的第一阶到第四阶简支梁曲率模态振型示意图;图2-10则是第一阶到第四位移曲率振型变化绝对值的示意图。
通过分析图2-7~图2-10的损伤前后位移振型和曲率振型的变化,可以得出以下结论:
(1)损伤的出现对简支梁位移振型和曲率振型都有影响,通过判断振型损伤前后振型变化最大的区域,可以判断出损伤发生的位置。
(2)损伤对各阶振型的影响程度不同。从图中可以看出,发生在0.4m处的损伤对第三阶振型的影响最大,而对第一阶振型的影响最小;第三阶位移振型变化的绝对值大约是第一阶的3倍,而曲率振型变化的绝对值更大,大约是第一阶振型变化的5倍。
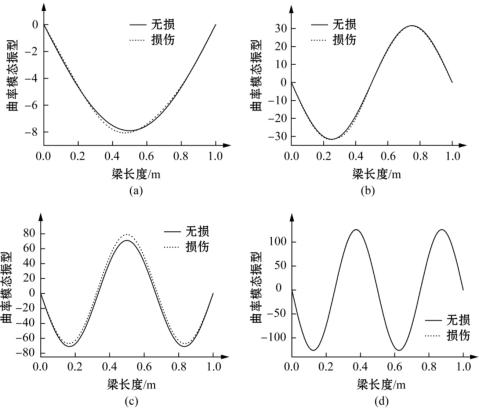
图2-9 损伤前后简支梁第一阶到第四阶曲率模态振型示意图
(a)第一阶;(b)第二阶;(c)第三阶;(d)第四阶
(3)同曲率振型相比,位移振型的变化并不很明显。在实际测量中考虑到噪声的影响,单纯使用位移振型来检测损伤比较困难。
(4)在损伤发生处,第一到第四阶曲率振型都发生了明显变化。而且每一阶曲率振型的变化值都是其对应位移振型变化的数十倍,曲率振型更能反映损伤对结构振动特性的影响。所以用曲率模态来识别梁的损伤,其效果要优于用位移振型。
(5)从振动特征方程的求解过程中可以看出,摄动法在计算过程中需要进行大量的循环迭代计算。在提高计算精度的同时,也将损伤区域处振型变化的影响扩展到整个振型上。从图中损伤前后模态振型的变化曲线也可以看出这一点,振型的变化呈波浪形,在损伤位置出现波峰。仅仅利用一阶振型来判断损伤位置有可能出现误判,最好利用二阶到三阶振型来对比分析。
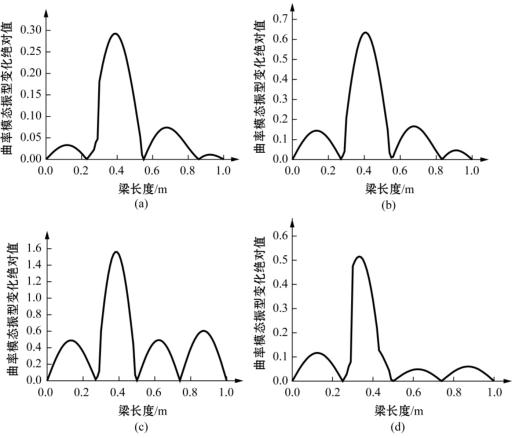
图2-10 损伤前后简支梁第一阶到第四阶曲率模态振型变化绝对值示意图
(a)第一阶;(b)第二阶;(c)第三阶;(d)第四阶
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




