多目标规划模型在煤炭工业生态产业链优化仿真研究中的应用

4.2.4　多目标规划模型

多目标决策问题的理论基础之一是向量优化问题，也称为多目标优化问题。这类问题，从方法论的角度看，它是一个目标函数中具有向量值的数学规划问题。从决策论角度看，它又是决策规则中含有各个目标极值的决策问题。因此，多目标决策问题属于向量优化问题。

向量优化问题的解与标量优化问题的解是不同的，多目标优化问题的解都是非劣解，且不是唯一的。非劣解的概念最早是由法国经济学家帕雷托于1896年提出来的，但是发展为向量优化问题的生成非劣解技术，还是在1951年Kuhn－Tucker非劣性条件发表以后。

（1）多目标规划的数学模型

式中：X＝（x₁，x₂，…，x_n）为决策变量。该式表示有m个约束条件，n个决策变量，p个目标函数的多目标规划模型。

其各种解定义如下：

绝对最优解：若对于任意的X，都有F（X＊）≥F（X）有效解：若不存在X，使得F（X＊）≤F（X）

弱有效解：若不存在X，使得F（X＊）＜F（X）

（2）多目标规划模型的求解方法

1）约束法。又称主要目标法，其基本思想是：在多个目标函数中选择一个最为重要和最为关键的目标，作为主要目标函数，其他目标处理为适当的约束条件。

　　　maxf_k（X）

容易证明，约束法求解问题（P₂）的最优解，其Kuhn－Tucker条件与问题（P₁）有效解的K－T条件一致。因此，约束法求得的解是有效解。

2）评价函数法。其基本思想是把多目标最优化问题转化为单目标最优化问题，即运用某种方法把多个目标函数转化为一个实函数目标函数，作为评价函数，对评价函数进行最优化求解。多属性效用理论是专门研究这样的实函数（效用函数）存在的条件和如何构造的问题。

假设决策者偏好可以用一个效用函数表示，最后方案的选取即可以按效用函数值来决定。虽然效用理论为决策分析提供了一种工具，但其应用由于以下两个原因受到了限制。

第一，很多情况下，决策者提供的偏好信息不足以确定效用函数，即不满足存在性条件。

第二，即使满足存在性的条件，也很难估计或构造一个实际问题的效用函数。

常见的评价函数法主要有线性加权函数、加权偏差函数、几何平均函数、费效比函数、功效系数函数等。

①理想点法。首先，找出各单目标问题的最优值为理想点：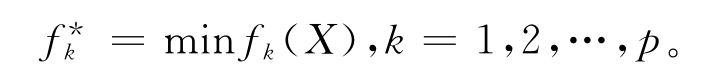

然后，构造令评价函数为：h（F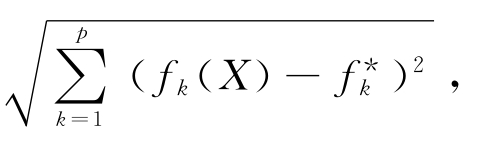）＝作为目标函数。

将多目标问题（P₁）转化为以下问题：(www.xing528.com)

　　minh（F（X））

　　s.t.g_i（X）≥0 i＝1，2，…，m。

②线性加权法。首先，给出每一目标f_k（X）的权系数λ_k，满足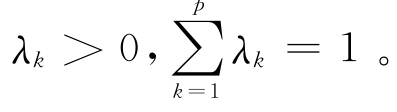

然后，取评价函数为h（F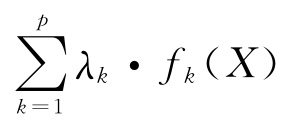）＝，作为目标函数，进行求解。

③平方和加权法。首先，求出各单目标问题最优值的下界f_k⁰（期望最好值）。

然后，取评价函数为h（F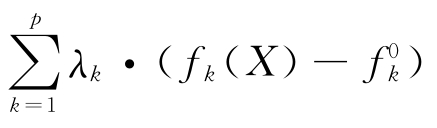）＝，作为目标函数，进行求解。

式中：λ_k为预先给定的f_k（X）的权系数，满足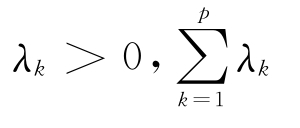＝1。

④“min－max”法。其基本思想是：在最不利的情况下找出最有利的策略。取各单目标函数的最大值来构造评价函数：h（F）＝maxf_k（X），然后求解下列规划问题：

3）交互式法。自20世纪80年代开始，用交互式方法求解多目标规划问题日趋广泛。本书在此介绍基于目标偏离容忍水平的交互式多目标决策方法，相比于其他交互式方法，此方法计算简单、交互快捷，同时又不影响结果的合理性。

交互式多目标决策方法的基本思想如下：第一，决策者在一定的科学依据下，结合实际情况提出各个目标的希望水平。第二，构造辅助模型，得到在给定目标希望水平下的非劣解，考察非劣解的相对目标偏离水平，如果各个目标的偏离水平在容忍限度之内，则得到满意解；否则，根据模型解及决策者偏好，调整一些目标的偏离容忍水平收紧或放松，继续求解。经过反复的交互过程，就可以得到不同偏好结构下的满意解。显然，构造恰当的辅助模型，解出合理的非劣解是决策的关键步骤。构造单目标辅助问题如下。 式中：F＊_i是A＊_i和B＊_i的通用形式，而A＊_i（或B＊_i）为目标A_i（x）［或B_i（x）］的希望水平；F_i′是A′_i和B′_i的通用形式，而A′_i（或B′_i）为目标A_i（x）［或B_i（x）］的容忍限度；同样，F＊_j是A＊_j和B＊_j的通用形式，F′_j是A′_j和B′_j的通用形式。W表示目标的允许值宽度；D表示目标F（x）的当前水平与希望水平之间的相对偏离。

在多目标问题的求解过程中，最重要的就是目标值的确定，太低，模型解将会出现“满意”但不优的状态，这肯定是不符合决策者意图的，基于目标偏离容忍水平的交互式多目标决策方法的特点在于用目标偏离容忍水平表示决策者偏好结构，因此确定目标希望水平可以遵循如下原则：尽可能取理想值作为目标希望水平值。为了向决策者提供其确定目标希望水平所需的信息，需对原多目标问题进行分解，求解各“个体最优解”。根据实际情况，决策者可以取尽可能趋近于个体最优解的目标函数值作为目标希望水平。实际上，很多情况下目标希望水平可以取与最佳可能水平相同的值。

根据以上分析，基于目标偏离容忍水平的多目标决策交互式方法的步骤如下。

第一：将多目标问题化解成单目标问题，并逐一求得其最优解。

第二：根据单一最优解来确定其最佳目标水平。

第三：建立辅助模型并求解。如有最优解，进入下一步。否则，原问题无非劣解，必须进一步考察原问题的模型结构和变量之间的关系，根据实际情况进行修正，然后转入第一步。

第四：如果决策者对辅助模型的最优解满意，则即为原问题的满意解，结束。否则，进入下一步。

第五：根据决策者的偏好结构，调整对不同目标的偏离容忍水平，构造新的辅助模型，求解。如有最优解，进入下一步。否则，根据实际情况修正目标偏离容忍水平，重复第五步。

第六：如果决策者对得到的最优解x′满意，则x′即为原问题的满意解，结束。

否则转入第五步。