中小学教师培训模式研究：提高教学质量

中小学教师教学质量评价方法研究

杜治汉

中小学教师教学质量评价一直是个热门而敏感的话题。说它热门，是因为教学质量评价随时都在进行，大到期中、期末考试，小到月考、单元测试，无一不要进行一番比较；说它敏感，是因为对一个教师教学质量的评价，直接关系到教师的人格尊严，甚至是教师的个人前途和命运。因此，如何科学合理地评价教师的教学质量，既是各级中小学领导迫切需要解决的现实问题，也是广大教师密切关注的焦点问题。

目前，中小学教师教学质量评价普遍采用的是静态评价方法，即按照本次考试学生的实际成绩，分班级、分层次，或者通过比较平均分，或者通过比较目标完成情况来决定谁优谁次。分层次比较的原因是因为教学是分层的。有些学校的管理者，为了便于比较，在学生人数本来不多的情况下，还是将每一层次的班额数设计为两个以上，“以便造成教师之间的竞争态势”，实际上也方便了管理。

但是，即便如此，很多教师对当前的评价方法仍颇有意见。其中一个重要原因就是没有考虑到学生基础不同带来的差异，尤其对于那些在毕业班才接手该班的教师来说，这种评价的不公正就显得更加突出。

鉴于此，本文提出了两种新的教学质量评价方法：其一是基于标准差的教学质量评价方法；其二是基于马尔柯夫链的教学质量评价方法。

一、基于标准差的教学质量评价方法

1．标准差

标准差是反映样本内各个数值与平均值差异大小的一个统计参数，从标准差可以了解样本内各变数的变异程度及样本平均数代表性可靠程度。标准差的表达式为s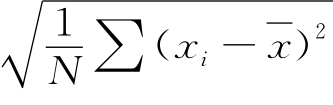＝，其中，N为样本数，x为样本总体的平均值，x_i为各个样本的观测值。由公式可见，当各个样本的观测值都相同时，x_i＝x，此时，标准差为零。因此，标准差描述的是样本的观测值与样本的平均值之间的总差距，标准差越大，说明各观测数值的变异程度越大，则平均值的代表性就越差。简单举例，如甲乙两班，每班各两人，某次考试成绩分别为：甲班｛60，60｝，乙班｛30，90｝，两班成绩平均值都是60，但甲班成绩标准差为零，而乙班成绩标准差大于零，其原因是乙班成绩差距很大。所以，在教师教学质量评价中，用标准差评价比用平均值评价具有更大的合理性。

2．标准差在教学质量评价中的应用

为了说明标准差评价的原理，我们不妨对实际情况作一简化。假设某年级有三个班，每班人数分别为2人、3人和4人，某次数学考试中他们成绩分别见表1。

表1　某年级三个班某次数学考试成绩

从平均分情况看，A班成绩最好，B班成绩最差，C班成绩居中。

下面考虑用标准差进行评价。

先计算年级平均成绩。简单计算得到年级的数学平均成绩是72分。

接下来利用上述数据计算各班的标准差。需要说明的是，标准差公式中平均值应取年级平均分，即x＝72．6。x_i取各班学生的实际成绩，N取各班的实际人数，如对A班，其标准差可计算为：

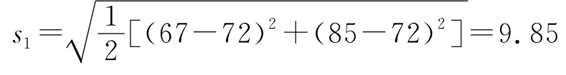
同理可计算B班和C班的标准差分别为：

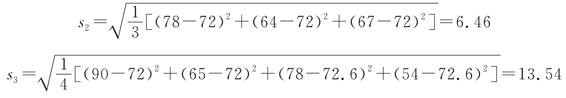
考虑到B班和C班平均成绩低于三个班级的平均成绩，因此将s₂和s₃分别取负值，即s₂＝-6．46，s₃＝-13．54。

那么，计算出的三个班标准差说明了什么呢？

由于标准差反映了样本内各个数值与平均值差异的大小（以平均值为参照，把平均值当成零），标准差越大，则说明距离平均值越远。因此，从数据可直观地看出，A班成绩高于平均分，是三个班中最好的；C班成绩不仅在平均值下，且距离平均值最远，因此，本次考试C班成绩最差，而B班居中。

这个评价结果与用平均成绩进行评价的结果是不完全一致的。哪种方法更科学一些呢？

观察一下B班和C班的成绩分布情况，可以发现，B班各成绩更多地分布在总平均分（72）附近，而C班成绩高低差别更大，最大差距达36分，或者可以理解为C班平均分高于B班，是因为少数学生作了较大贡献，但这并不代表总体成绩都好。

因此，标准差是从一个班级总体来考察教学质量的，其科学性显然要比仅用平均分进行教学质量评价更为科学合理。

但如果评价到此为止，也还不是十分科学，因为这种评价仍然是静态的，如果学生基础本来就不一样，那么其评价结果的真实性就值得怀疑了。

如何既考虑学生基础，又反映在此基础上学生学习状态的变化就是科学评价应解决的问题。

为此，我们可以参照该班上一次考试的数据进行比较分析。

假设仍是上述三班，他们前一次数学考试的标准差（参照上面介绍的方法进行计算）分别为：A班10分；B班-7．8分；C班-11．9分，见表2。

表2　某年级三个班两次考试标准差

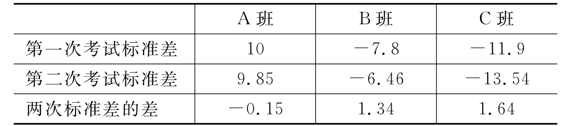
比较可以发现：A班标准差变小，由于两次考试标准差都为正，所以标准差变小意味着成绩退步了。B班和C班两次考试标准差都为负，但第二次考试标准差绝对值都变小，说明他们的成绩更靠近年级平均成绩了，因此他们在进步，并且C班进步的幅度更大。

综合比较，可以得出结论：第二次考试C班教学质量最好，因为经过教学，学生进步了，且进步较大；A班教学质量最差，因为经过教学，学生成绩下滑了。

将这种评价方法应用到实际的教学系统中，不论如何进行分层教学，也不论班额数多少，都可以方便地进行比较，因为它不仅进行了横向比较（计算本次考试的标准差时取全部学生数据作参照，就体现了这种思想），也进行了纵向比较（比较本次考试与上次考试的标准差，确认教学以后的学生状态），因而是一种比简单地比较平均分更为科学合理的教学质量评价方法。

当然，实际操作中，也不可能完全绝对地简单比较两次考试标准差，因为，比如在当前的分层教学中，火箭班（就是成绩较好的班级，各地叫法不一样）的标准差不仅肯定为正数，而且肯定还较大，如果要求教学后，一次比一次只能进步，不能后退，这显然不合理；而那些基础较差的班级，虽然他们取得了进步，但并不表示老师付出的一定比那些基础好但考试成绩退步的老师付出要多。比较可行的办法是，既比较标准差的变化，又允许标准差在一定范围内变化。

二、基于马尔柯夫链的评价方法(www.xing528.com)

（一）马尔柯夫链评价的数学模型

在一个随机过程中，如果由一种状态转移到另一种状态的转移概率只与现在处于什么状态有关，而与在这时刻之前所处的状态完全无关，这种过程就称为马尔柯夫过程。其中时间和状态都离散的马尔柯夫过程称为马尔柯夫链。

转移概率可以通过下面的实例来理解。假设每次考试无论学生成绩多么平衡或多么不平衡，我们总可以将学生按成绩分成上、中、下三等，经过一个学期的教学后，学生成绩的变化情况如下列矩阵所示：

其中，矩阵元素值表示的是各种情况的变化概率。如第一行第一列的元素值为0．7，表示原来是上等成绩，经过教学后，仍然保持为上等成绩的概率为70%，而第一行第三列的元素值为0．1，则表示原来为上等成绩，经教学后变为下等成绩的概率为10%，其他依此类推。这种矩阵称一步转移矩阵，它是最基本的。

如果上述一步转移矩阵所表示的概率是稳定的（称为平稳转移概率），并且各种教学条件稳定（如教师的教学态度和教学方法不变、学生的学习态度和学习能力不变等），那么我们就可以预测经过若干学期教学后，学生最终可能到达的状态，并以此作为评价教师教学质量的依据。

如假设某班有30人，按成绩分类，上、中、下等各有10人，则初始状态的成绩矩阵为：X（0）＝（10/30，10/30，10/30），按p（1）给出的转移概率，可以预测经过一个学期教学后的成绩矩阵将是：X（1）＝X（0）·P（1）＝（10/30，10/30，10/30）

这表示，经过教学后，上等成绩的学生数减少了1人，下等成绩的学生数也减少了1人，而中等成绩的学生数则增加了2人。

同理，可以预测经过两学期教学后的成绩矩阵将是：X（2）＝X（1）·P（1）＝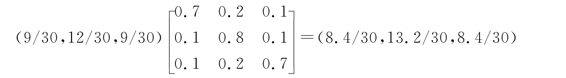

这表明，经过两个学期教学，上等成绩和下等成绩的人数都在按一定规律减少，而中等成绩人数则按一定规律增加。

（二）马尔柯夫链在教学评价应用中的实例分析

某校初三开始，分别由A老师和B老师接替原来的老师，承担初三（1）班和初三（2）班的英语教学，下面列出两班初二期末考试和初三第一次考试的成绩。表3是初三（1）班考试成绩，表4是初三（2）班考试成绩。其中S1表示初二期末考试成绩，S2表示初三第一次考试成绩。

表3　初三（1）班英语考试成绩转移情况表

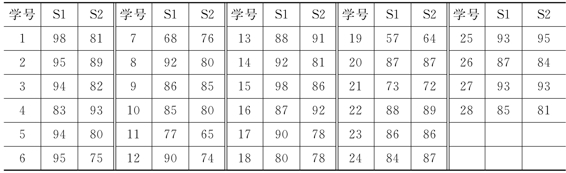
表4　初三（2）班英语考试成绩转移情况表

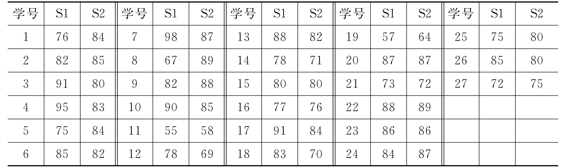
计算得，初三（1）班平均成绩为82．29，初三（2）班平均成绩为79．89，但初二期末考试两班平均成绩分别为86．61和80．67。因此，不能简单地认定（1）班教师的教学质量一定比（2）班教师教学质量高。

下面简单介绍用马尔柯夫链分析法对上述数据进行处理的过程。

步骤1：将学生成绩分成5类，并统计初二期末英语考试中每班各类学生的人数。需要说明的是，分成多少类并不是固定不变的，也可以根据本校上一届学生的考试情况或上级教育机构下达的指标进行分类，如上一届学生10人考上重点，30人考上普通高中，其他考上各类职业学校，则类别数就是3，并据此统计各班有多少人进了全校前10名，有多少人在全校排名为第20～40名之间等。由此得到向量X（A）和X（B），其中X（A）表示（1）班的成绩矩阵，X（B）表示（2）班的成绩矩阵，矩阵元素值中的分母表示班级总人数，分子表示属于相应等级的学生数。

X（B）＝（6/27，9/27，9/27，2/27，1/27）

步骤2：考察初三第一次考试成绩，获得转移矩阵P（1）和P（2）。

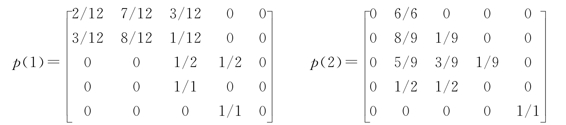
其中，每一行的分母表示初二期末考试属于相应类别的人数。如P（1）第一行的分母12表示初二期末考试有12人成绩属于第一类，P（1）第二行的分母12表示初二期末有12人成绩属于第二类，P（1）第三行分母2表示初二期末有2人成绩属于第三类，等等。而每一行的分子意义则比较复杂。如P（1）第一行第一列元素值为2/12，其分子2表示上次考试成绩属于第一类而本次考试成绩也属于第一类的人数为2人，P（1）第二行第三列的元素值为1/12，其分子1表示上次考试成绩属于第二类的学生中，本次考试成绩属于第三类的人数为1人。

步骤3：对初始矩阵和转移矩阵进行数学处理（求特征值和特征向量），得到极限状态向量为：

X′（A）＝（0，0，0．667，0．333，0）

X′（B）＝（0，0．801，0．146，0．016，0．037）

步骤4：结果解释。

极限状态向量说明，在教学质量、教学条件稳定的情况下，学生总体上可能达到的程度（与学生的基础无关）。由X′（A）和X′（B）可知，（1）班有66．7%的学生可能达到70～79分，33．3%的学生可能达到60～69分。（2）班有80．1%的学生可能达到80～89分，14．6%的学生可能达到70～79分，两项相加接近95%，因此，（2）班教师教学质量更好。

三、小结

以上介绍的两种教学质量评价方法中，基于标准差的评价直接以前一次考试情况为基础，比较本次考试相对于前一次考试是进步还是退步，因而相对平均分的评价方法而言，能更全面客观地反映教师教学对学生的影响；基于马尔柯夫链的教学评价，虽然也参考了前一次考试的结果，但它更体现教师教学对学生未来成绩的影响，因而是从预测的角度进行教学评价的。毫无疑问，两种方法尽管侧重点不同，但都不失为科学合理的教学质量评价方法。

必须提到一点，以上两种方法都须借助于一定的数据处理技术，在计算机技术高度发达的今天，这实际上已经不成为问题。相信这些方法对推动中小学教师教学质量评价有所帮助。

参考文献

［1］薛理银．教育信息处理原理［M］．北京：北京师范大学出版社，1996．

［2］傅德荣．教育信息处理［M］．北京：高等教育出版社，2002．

（作者单位：江汉大学教育学院媒体技术系）