中国城市土地价格微观决定机理研究成果

3.2.1　单中心城市模型下地价形成的理论分析

单中心城市模型产生于20世纪70年代左右，Alonso^［10］、Muth^［11］和Mills^{［12—13］}为其建立做出了突破性的贡献，因此，文献中通常也将单中心城市模型简称为AMM模型。之后，Brueckner^［137］对AMM模型进行了发展和完善^[1]，使得单中心城市模型在解释城市空间结构及其演变方面一直占据主导地位。正如Arnott^［138］所评述的，单中心城市模型奠定了新城市经济学（New Urban Economics）的基石，使城市经济学理论的研究完成了由局部均衡向一般均衡发展的重大转变。

单中心城市模型描述了一个简单的静态城市空间结构：假定就业活动集中在城市中心地区（CBD），家庭会权衡不同区位的通勤成本和房价水平从而进行选址决策。在单中心城市模型下，城市空间结构强调的是家庭的区位选择。

单中心城市模型中假设城市是一个均质、平坦的圆形区域，城市所有的就业活动集中在CBD，将其看做是一个点；城市中有N个居民，每天需要通勤到CBD工作，其工资水平为y；居民的通勤成本与其居住地到CBD的距离成正比，假定单位往返距离的通勤成本为t（只考虑货币成本，不考虑通勤的时间成本）。居民以效用最大化为目标，其效用方程为u（q，c），其中，q为住房服务的消费量，c为住房以外的其他商品的消费量。假定到CBD的距离为x处的住房租金为p（x），而其他商品的价格不随空间发生变化，将其设为1，则居民的预算约束条件为

居民会选择最优的消费组合（q，c），以实现效用的最大化，即

作为住房建设者的开发企业，其住房生产函数为H（L，K），其中，L为土地的投入，K为资本的投入。假定土地的租金水平为r（x），资金成本即利息率为i，则开发企业的利润函数为

在完全竞争的市场条件下，π＝0，由此可得

假设住房生产函数为一阶齐次函数（Homogenous Function of Degree One），则

式（3.5）中，S代表资本密度，即S＝K/L；h（S）代表地块的开发密度，即h（S）≡H（S，1）；并且由一次齐次条件可得h′（S）＞0，h″（S）＜0。

在空间均衡的条件下，居民的最优效用在不同区位是无差异的。对式（3.1）和式（3.2）的优化求解问题可以简化为

(www.xing528.com)

将式（3.6）对q求极值，可以得到居民效用最大化的必要条件为

式（3.7）中，u₁代表效用函数u（q，c）对第一项的偏微分，u₂则代表效用函数u（q，c）对第二项的偏微分；式（3.7）揭示了不同预算约束条件下的最优住房消费量的选择。

将式（3.6）对x进行全微分，可得

式（3.8）表明住房价格（租金）随着到CBD距离的增加而减小。在满足最优效用空间不变的条件下，住房价格与住房服务消费量之间存在替代效应，如图3-2所示。

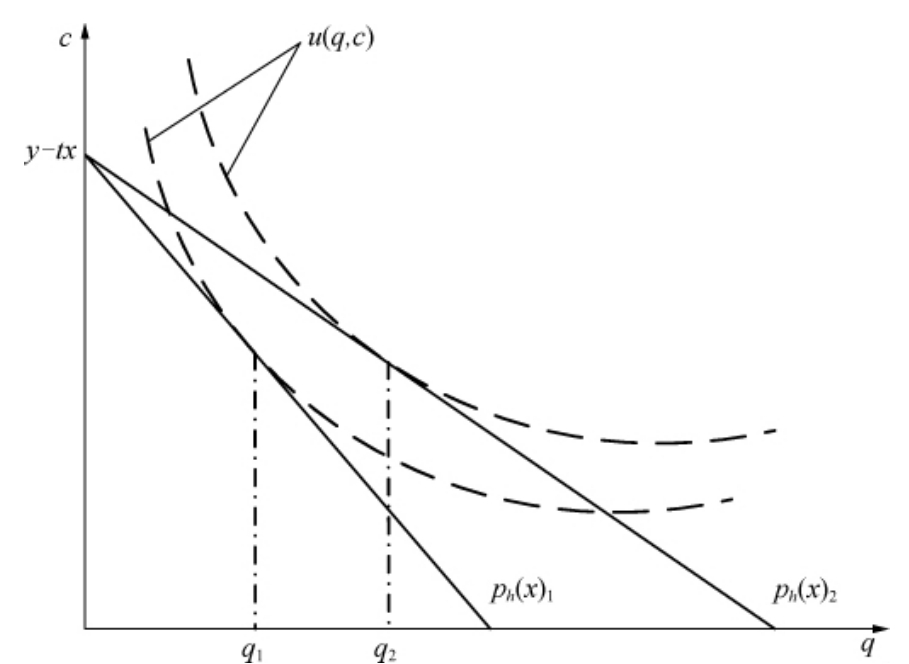
图3-2　住房价格与住房消费量之间的替代效应

为进一步推导地价在空间上的变化规律，需要对开发企业的利润最大化函数进行微分运算。将式（3.3）对S求导，得

将式（3.5）对x进行全微分，并代入式（3.8）和式（3.9）的计算结果，可以得出

式（3.10）的结果揭示了城市土地价格（租金）的空间分布规律：地价随着到CBD距离的增加而减小。这是单中心城市模型的一个重要推论。在利用该推论进行实证研究时，文献中通常将地价与到CBD的距离之间设定为指数函数的形式，即

式（3.11）中，α通常用来表征价格梯度，f（g）代表除到CBD的距离以外的其他影响因素与地价之间的函数关系。