B-P神经网络算法在我国石油企业可持续发展力评价研究中的应用

7.3.2　B-P神经网络算法

B-P神经网络算法由数据流的正向传播（前向计算）和误差信号的反向传播两个过程构成。由于每层神经元的状态只影响下一层神经元，所以正向传播时，传播方向为输入层→隐含层→输出层。如果输出层得到的不是期望输出，那么误差信号就会反向传播给输入层。一方面通过数据流的正向传播过程和误差信号的反向传播过程的不断交替进行，另一方面在权值上通过动态迭代搜索一组权向量，并执行误差函数梯度下降策略，这样做是使网络误差达到最小值，经过大量样本的训练与重复的调整后就完成信息提取和记忆过程。

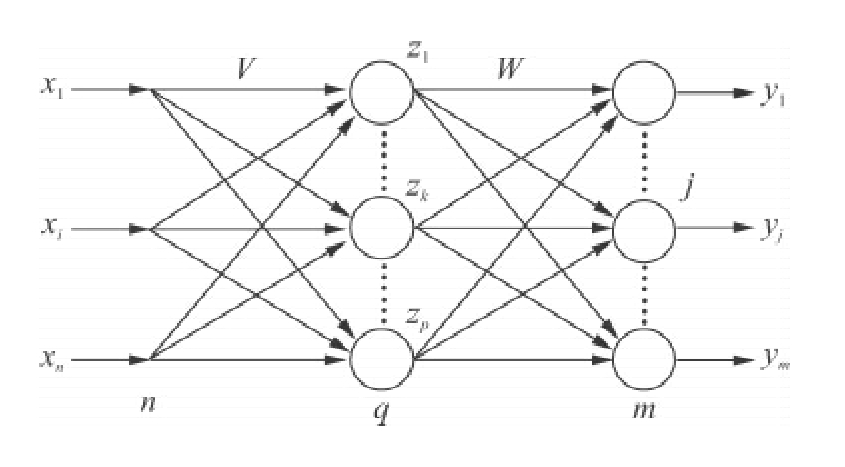
图7-4　B-P三层神经网络的拓扑结构图

（1）数据流正向传播

如图7-4所示在最左边，B-P神经网络的输入有n层；图的中间，隐含层有q层；图的最右边，输出层有m层，输入层与隐含层之间的权值为v_ki，隐含层与输出层之间的权值为w_jk，如图7-3所示。如果隐含层的传递函数为f₁（·），输出层的传递函数为f₂（·），将阈值代入求和项中即得隐含层节点的输出：

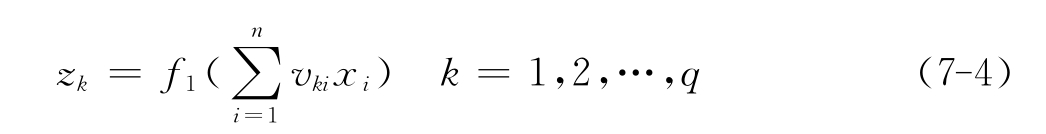
输出层节点的输出表示如下：

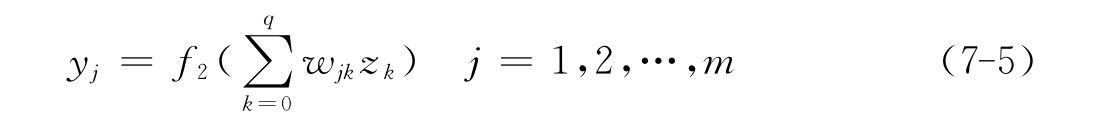
到这里B-P网络就完成了数据流从n维空间对m维空间的近似映射。

（2）误差信号反向传播

1）误差函数的定义

在这里用x¹，x²，…，x^p来表示p个学习样本。当第p个样本输入到网络中，可以得到实际输出y^p_j（j＝1，2，…，m）。因为采用平方型误差函数，所以Ep表示第p个样本的误差（t p_j为期望输出）：

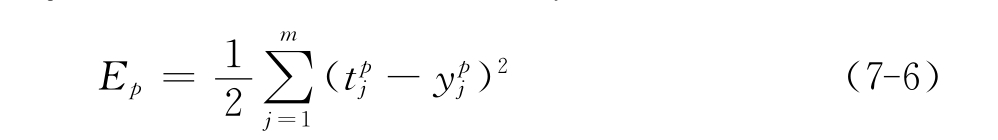
那么所有p个样本的全局误差为：

2）隐含层权值的变化

首先定义误差信号为：

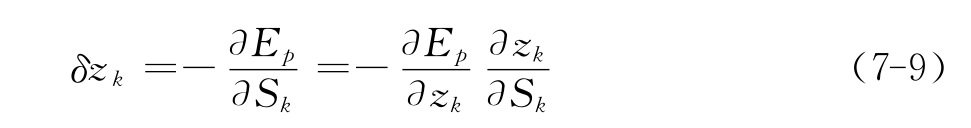
其中第一项为：

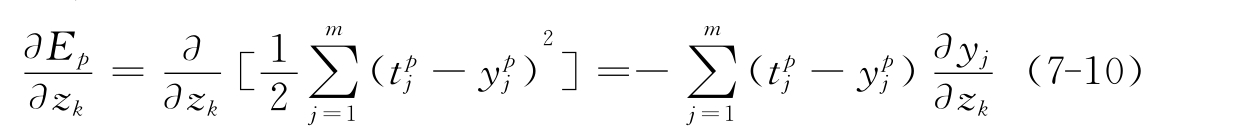
由链定理得：

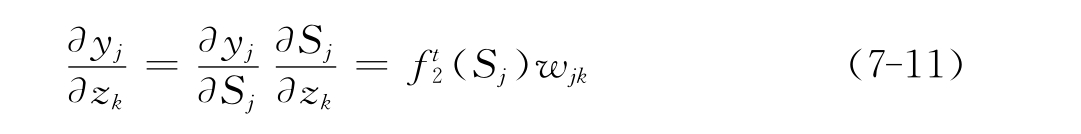
其中第二项为：

(www.xing528.com)

是隐含层传递函数的偏微分。于是：

由链定

于是得到隐含层各神经元的权值调整公式：

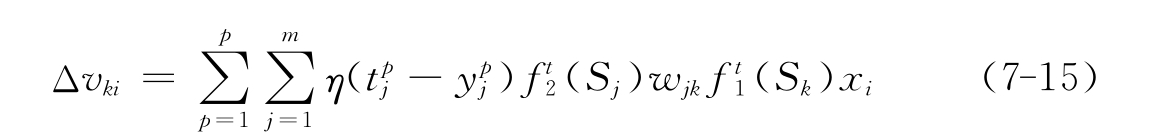
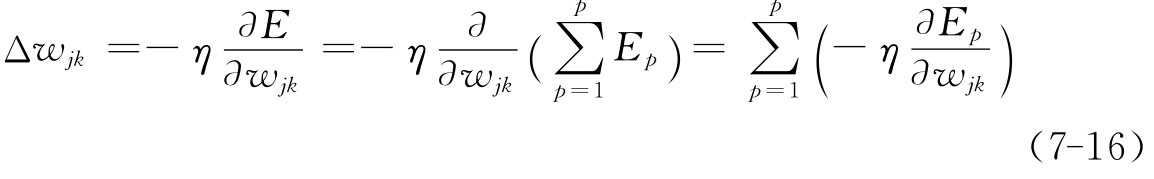
3）输出层权值的变化

如采用误差函数梯度下降策略B-P神经网络算法调整wjk，就可以使全局误差E变小，即（为学习率）：

定义误差信号为：

式（7-17）中第一项为：

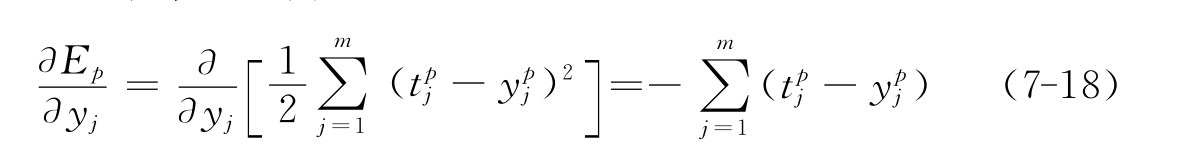
第二项：

为输出层传递函数的偏微分。

于是：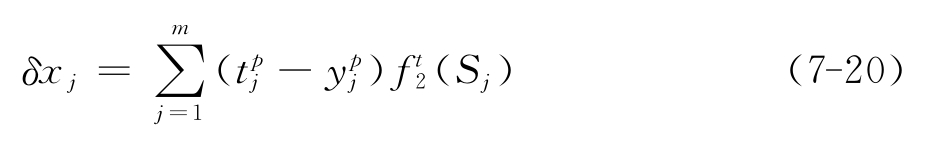

由链定理可得：

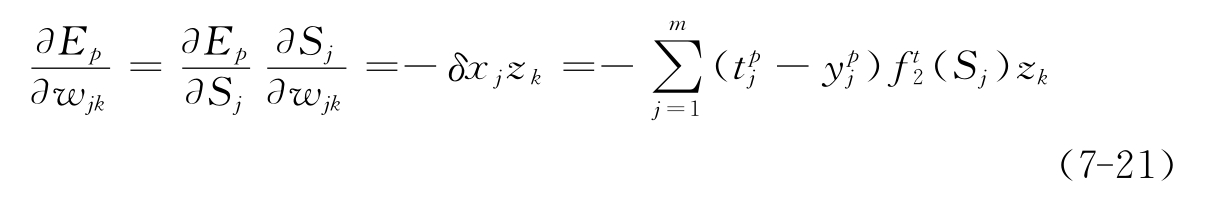
输出层各神经元的权值调整公式为：

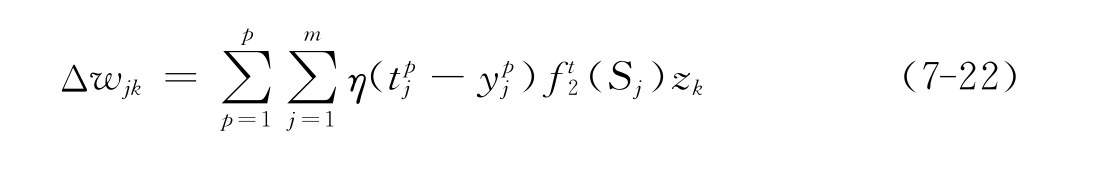
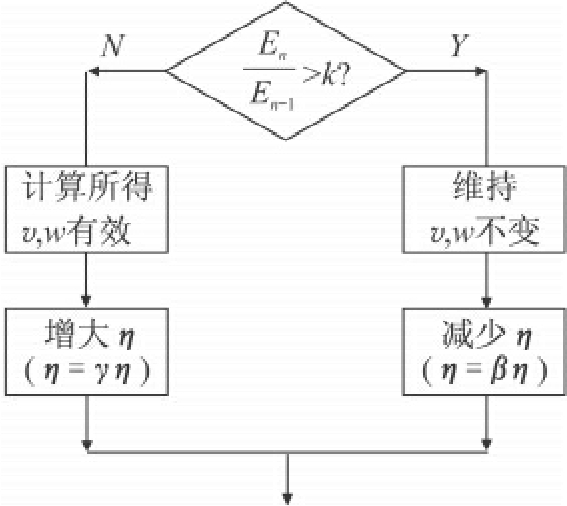
图7-5　自适应调整学习速率