教师领导力研究：提炼升华引领成长

教师专业发展已由少数个体的自觉主动行为发展到行政引导、专家指导下的群体发展状态，现在，教师专业发展的特点是行政推动、专家引导、群体发展、自觉性高。近几年，我结合自己的专业发展历程和周围一些优秀教师的成长案例（如华南师大附中的李兴怀、罗碎海老师、省级教师工作室主持人、市级名师工作室主持人），对教师专业发展做了系列研究，深化了对教师专业发展的认识。

在深入研究的基础上，2010年，在东莞市高一数学教师培训会上作了《青年教师的专业发展》讲座，2011年和2012年，两次受邀在英德市骨干教师培训班上作了两期讲座——《教育智慧与教师专业发展》，2011年受邀在河北省香河一中、东莞一中等多所学校作了《教师专业发展的路径与目标》等报告，这些报告对教师专业发展的内容、途径、目标及动力作了全面分析，当时，邀请方要求我以自身发展的经历并结合省内杰出教师的成长案例进行讲解，案例生动，讲座得到好评。

2012年受邀到河北香河一中进行了为期一周的驻校指导工作，对该校数学教学进行了全面剖析、指导。

我及工作室同仁对备课、上课、课后反馈等作了一定研究，使日常琐碎的工作科学化、规范化，并力求精细化，力争做到高效、优质。例如，学生作业及练习的选编与创拟，这是一个在教学中经常遇到的问题。由于数学本身就是一个题海，不能因为是题海就采取题海战术，让学生做大量作业或进行高强度练习；正确的方法是教师入海，要精挑细选题目；因此，怎样选编一些有训练价值的题目作为作业或练习，就成为日常教学工作的有机组成部分，我们就此作了一些研究，形成了选编练习题的准则与机制。

案例6：专题讲座《命制高中数学周练试卷漫谈》

东莞市第一中学　孟胜奇

一、试卷功能分析

不同类别的数学试卷有不同的功能，在命制试卷前，首先要弄清楚本次测试对试卷提出的功能性要求。

1．高考试卷的功能：①选拔功能；②教育导向功能。

2．统考试卷的功能：①考查功能（终结形成性考查）；②水平测试功能。

3．月考试卷的功能：①阶段形成性考查功能；②水平测试功能。

4．周测试卷的功能：①数学训练功能；②检测与反馈功能；③水平测试功能。

二、周练试卷的命制

根据周测数学试卷的三个主要功能，进一步明确本周训练与检测的知识要点和主要数学方法，明确技能要求、难度分布和题型布局，列出知识清单，在选择（或编拟）数学试题时，首先根据知识重点，选编解答题（大题），再利用客观题（小题，即选择、填空题）来补充。命制一套周测试卷一般要经过准备与布局、选（编）题与组卷、检查与修订等几个环节。

1．准备与布局。①确定试题（卷）难度：由于周测试卷的主要功能是训练与检测，对教学效果提供必要的反馈信息，因而试题的难度应在0．4至0．9之间分布，整卷难度控制在0．63至0．73，即95分至110分之间。②确定知识点分布：根据课标与考纲要求，按掌握、理解、了解等不同层次要求，对涉及到的板块的基本知识与基本技能进行筛选，清理出重点知识点和一般知识点，再布点编选试题。③确定数学方法与数学思想：数学方法与数学思想也是重要知识点，对此也要进行必要的梳理，融入试题，进行训练与考查。④确定题型：数学题型有判断题、证明题、计算题、求解题、探索题（存在性问题、开放性问题），根据所学内容以及题型发展趋势，设置恰当题型。⑤确定补漏知识点：根据作业和前次周测的反馈信息，对于一些必须掌握和熟练应用而没有达到要求的知识点（基本知识、基本技能、数学方法、题型），设置变式题进一步训练。⑥掌握试题发展趋势：通过研究广东、山东、海南以及京、津等地近年高考试题及模拟试题，掌握命题的核心思想和试题的发展趋势。

2．选（编）题与组卷。①筛选：阅读教材、教辅资料、有关测试卷，从中筛选符合考查目的且有训练价值的题目。②改编：对筛选出的题目，部分可以直接使用，有的则根据考查知识点、难度等要求适当改编。③组卷：将题目按选择题、填空题、解答题等不同题型从易到难依次编排，组成一套完整试卷。

3．检查与修订。一般提前2至3天命好题，利用这段时间进行反思，发现问题。①检查分值分布：全卷150分。将选择题均分控制在42分左右，填空题均分控制在15分左右、解答题均分控制在48分左右；解答题第一题应是送分题，第二题难度略有提高，控制在10分左右，即使最后一题，也应让多数学生能够动手答题，均分控制在4分左右。②检查知识覆盖：对要考查或训练的知识点、技能、数学方法进行检查，看是否均已覆盖。③检查文字与符号：通读全卷，对文字的规范性和表述的准确性等方面仔细斟酌，数学符号是否正确。④修订：依据课标、考纲要求和训练目标，对存在问题进行修订，以使整卷达到命题要求。

高一、高二新授课知识点不多，前半学期一般1套题可覆盖所学内容，到后半学期两套题可覆盖所学知识；周测采用知识滚动方式命题，以减少学生遗忘；高三力争3套题覆盖全部知识和主要题型。

三、试题的编制

试题的编制手段有选、改、编、创。由于周测的常态化和命题时间限制，周测试题一般选用成题，但根据考查内容的需要，对有些成题进行一定的改编甚至创作新题都是必要的，下面谈谈编制试题的具体方法与案例：

1．选题：选题来源于各地形成性测试题、终结性测试题、模拟题、高考题，所选题要符合考查内容、难度要求，尽量避免熟题和艰涩问题；有的题目虽然是高考题，但缺乏生命力，没有训练价值。

案例1　2009年江西省高考题。不足：入口太窄，技巧性过强，没有使用价值，缺乏生命力。

各项均为正数的数列｛an｝，a1＝a，a2＝b，且对满足m＋n＝p＋q的正整数m，n，p，q都有

（1）当时，求通项an；

（2）证明：对任意a，存在与a有关的常数λ，使得对于每个正整数n，都有。

2．改编：改编题同样来源于各地段考、终考、模拟、高考试题，也可选自课本的例题或习题；改编的方式可以是对条件的添、减、变，也可对背景进行更换，还可对设问方式以及思路进行转换。

案例2　2010—2011学年度第一学期高三统考理科试题的改编。

为了调查老年人的身体状况，某老年活动中心对80位男性老年人和100位女性老年人在一次慢跑后的心率水平作了记录，记录结果如下列两个表格所示，

表1　80位男性老年人的心率水平的频数分布表（单位：次／分钟）

表2　100位女性老年人的心率水平的频数分布表（单位：次／分钟）

（1）从100位女性老人中任抽取两位作进一步的检查，求抽到的两位老人心率水平都在［100，110）内的概率；

改编为：（1）按分层抽样的办法从80位男性老人中抽取8位老人，问从心率水平为［90，110）的老人中抽取了几人？接着，在抽取的这几位老人中选两人进行视力检查，问进行视力检查的两位老人的心率水平均属于［90，100）的概率？

3．编创：编创以创为主，改编为辅的制题方式，对原题进行了较大的改动，考查的知识点和数学方法与思想有了显著变化。

案例3　人教社选修1—1P43—B组第一题的改编。融合了导数等知识；知识点由单纯的求轨迹问题变为涉及直线、椭圆、抛物线、导数和分类讨论思想的综合题，入手容易，整体难度不大。

已知椭圆方程为），抛物线方程为x2＝4by。过抛物线的焦点作y轴的垂线，与抛物线在第一象限的交点为A，抛物线在点A的切线经过椭圆的右焦点F。

（1）求满足条件的椭圆方程和抛物线方程；

（2）设P为椭圆上的动点，由P向x轴作垂线段PQ，垂足为Q，且线段PQ上一点M满足｜PQ｜＝λ｜MQ｜，求点M的轨迹方程，并说明轨迹是什么曲线？

解：（1）抛物线的焦点为（0，b），过抛物线的焦点垂直于y轴的直线为y＝b。

由得点A的坐标为（2b，b）。由x2＝4by易得x，故。

∴抛物线在点A的切线方程为x－y－b＝0。令y＝0得x＝b，∴F的坐标为（b，0）；

又由椭圆方程知F的坐标为）。∴，解得b ＝2。

∴椭圆方程为，抛物线方程为x2＝8y。

（2）设点P的坐标为（x0，y0），点M的坐标为（x，y），则点Q的坐标为（x，0），且x0＝x，y0＝λy。将其代入椭圆方程得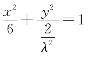（λ＞0）。

当时，M的轨迹方程为x2＋y2＝6，轨迹是圆；当时，点M的轨迹方程为，其轨迹为椭圆。

案例4　变换条件或添加设问设。

（1）将f（x）化为Acos（ωx＋φ）＋b（A＞0）的形式，并求出f（x）的最小正周期及单调递增区间；(www.xing528.com)

（2）若锐角α满足f（α）　√＝3－2　3，求tanα的值；（3）将函数f（x）的图象向右平移π3个单位，横坐标再伸长到原来的2倍，得到函数y＝g（x）的图象。求函数F（x）＝在x处的切线方程。

解：（1）

∴f（x）的最小正周期为T＝π，单调递增区间为，kπ－。

（2）由得。

∵0＜α＜，∴＜2α＋＜π，∴2α＋＝π，即α＝。。

（3）依题意，，∴

。，切点为。∴切线方程为即4x＋π2　y－4π＝0。

案例5　递进增加思维量，考查要害。

求三视图的侧视图的面积。根据学生年龄的增长、理解能力的增强，设置的几何图形不断演化，但紧紧抓住了三视图的本质。

4．创作：创编题可借鉴已有题型采用类比的方法创作；也可直接构造新情景，构思新立意；还可从生产实际中归纳、提炼、构造数学问题；更多的是从日常探究过程中发现编拟问题。

案例6　置换问题背景

文科的概率问题主要是古典概型和几何概型，两种概型的特点都是每个结果的发生具有等可能性，只是古典概型的所有可能出现的基本事件只有有限个，而几何概型每个事件发生的概率只与构成该事件的区域长度（面积、体积）成比例，所有可能出现的基本事件有无限个。抓住这一本质特征，可变换问题背景，得到一系列新题。

（1）一元二次方程的根。

海南、宁夏2007年文科第20题：设有关于x的一元二次方程x2＋2ax＋b2＝0。

（Ⅰ）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率。

（Ⅱ）若a是从区间［0，3］任取的一个数，b是从区间［0，2］任取的一个数，求上述方程有实根的概率。

（2）置于线性规划背景中

已知约束条件（★）。

（Ⅰ）若x是从0，1，2，3，4五个数中任取的一个数，y是从0，1，2，3三个数中任取的一个数，求点（x，y）落在区域（★）外的概率；

（Ⅱ）若x是从区间［0，4］任取的一个数，y是从区间［0，3］任取的一个数，求点（x，y）落在区域（★）内的概率。

（3）置于函数背景中

已知函数f（x）＝。

（Ⅰ）若a是从0，1，2，3，4五个数中任取的一个数，b是从0，1，2，3三个数中任取的一个数，求函数f（x）有极值的概率；

（Ⅱ）若a是从区间［0，4］任取的一个数，b是从区间［0，3］任取的一个数，求函数f（x）在（－∞，＋∞）上单调递增的概率。

（4）置于立体几何背景中

可在空间坐标系中构造一个与长方体内的格点有关的古典概型和与体积有关的几何概型问题，这里需要设置三个变量，题例从略。

案例7　已知函数在R上是增函数，求实数a的取值范围。

创作：数列｛an｝单调递增数列，且（0＜t≠1，n∈N＊），求参数t的取值范围。　【答案：】

案例8　2009——2010学年度第二学期高二期末统考试题

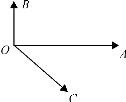
如图，已知∠AOB＝90°，∠AOC＝45°，且，。

（1）试用向量来表示向量；

（2）若向量的终点在一条直线上，求实数k的值；

（3）设（t∈R），t为何值时，A、B、C、D四点共圆。

解：（1）以直线OA为x轴，OB为y轴，如图建立直角坐标系。

则＝（1，－1）。

所以2。（2）令），则＝（k－2，－k）．　（6分）由题意知，所以－2×（－k）－（k－2）＝0，解得k＝－2。

（3）设过点A、B、C的圆的方程为x2＋y2＋Dx＋Ey＋F＝0。

易得

所以D＝－，E＝－，F＝－。

所以圆的方程为x2＋y2－x－y－＝0。

又。因点D在过点A、B、C的圆上，

故0，即3t2－t－4＝0。解得t＝－1，或t＝。

所以t＝－1，或t＝时，A、B、C、D四点共圆。