高中数学课型研究成果

数学教育的意义远远不只是知识的传授，更为重要的应该是对青少年的心智、潜能的开发与提升，是深刻的、长远的，而且也是其它学科所不能替代的。［3］数学教育的核心是教育，是以数学为载体的教育，其目的在于传承知识、培养能力和科学精神，这正是三维目标的体现。作为教育的组成部分，学生通过自主学习、探究活动，体验数学发现和创造的历程，理解基本的数学概念、数学结论的本质，在获得必要的数学基础知识和基本技能的同时，体会其中蕴涵的数学思想和方法，提高空间想像、抽象概括、推理论证、运算求解、数据处理等基本能力，提高运用数学提出、分析和解决问题（包括简单的实际问题）的能力，发展数学应用意识和创新意识，形成锲而不舍的钻研精神、理性精神和科学态度。

不同的数学课型，其学习内容和目标指向也不同，在教育功能和价值上存在差异，其教与学的方式也存在一定区别。例如，中学数学概念多是在对现实世界客观对象抽象概括基础上形成的，更多的用到归纳概括推理，而解题教学更多用到演绎推理，两类推理课的教学手段与组织形式也有显著差异；故而，基于促进学生发展这一目的，对于不同课型进行精细化研究，寻求与之适应且更有利于目标达成的教与学的方式就成为执教者的重要工作。

课型研究是教育发展到一定阶段的产物，是促进学生发展，追求教育价值的必然结果；课型研究是教育由粗放式到精细化转变的重要途径，是教师专业化的重要特征。

中学数学教育属于基础教育，功用在于为学生发展奠基的同时促进学生发展，涵义有三个方面：一是厚实学养，二是发展能力，三是形成品质。学生的发展必须体现在主体的能动性上，体现在学习活动中；课堂是学生发展的主阵地，课堂学习是学生发展的重要方式，教学内容是学生发展的主要载体。所以，将课按学习内容的特征划分或者按学习方式划分是最有利于学生发展的划分方式，是最常见的划分结果。

数学学习内容可以分为新授与巩固两类，新授内容可以分为：数学概念、数学命题、数学应用；巩固内容可以分为：数学练习、数学复习、数学测评反馈等。数学练习实质属于数学应用，目的在于提高数学应用的技能与熟练性，故而可以认为是同一类课——数学解题。因此，按学习内容的特征分类有：概念课、命题课、解题课、复习课、讲评课等。

课型的划分也可按教学方式划分，或者按学习方式划分。但教学方式与学习方式是辩证统一的，其价值取向具有一致性；教学方式影响着学生学习方式，学习方式的变化也促进教学方式的转变；一种教学方式的实施会产生与之相适应的学习方式。按“教”与“学”活动中学生参与的特点，教学方式可以分为讲授式、启发式、自学式、探究式、活动式、训练式等，对应地可以将课分为：讲授课、启发课、自学辅导课、探究课、活动课、训练课等。

这两种划分方法抓住了教与学的关键，一是教的内容，二是教的方式；这两种划分结果符合大多数教育者的认知，应能被广泛接受。在实践中，课型并不总是独立存在的，一节课，可能先学概念，接着学命题；也可能一部分内容采用讲授式，另一部分内容采用启发式，还有一部分内容采用探究式，因此，课型划分具有多样性与复杂性。本研究将在按学习内容划分的基础上，进一步探讨概念课、命题课、解题课、复习课、讲评课等课型的教学与学习方式，以便细致、深入地研究，实现数学教育的价值。

以上划分是对课的一级分类，在教学实践中，往往要更细致一些，如解题课中涉及数学应用问题的解决、解题技能训练问题等，就需要对有些课型进一步分类，这就是二级分类。如将解题课进一步分为应用课、技能课、数学思想方法课；命题课型中融入阅读课、探究课、研究性学习课（对应教材中的阅读、探究、研究性学习等栏目）；复习课中融入章末小结课；概念课前植入绪论课等。

其框架如下：

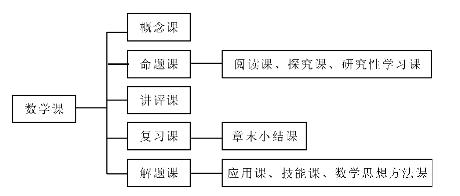
由于不同的课型，其教学目标指向与教育功能有所区别，教学方法有显著差异，为使课堂教学高质、高效，有必要对各类课型的教学进行分类研究。下面仅以概念课、原理课、讲评课为例。(www.xing528.com)

1．概念课

概念是数学知识的基本细胞，是数学内容的基本点和导出数学原理（定理、公式、性质、法则）的出发点。所以概念的学习是数学学习的核心，概念课的教学是教师落实基础的关键，是学生打好基础的首要环节，其教学价值在于培养学生辨析概括能力、实际问题数学化的能力、数学地分析问题的能力、创新意识与创新能力、表达能力等。概念课的基本教学流程为：①创设情境——教师展示概念的正例；②辨析讨论——教师引导或学生讨论，通过观察、思考，概括出正例的共同的本质属性；③形成概念——给出概念的定义；④概念辨析——学生举出核心概念的正例，教师举出核心概念的反例，深化对概念的认识；⑤概念应用——核心概念的应用等环节。

2．命题课

命题课是指有关中学数学核心命题的教学，是中学数学教学的重要课型。中学数学核心命题是指在数学概念形成之后，经过严谨推理证明或大量实践检验不证自明而得到的具有普遍意义的典型结论，如数学公理、定理、法则、公式等。数学核心命题具有高度的概括性与抽象性，在本质上描述了相关数学概念之间的关系。中学数学原理是中学数学的核心内容之一，是数学思维、推理、运算的基石。其教学程序为：提出问题—探究解决—生成命题—命题辨析—命题应用等。其中，对提出问题的探究解决是关键，其过程可以采用数学试验或者归纳、类比等合情推理手段，也可以用演绎推理方式。例如，在《直线与平面垂直的判定》的教学中，通过数学试验“过三角形ABC的顶点A翻折纸片，得到折痕AD，将翻折后的纸片放置在桌面上（BD、DC与桌面接触），观察怎样翻折才能使折痕AD与桌面垂直”（如图2），学生通过试验，容易发现“直线与平面垂直的判定定理”。这一过程，通过学生动手试验，在试验中发现定理，培养了学生的实践能力和创新意识。

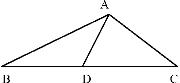
图2

数学命题蕴含着丰富的教育内涵，是培养学生推理能力、探究能力和创新意识、创新思维品质的重要素材，因而极具教育价值。因教材降低了难度等原因，对数学命题以不同的方式给出，在教学中，教师要区别对待。

3．讲评课

讲评课是对试卷的讲评，作用在于解惑与评介、提炼与拓展，许多教师只注意到“讲”、“评”，忽视了“提炼”与“拓展”，忽视对共性问题的深层次挖掘和思维层次的提升。讲评试卷课的程序是：考点归类—考情分析—错解评讲—要点总结—变式训练。备课时教师从考点分布、错解原因、典型思路、考情等方面进行试卷分析。错解评讲一方面对不会做或没做完的题目进行讲解，关键是寻找思路的突破口，打开思维通道；另一方面对典型错误、典型解法（好的方法）进行评析。要点总结有两个方面含义，一是对知识、方法要点进行小结，二是对重点知识、方法、数学结构进行提炼，通过延伸或进一步的探究对知识进行串联、深化。讲评课应在学生自主修正的基础上进行，关键是课前做好归类分析（如知识缺陷型、思维遇阻型、运算错误型等类别），讲评方式可以是师生互讲、互评。

数学概念、数学原理更多体现为创新，是培养提出问题的能力、探究解决能力、创新意识与创新能力的极好素材；数学习题、数学应用更多呈现为问题解决，是培养分析、解决问题能力的有效素材。这里简单的划分仅是侧重不同教学内容的主要教育价值，并没忽视其综合价值。