教师领导力研究成果：数学发展与教师实践

对中等数学的研究一直我教学研究的重心，涉及内容有一些新命题的发现，公式、定理、数学命题的推广，习题的别解，一些单元教学内容的专题研究等，这是我认为教好书的先决条件。因而我一边忙于日常教学，一边做做数学题，搞一点中等数学研究，边教书，边思考，边学习，边研究，厚实学科功底，夯实专业根基，丰富数学素养。工作三年后，我从1986年开始发表第一篇数学教学论文，此后几年，每年能够在中学数学教学研究类刊物上发表三至四篇论文，加上教学业绩也不错，逐渐在当地有了一些影响。

教学研究及成果对课堂教学的促进作用是隐性的，是个慢功夫，虽然自己感受到研究促进了自身专业能力的发展，提升了专业水平，但难以量化；不像有的行业，搞一些发明创造或技改，就能立即显现出其经济效益。

有一节课让我印象特别深刻，时至今日也难以忘怀！使我更加坚定了边教边研的信心，激发了进一步研究的兴趣。那是1987年秋开学后的第一节数学课，我走进课室，没带教材和教案，给学生讲的内容是当年一道立体几何高考题的多种解法及其推广和推广结论的应用，这是我当年暑假期间研究的一个结果。

该题是：如图1，在三棱锥P—ABC中，已知PA⊥BC，PA＝BC ＝L，PA，BC的公垂线ED＝h。求证：三棱锥P—ABC的体积V＝L2　h。

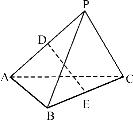
图1(www.xing528.com)

其推广是：设长为a，b的两条线段AB 和CD分别在两条异面直线l1，l2上滑动，两条异面直线所成角为θ，距离为d。则四面体ABCD的体积。

接着，我又用此结论解了三四道数学题，过程简洁、明了。

课后，学生评价很高，说从来没有听过这么精彩的课，没有一位老师以这种思维方式上过课，对自己是一次震撼和思维的洗练。由于是新学年第一节课，校长听到学生的反映后，找到我给予了很高的评价。这件事对我后来的教学产生了一定影响！回顾这节课的流程，是从个例出发，由特殊到一般，再谈一般性结论的应用，其思维的连贯性和逻辑的严谨性贯穿始终，一气呵成，探究味极浓，内容新颖。概括起来，这节课具有以下三个显著特点：（1）极强的思维性。该课从问题的相继提出，到逐个解决，环环相扣，步步深入，其严谨的思维贯穿始终，虽然教学方式依然是讲授式，但展现的数学思维的魅力深深熏陶着学生，使学生感受到思维的精彩；（2）富有成效的创新性。从高考题的一题多解，到命题的推广、推广命题的应用，随着教学进程的逐步展开、数学思维的深入，在探究过程中新的思维成果不断涌现，这些思维成果增添了教学的魅力；（3）可接受性。这节课的内容难易适当，符合学情，教学进程中每一步的探究都在最近发展区中，使学生理解到思维产生的价值。

想来，这应是该课成功的主要因素，更增添了我对中等数学研究及数学教学研究的兴趣，我后来提出的“研究式教学法”与这节课有很大关系。