企业信用评级模型研究：基于累积Logistic回归的实证研究

第四章　基于累积Logistic回归的上市公司信用评级模型研究

在探讨过信用风险量化模型的理论基础上，本章运用累积Logistic回归方法建立了一个企业信用评级模型的具体实例。公司信用评级的研究是从对公司财务困境的研究开始的，而其本质上是对违约风险测度的研究，即根据贷款企业的财务、非财务状况，利用统计学方法对企业的违约概率进行评估，然后按评级结果分为违约和正常两类，或者进一步细分为多类。国外关于信用评级的研究，主要集中于违约的定性测度方法，即根据计算结果，通过违约频率统计获得违约概率。测度方法根据变量选择的多少可分为单变量判别模型和多变量判别模型，根据违约测度方法可分为线性判别模型、Logistic回归模型和神经网络模型等。

关于企业违约风险的研究大都是基于以上的两分类法，并没有对违约风险等级做进一步的细分，也没有对企业处于每个风险等级的概率进行估计。在对企业违约概率的测度逐渐由序数违约概率向基数违约概率过渡的情况下，作为对公司违约率研究的拓展，将企业信用等级细化，并利用多元有序因变量Logistic风险测度模型估计企业处于各个信用等级的概率就很有必要。

第一节　公司违约风险测度的研究进展

公司违约风险测度的研究，从最初的单变量分析法，发展到以Z计分模型为代表的线性判别模型，以及到目前为止仍在使用的ZETA判别模型。在所有的多元判别模型中，Altman的Z计分模型是最优的（Scott，1981）。Altman利用ZETA模型研究了公司Z值与标准普尔、穆迪等评级公司公开发表的公司信用等级之间的关系，发现二者之间存在强烈的正相关关系（60%以上），因此可以利用Z值识别公司的信用等级。张玲（2004）利用Z值模型建立我国上市公司的信用评级模型。唐春阳、冯宗宪（2005）通过对29个财务指标采用逐步多元线性回归法，最后建立了一个7变量的企业信用违约率模型。

较早利用Logistic回归模型对违约率进行分析的文献包括Martin（1977）、Ohlson（1980）和Zavgren（1985）。其中以Ohlson的研究最具代表性，他采用1970～1976年105家破产公司和2058家正常公司为样本，建立了包括资本结构（总负债/总资产）等9个财务指标的违约率预测模型。由于只是两分类问题（违约和不违约），所以模型的预测率高达92%。Logistic回归模型作为线性判别模型的一种改进方法，国内相当多的学者也对它进行了研究，如陈晓和陈治鸿（2000）、吴世农等（2001）、马九杰等（2004）、于立勇等（2004）和梁琪（2005）等。

此外，神经网络作为人工智能的一种分类方法，也在违约风险评估领域中有所应用。如Altman等（1995）在意大利公司危机预测中使用了神经网络方法，Mdody Y.Kiang等（1992），Coats和Fant（1993）分别对美国公司和银行财务危机进行了预测并取得了一定的成效。但是Altman（1995）认为“神经网络分析方法在信用风险识别和预测的应用中，并没有实质性地优于线性判别模型”。

这些模型有着各自的特点和假设条件，学术界关于模型变量探寻的过程中，绝大多数是以财务变量为主，后来才陆续加入一些非财务变量，但是研究的核心仍然是以财务变量为主。这主要基于以下两个原因：①财务指标数据是通过容易取得的公开发表资料获取的，有较强的客观性，不容易引起争议；②过多地引入主观性和抽象性的变量，或采用不易获取并且无法证实的内部资料，都会大大降低模型的实际应用价值。所以，本书对于公司信用评级模型的构建，将全部采用可取得的公司财务指标。

线性判别模型的假定条件是极为严苛的，要求每组数据：①总体服从多元正态分布；②协方差矩阵相等；③均值向量、协方差矩阵、先验概率和误判代价是已知的。假定③可以通过样本数据对均值向量、协方差矩阵、先验概率进行估计得到解决。但是前两个假定对于很多样本数据是很难满足的。相比而言，Logistic模型不要求数据满足正态分布（其分布函数采用Logistic函数）。因此在数据不满足正态分布的情况下，采用Logistic模型能够提高模型预测的准确率。多元判别模型和Logistic回归模型这两种方法各有优劣，这取决于数据对各自假定条件的满足与否。但毫无疑问，由于Logistic回归模型对样本数据的要求较线性判别模型宽松，因而可以被看做是对线性判别模型的一种改进。

第二节　基于累积Logistic回归的上市公司信用评级模型

在设定二分类因变量Logistic模型的基础上，我们将建立多元有序因变量Logistic模型。由于我国上市公司信用数据具有高相关性和高维性的特点，因此在运用Logistic模型进行分析时，将不可避免地导致方程系数估计值的标准差增大，进而影响模型的稳定性和预测准确性。在进行回归的时候，虽然可以利用逐步选择法对指标进行筛选，但由于大部分原始数据信息的丢失同样会导致模型的预测准确性降低。因此，本书在进行多元有序因变量Logistic回归前，将利用因子分析法，找出能够将数据有效分离并能够保持原来变量大部分信息的主因子，以此达到降低维数和消除回归方程自变量的多重共线性问题的目的。

首先，利用公开的企业信用评级结果，在每个类别中选取若干样本，并从原来P个相关的原始变量中推算出K个公共因子，然后，以这K个主因子作为Logistic分析的解释变量来预测公司在每个信用等级的概率。为了便于比较，本书也将同时给出未经过因子分析的Logistic回归模型的估计结果。

一、指标选取

财务比率的设计和选取是度量企业信用风险的出发点，本书选取的财务比率大部分来自企业的财务报表。在参考了吴世农（2001）、范柏乃（2003）和梁琪（2005）等人的研究以及考虑了我国上市公司特色和研究需要的基础上，本书选择了能够反映公司盈利能力、经营状况、偿债能力、流动性、增长能力和管理水平的六大类共21个财务指标，建立综合评价体系，见表4－1。

表4－1　评价体系指标类型和基本指标

续表

企业信用等级标准采用国际通用的等级符号标记，分为AAA、AA、A到C 共7个等级。AAA信用等级最高，表示企业信用程度最高，长期偿债能力强，其信用风险损失的可能性最小；依此类推，C的等级最低，表示企业信用程度最弱，已经无法偿还其贷款，随时可能破产。在回归模型中，令AAA= 6，AA= 5，A= 4，BBB= 3，BB= 2，B= 1，C= 0。

二、数据处理——因子分析法

因子分析法作为主成分分析法的一个扩充，其本质思想在于：用几个潜在的但不能观察的随机向量去描述许多变量间的协方差关系，这几个潜在的随机向量就称为因子，利用此种方法可以在降低维数的同时并尽可能保持原有数据的信息。

因子模型用矩阵表示，即

其中，X＝（x1，x2，…，x）p表示p维的企业财务比率向量集，X是一个可以观测到的向量，其均值为μ＝（μ1，μ2，…，μ）p。F＝（f1，f2，…，fm）（m< p）表示m维的公因子向量集，L＝［Li］jp×m，Lij表示第i个财务比率在第j个公因子上的载荷，因此L也称为载荷矩阵。

本书利用主成分法进行因子分析。假定λj是原始数据阵X相关系数矩阵的特征值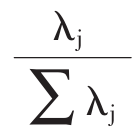，表示第j个主成分对总体数据的贡献率。对主成分按特征值大小进行排序，通常累积贡献率达到80%～90%时，确定公因子个数。本书选取85%作为分界点（cut poin）t。

利用式（4-1），可以通过它求得公因子fi的估计值，即

这里采用普通最小二乘过程生成公因子的估计值，公因子的估计值通常也称为因子得分。

三、模型设定

多元有序因变量Logistic回归模型定义为：

其中，y*表示观测现象的内在趋势，它并不能被直接测量，而ε为误差项。

当实际观测值有J种类别时（j＝1，2，…，J），相应取值为y＝1，y＝2，…，y＝J。并且各取值之间的关系为（y＝i）<（y＝j）（i< j，i，j= 1，2，…，J），那么共有J-1个未知阈值（threshold）或分界点（cut point）μj（j＝1，2，…，J）将各相邻类别分开，^[1]并且有μi<μj<（i< j）。

给定X值的累计概率可以由如下形式表示：

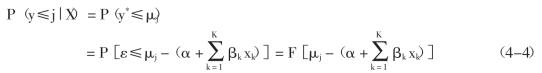
有了累计分布函数后，采用Logit作为对序次反应变量建模的关联函数。与对二分类因变量logistic回归类似，累计Logistic回归可定义为：

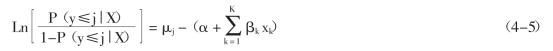
由（4-3）式，可以得到累计概率的预测公式：

一旦计算出累计概率，属于某一特定类别的概率如P（y= j），j=1，2，…，J，便可以计算出来。比如：

P（y= 1）= P（y≤1）

P（y= 2）= P（y≤2）- P（y≤1）

…

P（y= J）= 1- P（y≤J-1）

其中，

第三节　模型实证结果及分析(www.xing528.com)

一、样本选择范围及数据来源

基于上市公司财务指标及信息的完整性、客观性和可得性，本书选取沪深证券交易所88家上市公司为样本。各上市公司财务指标数据均来自WIND数据库；公司信用等级数据来自2005～2006年新华远东中国公开信用评级结果（PI）。

二、实证结果及分析

本书运用SAS8.2对经过标准化处理之后的财务比率进行了因子分析，共提取了8个公因子，累积方差贡献率达到86.09%。因子分析结果如表4－2所示：

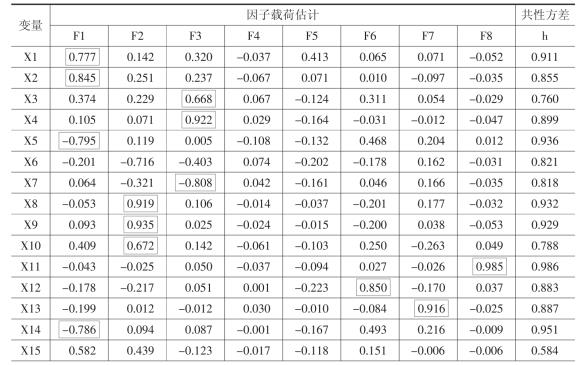
表4－2　因子分析结果^[2]

续表

从表4－2可以看出，X8-X10在F2上的载荷都超过了0.6，因此可以认为F2这个因子表示企业的还债能力；X16、X18、X19在F4上的载荷都超过了0.8，因此可以认为F4表示企业的增长能力；同样，X20、X21在F5上的载荷分别为0.907和0.889，因此可以认为F5表示企业的管理水平；而F6、F7和F8这三个因子均表示企业流动性；对F1和F3的解释则不是非常明晰。表示盈利能力的指标在F1上有较大的正载荷，而表示经营状况的指标在其上有较大的负指标，因此F1可以认为是表示相对于营业状况的盈利能力指标，不妨认为是相对盈利能力的度量。类似地，表示盈利能力和增长能力的指标在F3上有较大的正载荷，表示还债能力的指标在其上有较大的负指标，因此F3可以认为是表示企业相对于还债能力的发展能力，同样也可以认为是相对发展能力的度量。表4－3给出因子得分的结果。

表4－3　因子得分结果

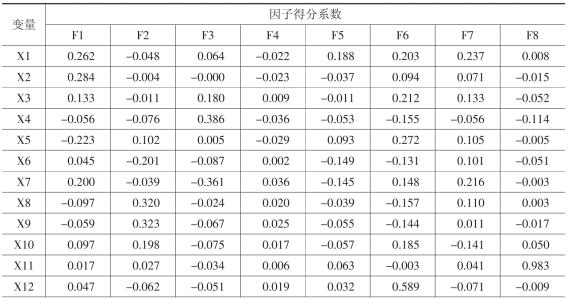
续表

利用表4－2可以得出各因子的估计值，然后利用估计出的F1~F8的值进一步做有序因变量Logistic回归。估计结果如表4－4所示。

表4－4　结合因子分析法的Logistic回归模型结果

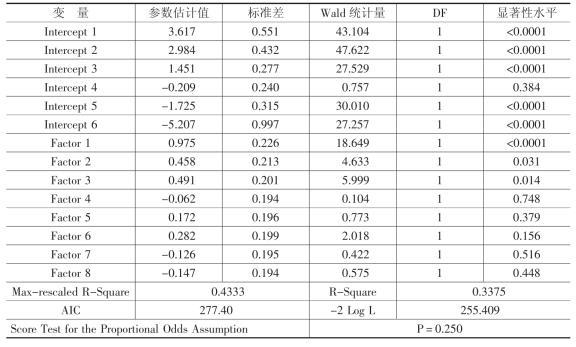
由表4－4可以发现主因子1，2，3，6对方程的能力较强，因此本书利用逐步选择法从8个主因子中选择出4个回归系数显著性在10%以下的变量，结果如表4－5所示。

表4－5　通过逐步选择法的Logistic回归模型结果

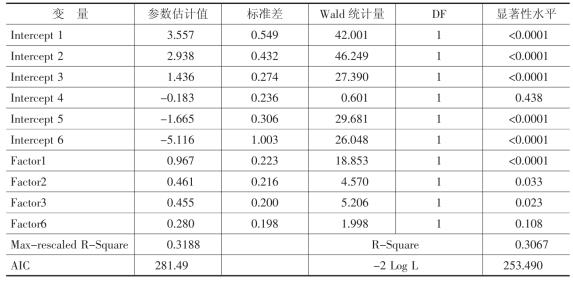
可以发现，模型参数的估计是十分稳健的，回归方程的拟合度较之前没有进行变量筛选的模型相比没有明显下降。

由表4－4和表4－5的结果，大致可以得出以下结论：

第一，通过逐步选择法的Logistic回归方程各回归系数均在至少10%的水平上显著，方程的AIC和-2LogL分别为281.5和253.5，不同于二元Logistic回归方程，这里是对六个信用等级估计各个信用的概率，因此方程的拟合度仅为0.4。

第二，对企业信用评级有正面影响的主要是企业的相对盈利能力、相对发展能力、还债能力和流动性，其中对信用评级影响最大的是企业的相对盈利能力，其次是相对发展能力和还债能力。

第三，企业绝对增长能力、管理水平和流动性对企业的信用评级没有显著影响，并且企业的流动性水平对企业的信用评级有负的影响。

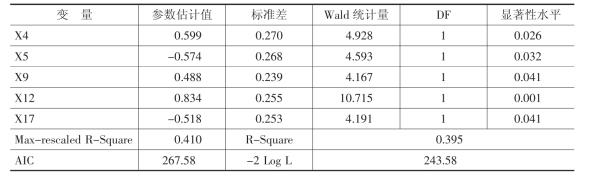
与此同时，本书也给出没有经过因子分析的多元序次因变量Logistic模型。结果如表4－6所示。

表4－6　未经过因子分析的Logistic回归结果

续表

三、实证模型预测准确度检验

基于以上分析和预测，得出经过因子分析的多元有序因变量Logistic回归模型的表达式，令其为模型1：

同样可得一般的多元有序因变量Logistic回归模型的表示式，为模型2：

利用新华远东2005年公布的信用评级结果，对模型1和模型2进行了准确度的检验，对最佳分界点，分别用50%、60%、70%进行检验，检验结果如下：

表4－7　模型1和模型2的准确度检验（N＝73）

可见，对最佳分界点的设定以60%左右为最优，模型1和模型2的预测准确度可以达到较好的水平。从总体来看，由于数据经过因子分析的预处理，模型1比模型2的预测准确度有了一定提高。但随着分界点的不同，预测的准确度没有非常显著的提高。这一方面是因为回归方程中样本数量较少导致极大似然估计效果不是很理想；另一方面是因为模型中没有考虑到其他环境因素导致模型设定上的偏差。

第四节　结论与模型的局限

本书探讨了利用Logistic模型进行公司信用等级的评价，既考查了历史数据，又分析了企业未来的发展前景，做到了信用评级的静态分析和动态分析相结合。考虑到公司财务指标的高相关性和高维性特点，本书通过因子分析法首先对原始变量进行了分析，然后利用估计得到的因子值进行多元有序因变量Logistic回归。从统计指标上来看，回归方程基本上能够对公司信用等级作出较为准确的评价。从预测结果上来看，经过因子分析的Logistic模型要优于一般的Logistic模型。虽然经过因子分析法的Logistic回归模型的预测结果没有比未经过主因子分析的Logistic结果显示出明显的优越性，但是，其回归方程中的自变量不存在共线性，因此所得到的结果也更令人信服。

本书的研究仅仅是通过上市公司的财务指标来对公司的信用等级进行评估，并没有考虑到行业因素和宏观环境对公司信用等级的影响。可以看到的Logistic模型的拟合优度仅仅为0.4，这一方面是因为本书不仅仅是二分类回归，而是对六个信用等级进行估计，拟合度下降是情理中的事；另一方面，由于本书中的样本仅仅只有80个，而进行Logistic回归所使用的极大似然估计法在小样本下的结果并不理想。因此，一方面可以通过分行业、分地区以及分规模来进行分类回归；另一方面可以通过扩大样本容量来提高模型回归的准确度。

从模型设定上来看，在进行等比例系数检验时可以发现：P值为0.25，处在显著与不显著的边缘。因此等比例模型是否能很好地拟合数据其实是有一定疑问的。对模型进行进一步的检验和改进也是今后研究的一个方向。

【注释】

[1]也即如果y*≤μ1，则y＝1；如果μ1<y*≤μ2，则y＝2；…；如果μj-1<y*≤μj，则y＝J。

[2]Xi（i= 1，2，…，21）与表4-1中的各基本指标相对应。