太平洋战争爆发后的中国与世界研究：CLOS网络

2．2．2　CLOS网络

交换网络的成本与网络的交叉点数密切相关，为了减少交叉点总数而同时具有严格的无阻塞特性，长期以来人们一直在寻求一种交叉点数（交换单元数）随输入、输出线数较慢增长的交换网络结构。克洛斯（CLOS）很早就提出了一种多级交换网络结构，并推导出了严格无阻塞的条件，这就是著名的CLOS网络。CLOS网络一般使用在大型电话交换系统中，属于多级交换网络。假设CLOS网络有M条入线和N条出线，如果M＝N，称该CLOS网络为对称的CLOS网络；否则为非对称的CLOS网络。非对称的CLOS网络目前很少用，因此下面以对称的CLOS网络为例，介绍CLOS网络。

1．三级CLOS网络的基本结构

一般来说CLOS网络是指三级CLOS网络，更多级的CLOS网络可以由三级CLOS网络构成。一个N×N的三级CLOS网络的基本结构如图2．24所示。

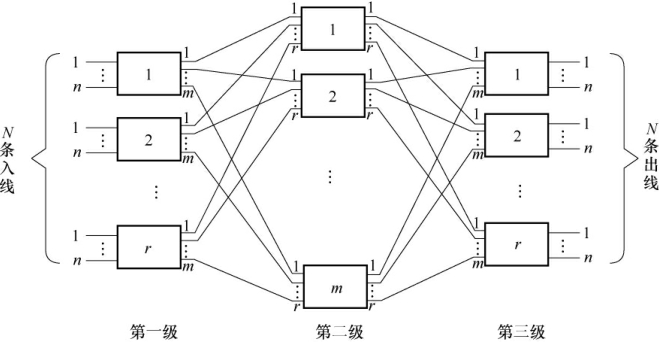
图2．24　三级CLOS交换网络

N为交换网络的入线、出线数。其中，入线N被划分为r组，每组有n条入线，即N＝r×n。第一级共有r个n×m交换单元，r组入线正好分别接入交换网络中第一级r个交换单元；假设第二级恰好有m个r×r交换单元，那么第一级的每一个交换单元就有m条输出，分别接到第二级中的m个交换单元；可以看出，第二级每一个交换单元共有r条输入线；第三级交换单元是m×n规模的，共有r个，第二级交换单元的r个输出分别连接到第三级的r个交换单元，这就是一个三级CLOS网络。它的两边分别有r个n×m和m×n的矩形交换单元，即N×N的三级CLOS网络是左右对称的，这就是“对称CLOS网络”的由来。对称CLOS网络的中间是m个r×r的方形交换单元。每一个交换单元都与下一级的各个交换单元有连接且仅有一条连接，因此任意一条入线与出线之间均存在一条通过中间级交换单元的路径。

2．三级CLOS网络无阻塞条件

（1）严格无阻塞的条件

三级CLOS网络有一个重要的特征，就是当满足某种条件时，不存在内部阻塞。下面分析推导三级CLOS网络严格无阻塞的条件。

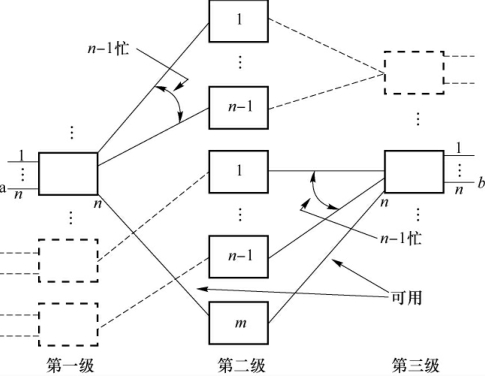
严格无阻塞的三级CLOS网络如图2．25所示，CLOS网络的第一级交换单元的入线数i ₁和最后一级交换单元的出线数o₃均为n，即i₁＝o₃＝n，中间级交换单元的个数n ₂＝m。如果要确立一条从a～b的信息交换通路，那么最不利的情况是第一级与a相连的交换单元中除去a之外所有剩余的n－1条入线均被占用，那么第一级与a相连的交换单元中，n－1条输出线均处于忙状态，并且所有的n－1条输出线都连接到中间级不同的交换单元上；最后一级与b相连的交换单元中，除b以外所有的n－1条输出线也均被占用，对中间级来说需要另外的n－1个交换单元，且这些交换单元都要有－条出线连接到与b相连的交换单元上。那么在最坏的情况下，需要中间级可选择的交换单元数为（n－1）＋（n－1）＝2（n－1）个，为了确保链路无阻塞，完成a～b的信息交换，至少还应存在－条空闲链路，即中间级交换单元数要有（n－1）＋（n－1）＋1＝2n－1个，因此得出三级CLOS网络严格无阻塞的条件为

也称为CLOS定理，其中，m为CLOS网络中间级所需要交换单元的个数；n为CLOS网络第一级交换单元的入线数和最后一级交换单元的出线数。三级CLOS网络只要满足以上条件就可确保严格无阻塞。

(www.xing528.com)

图2．25　严格无阻塞的三级CLOS网络

一般的CLOS网络严格无阻塞的条件为

（2）可重排无阻塞条件

对于三级CLOS网络，设i _l＝o₃＝n，n ₂＝m，当2n－1＞m≥n时，则称为是可重排无阻塞网络。也就是说，该网络虽然不是严格无阻塞的，但可以通过重新排序连接路径解决阻塞问题。

为了进一步说明三级可重排无阻塞CLOS网络的工作原理，以－个4×4的三级CLOS网络为例进行解释，如图2．26所示。假设n₂＝i₁＝o₃＝2，显然，不满足严格无阻塞条件。

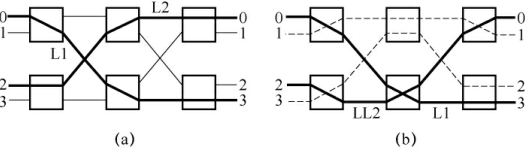
图2．26　m＝n＝r＝2可重排无阻塞的CLOS网络

参照图2．26（a）所示，假设在某一时刻要做如下交换连接，连接函数的排列表示式为：

假定先建立了入线0到出线3的连接，其路径为L1和入线2到出线0的连接，其路径为L2，现在要建立入线1到出线1的连接以及从入线3到出线2的连接，其请求会遇到内部阻塞。但是有可能重新调整已有的从入线2到出线0的连接，使其由路径L2变成路径LL2，这样就会发现调整后入线1到出线1以及入线3到出线2的连接就能建立了，如图2．26（b）中虚线所示。这样的网络称为可重排无阻塞的CLOS网络，它可对已有路径进行重排，使得有阻塞的三级CLOS网络成为无阻塞的网络。可见，对称三级CLOS网络可重排无阻塞条件可以写为：

其中，m为三级CLOS网络中间级所需要的交换单元的个数，n为三级CLOS网络第一级交换单元入线数和最后一级交换单元的出线数。