跨文化研究发现：计算在认知心理学中的重要性

跨文化认知研究中最引人注目的是围绕数学（通常是算术）知识和问题解决的研究。可以想象，算术系统的发展和运用对几乎所有文化中的众多种日常活动来说都是必不可少的：购物、售货、买卖、做账、确定相对数量等等。我们饶有兴趣地注意到，并不是所有的文化都发展出了同样的系统，因此对这些系统方式的形成进行审视是很有意义的。

让我们先来讨论有关计算的算术技巧问题。Rochel Gelman和Randy Gallistel（1978）研究了美国学龄前儿童，证明即便是很小的美国儿童也知道大量的计算知识。对于小数目（即，比5小的数），即使是2、3岁的孩子也能一下子数清。但是，计算意味着什么呢？Gelman和Gallistel给出了一个惊人复杂的定义：

［计算］包括几个部分的协调运用：依次地注意一批项，把每一个注意到的项与一个数字名称匹配；以常规的顺序运用数字名称的常规列表；认出所用到的最后一个名称代表了这批项的数值（p.73）。

Gelman和她的同事观察了学龄前儿童的计算行为，可以识别出计算的几条独特“原则”，如下所列：

1.一一对应原则：在有待计数的数组中，每一项皆以被赋予一个且是唯一的不同“记号”的方式来加以“标记”。

2.固定顺序原则：分配给每项的标记（数字名称）必须以一个固定顺序排列，并可重复。

3.基数原则：当一个人在计数一个数组时，最后一个标记代表了这组项目的数量。

4.抽象原则：任何群体的项目，有形的或无形的，同类的或不同类的，都可以计算。

5.次序无关原则：一组项目中计数的次序（即，哪项标“1”，哪项标“2”，等等）并不会影响到一组项目的数量或计数程序。

儿童可能具备其中一些原则，但无论在哪个发展阶段，儿童都不可能掌握所有这些原则。不过，即使她的“计数”行为和成人的不完全一样，当她的行为表明已经能够遵循至少其中部分原则时，就可以认为她是在“计数”。例如，一个2岁半的儿童这样计算一个盆子中的三只玩具鼠：“一、二、六！”当实验者要求他再数一遍时，这孩子高兴地照办了：“呀，一、二、六！”（Gelman & Gallistel，1978，p.91）该儿童表现出了清晰的证据证明她遵循了一对一原则和稳定次序原则，因而是真的在计算，即使所运用的是一种与成人不同的计算语言系统。

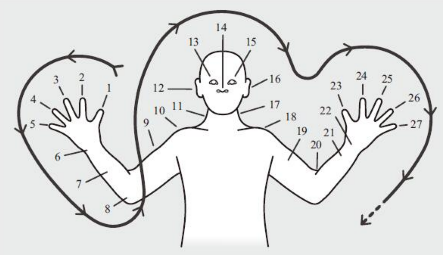
Geoffrey Saxe（1981；Saxe & Posner，1983）的跨文化研究发现则表明，不同文化中的计算系统也有所不同。Saxe报告了对巴布亚新几内亚的偏远村庄欧克萨平儿童所作的研究。与在我们文化中所使用的以10为基数的数字系统不同，Saxe发现欧克萨平人发展出了一种没有基数结构的身体-部位计数系统。欧克萨平人在手、臂、肩、颈和头部标记了27个不同的身体部位。就像我们用手指计数一样，欧克萨平人用手指，也用手臂、肩膀、脖子和头部各部位来计数，当他们要数一个比27大的数时，他们便会循环并添加前面的数字。图14-8说明了欧克萨平人的计数系统。

(www.xing528.com)

图14-8　欧克萨平计数系统。欧克萨平人使用的身体部位传统顺序依次为：（1）tip^na，（2）tipnarip，（3）bumrip，（4）h^tdip，（5）h^th^ta，（6）dopa，（7）besa，（8）kir，（9）tow^t，（10）kata，（11）gwer，（12）nata，（13）kina，（14）aruma，（15）tan-kina，（16）tan-nata，（17）tan-gwer，（18）tan-kata，（19）tan-tow^t，（20）tan-bir，（21）tan-besa，（22）tan-dopa，（23）tan-tip^na，（24）tan-tipnarip，（25）tan-bumrip，（26）tan-h^tdip，（27）tan-h^th^ta

有人对Saxe及同事提出了一个问题：欧克萨平人使用的“无基数”计数系统是否会改变对特定数目关系的理解。比方说，皮亚杰的数量守恒任务（若需要回顾，请见第12章）依赖于对“更多”或“更好”概念的理解，这种任务对欧克萨平儿童比对美国儿童更加难吗？Saxe（1981）发现，尽管欧克萨平儿童发展计算和守恒的概念普遍较晚，但他们的发展类型却和美国儿童颇为相似。有趣的是，新近采用的货币经济比传统的欧克萨平生活需要更多的算术计算，经常参与这一经济系统的欧克萨平人正在改变并且重新组织他们的身体-部位计数系统，以使计算更容易。

近期有一项研究涉及了计数系统及其与计算关系方面的问题。K. F. Miller、Smith、Zhu和Zhang（1995）要求来自伊利诺伊州厄巴纳-香槟市和中国北京的学龄前儿童完成多种形式的计算任务，然后加以比较。这一比较很有意思，因为汉语与英语的数目命名规则不同。两者都有从1到10不同的数字名称，且名称之间没有预测关系：即不能从8叫作八，预测9会叫作九；1到10的数字名称是没有次序的。

然而，对于数字中的第二组十个数字，两种语言就产生了分歧。汉语采用了一种以10为基数、连贯的指称系统：11汉语直接称为“十一”。但是英语里11和12的名称（eleven & twelve）并没表示清楚这两个数字与1和2的关系。在数字20以后，尽管英语比汉语多了一些花样（比如把20叫作twenty），这两种语言又开始用类似的方式来命名数字了。调查者预计，中国的学龄前儿童会比较容易学会计数，尤其是计算11到19的数字。

实验中给儿童各种各样的计算任务。如，要求儿童尽可能多地数数，一旦他们停下来就会得到实验者的提示，让他们继续数下去。儿童数到的最后一个数作为他的计数水平。图14-9显示了不同年龄的学龄前儿童计数水平的中位数。虽然两国的三岁儿童都能数到差不多大小的数，但是4岁和5岁的中国儿童比他们的美国同龄人可以数到更多。

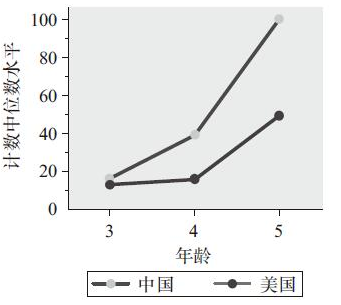
图14-9　不同年龄和语言条件下抽象计数（所能数到的最大数值）中值水平。在4岁和5岁组发现说汉语的儿童表现明显要好，但3岁组未见差异

研究者（K. F. Miller et al.，1995）还调查了中美儿童数数在什么地方停下来究竟有没有模式上的区别。只能数到10以下儿童的百分比没有差别：研究者发现94%的美国儿童和92%的中国儿童都能数到10。但是，只有48%的美国学龄前儿童能数到20，相比较而言，74%的中国学龄前儿童能数到20，这真是一个显著的差异。在接下去的几十个数字中，这个差异没有扩大。这表明，美国儿童的计数不如中国儿童的原因在于：两种语言中一个（中文）弄清了以10为基数的数字系统本身；而另一个语言系统没弄清，这就是差异所在。

K. F. Miller等人（1995）认为，这种源于语言系统的差别有助于解释为什么在计算方面中日学龄前儿童表现得比美国同龄人更出色。虽然相比一些亚洲国家，美国的算术教学已经被证实存在许多不足之处（Stevenson et al.，1990），但是Miller等人宣称，问题的一部分（至少是部分地）可以追溯到儿童入学时对以10为基数的数字系统理解的根本差异。

近期的关于数字认知的跨文化研究验证了来自不同文化的人们如何把数字映射到“心理数值线”（一种内部表征的方法，在这种方法中，不同的数值彼此相关，两个较近距离的数值描述了较近的数值关系）上。对于这种心理表征的特性是否具有文化相关性和普遍性的争论始终在进行（Bender，2011；Nuñez，2011）。

我们在这一部分回顾了一些认知任务在不同文化中不同表现的研究实例，也意识到学校教育是影响许多不同认知任务的一个重要变量。在下一部分中，我们将更加仔细地讨论这一变量所产生的效应，尝试分离出是学校教育的哪些方面造成了这样的效应。