想一想专栏11-8中的问题,并从两个可能的答案中挑选一个。回答之后,请评判一下自己的信心水平。如果你对答案没有确定的把握,请用0.5来表示你认为正确的概率是50∶50,(低于0.5的数值表示你认为错的可能性更大,这样你就要选择另一个答案。)1.00表示你100%确定自己的答案是正确的。0.5~1.00表示中间水平的信心,比率越高,信心越大。
专栏11-8 几个小问题
每个问题只有一个答案,请用0.5(只是猜测)~1.0(完全确定)范围之间的数值评定你对每个答案的信心。
1.哪份杂志在1978年时发行量更大?
a.《时代》
b.《读者文摘》
2.哪个城市的人口在1953年更多?
a.明尼苏达州,圣保罗
b.路易斯安那州,新奥尔良
3.谁是美国的第21任总统?
a.亚瑟
b.克利夫兰
4.哪一艘联军装甲舰击破了南部邦联的装甲舰Merrimack?(https://www.xing528.com)
a.Monitor
b.Andover
5.谁开创了护士职业?
a.南丁格尔
b.巴顿
该讨论的目的并不在于答案的准确性。(如果你一定要正确答案,那么依次是b,a,a,a,a。)这里在乎的是你的准确率和信心评定之间的关系。在好几项研究中(Lichtenstein,Fischhoff & Phillips,1982年),给被试一长串类似专栏11-8的问题,在他们回答所有问题并对信心加以评定之后,根据准确率和他们自己的信心评定构成一种函数关系。比如,实验者可以找到被试的信心评定为0.6的所有问题,并计算其回答正确的比例。
典型的发现如图11-7所示。这种根据信心来标定准确率的曲线称为标定曲线(calibration curve)。曲线越接近斜率为45度的线,信心和准确率之间就越相配。注意,斜率为45度的线说明信心和正确率完全是同步的,被试信心评定为0.6的所有问题,其回答的准确率也应该是60%。然而,这样的发现可谓少之又少。相反,如图11-7所示,典型的曲线是“弓形的”而背离了45度的斜率。
曲线斜率越接近45度,信心与准确度的“吻合”就越好。低于这根线的曲线偏离体现了过分自信(overconfidence),即信心高于实际的准确度。高于这根线的偏离表示了信心不足,这种现象很少发生。这里的一般思想是:如果所有被试给出0.8信心评定的问题(这意味着他们估计答案准确的可能性是80%),其实只答对了60%。而被试认为自己100%正确的答案,也只有75%~80%是对的。
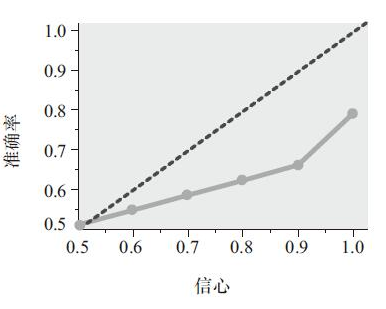
图11-7 一条标定曲线的例子
换种方式讲,人们对自己回答准确率的感觉是被夸大的。过分自信对正确的决策而言是真正的阻碍。如果你对自己判断的信心不恰当的高时,你可能会摒弃所有决策中提供的帮助,因为你看不出有此必要。即使可以帮助你克服其他偏见和判断失误的办法就在身边,过分自信会使你偏信自己的直觉,而不去相信可以获得的其他客观信息。过分自信其实就是决策中的自大。
到目前为止,我们已经回顾了(很不完整的)一系列在决策制定和计划中存在的启发式和偏见。再次重申的是,这些收集和评估信息的方法并不总是错的或不好的。相反,这些例子指出了决策不能如人所愿顺利进展的地方。这些偏见的存在同样告诉我们,人是怎样“自然”地处理信息的,尤其是在信息丰富的时候。记录这些错误可为我们设立有效的纠正方案迈出第一步。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




