格式塔心理学家韦特海默的例子揭示批判性思维

许多关于创造力的观点，是根据人们产生一些最初看来似乎“与众不同”或是“毫无联系”的想法的能力而提出的。然而，一旦一个新异的想法产生之后，就必须对它进行恰当与否的评价和判定。提出的解决方法是否确实满足所有的目标和限制呢？想法中是否有隐藏的细微瑕疵呢？主张的含义又是什么呢？

能够提出这些问题的人应该是在做心理学家、哲学家和教育学家称为的批判性思维（critical thinking）的工作。批判性思维的定义有许多，杜威（Dewey，1933）称之为“反省思维”，并将之定义为“根据其支持的背景以及倾向于做出的进一步结论，对任何观念或知识的可能形式进行积极、持久、仔细的考虑”（p.9）。杜威将反思与其他胡乱的想法、机械回忆以及信仰等人们无根无据的思考形式区分开来。

格式塔心理学家韦特海默（Wertheimer，1945）提出的几个例子很好地说明了批判性思维。其中有一个涉及学习如何求平行四边形的面积。一种教授的方法是给出公式，例如高中几何课本中为人熟悉的公式：面积＝底边×高。图10-13a展示了一个平行四边形的样例，并且标明了底边和高。

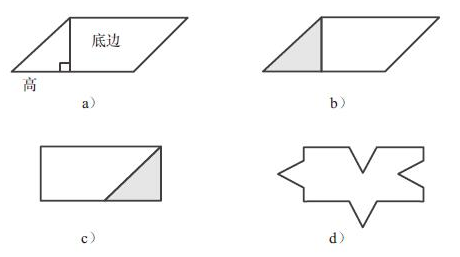
图10-13　平行四边形及其他几何图形

如果学生仔细记住了这个公式，他就会用一种死记的方法，也就是韦特海默所称的机械背诵的方法来解决这个问题。然而问题是，如果这个学生忘记了这个公式，他会完全不知所措。韦特海默认为，更好的方法是尽力教会学生抓住问题的“基本结构”，即确认并理解问题的基本内容。

考虑图10-13b中展示的另一个平行四边形。注意阴影区域，假设将这一部分从平行四边形上切除并填补到另一端，如图10-13c所示，这一变形会创造出一个熟悉简单的几何图形——矩形。求矩形的面积公式是众所周知的（底边×高）。注意，变形是将从左边切除的那块区域原封不动地填补到右边，因而，整个面积没有改变。取而代之的是，创造出了一个具有相同面积、更加“规则”的几何图形。(www.xing528.com)

教授这种解决方法的好处是什么？首先，它更加概括。这种方法不仅适用于平行四边形，同样也适用于许多不规则的几何图形，如图10-13d所描绘。其次，这个解决方法展现了对公式适用原因的更加深层次的理解。在这个实例中，公式并不是简单机械地运用于这个问题，而是产生于学生对平行四边形作为一个几何图形本质的理解。

在近来关于批判性思维的研究中，Perkins和他的同事们（Perkins，Allen & Hanfner，1983）呈现给不同学历水平的学生和成人不同的矛盾论题，要求被试对每个论题进行推理。一个例子是“需要对瓶子或罐头收取5美分的押金这一法律条款是否能够减少乱扔垃圾的情况”（Perkins et al.，p.178）。实验通过观察被试几次对自己思考提出的反对或挑战来测试他的批判性思维。其中一个较好的批判性思维的例证如下。

法律条款希望人们为了5美分归还瓶子而不是到处乱扔。但我认为如今人们并不在乎5美分。但是等一下，这不是一次性5美分，因为人们可以在地下室积存一箱一箱的瓶子或一袋一袋的罐头，然后一次性地将它们交回，所以也许他们会这么做。但是，也许并不是这些瓶子和罐头被到处乱扔，而是外出野餐的人或是街头和公园里的孩子乱扔瓶子和罐头。他们不会费心为了一个镍币而归还它们，但是另一些人也许会（p.178）。

请注意这里思维的结构：每一句都在某些方面对上一句提出反驳。

用Perkins的话来说，良好的思维需要庞大的知识库以及高效使用的方法。同时，良好的思维还需要如刚才所示的质疑。通常阻碍批判性思维的是一种心理懒惰，即一旦找到一个解答就停止思考。一个无批判力的思考者对瓶子议案做如下推理：“嗯，尝试减少垃圾是很好的，但是5美分不足以让人们这么做，所以行不通。”注意在这个例子中，此人只建立了一种心理情景就停止了，没有提出任何假设问题或是思考任何其他可能性。Perkins等人（1983）敦促人们克服这种只有当问题完全表面化之后才对它们进行推理的倾向，而换以更加努力、持久地搜寻其他的可能和解释。