问题空间假说：解决问题的关键路径

研究问题解决的学者通常以在心理上搜寻一个问题空间来思考问题解决的过程（Baron，2008；Lesgold，1988；Newell，1980；Newell & Simon，1972）。问题空间假说（problem space hypothesis）的主要观点是，问题中事态进行的每一种可能状态对应于心理曲线图上的每一个节点。所有节点的分布占据一些心理区域，这个区域连同曲线就是问题空间。

图10-9展示了一般问题空间的示意图。每一个圆圈或是节点，对应于问题解决过程中某一时刻事态进行的某一状态。例如，如果问题是赢得象棋比赛的胜利，那么每一个节点对应于比赛中每一时刻可能形成的局面。标记为“初始状态”的节点对应于问题的初始情况，比如，第一步落子之前的棋盘格局。目标状态对应于问题解决后的状态，例如，游戏获胜时的棋局。中间状态（未在这一示意图中标记）由其他节点表示。

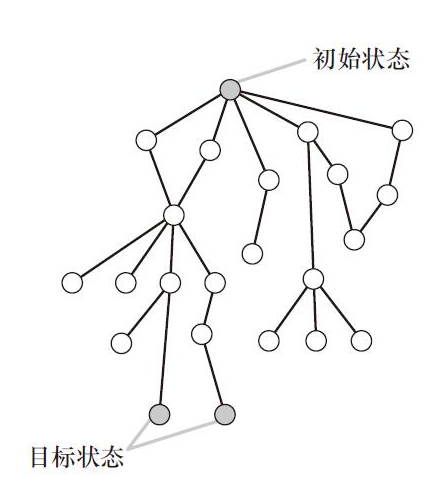
图10-9　一般的问题空间

如果可能通过某些操作从一个状态移至另一个状态，这步移动可以通过连接两个节点的直线在问题空间中加以表示。任何“心理移动”的次序都可以用从一个节点向另一个节点移动次序来加以表示。任何起始于初始状态、结束于目标状态的移动次序构成了通过问题空间的路径。图10-10描述的是一般的解决路径；图10-11描述了河内塔问题的部分问题空间。

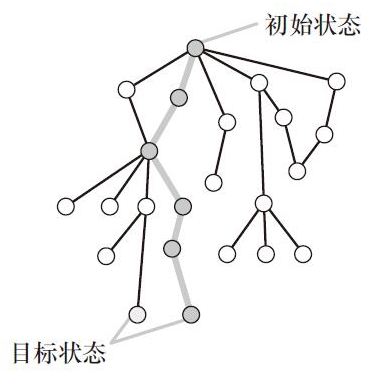
图10-10　通过问题空间的一条解决路径

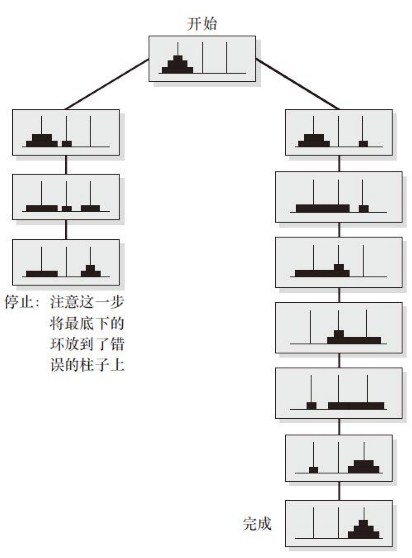
图10-11　部分河内塔任务的问题空间，显示了解决的方案

好的问题解决就是有效路径的建立：即尽可能简短，并且在初始状态和目标状态之间尽可能少地绕道。一般认为，最佳路径是通过搜索获得的，彻底的搜索往往可能产生答案。(www.xing528.com)

人工智能领域的研究者设计了不同的搜索算法以搜索问题空间（Nilsson，1998；Winston，1992）。其中之一是“深度优先”（depth-first）原则，即在返回检验其他可能选项之前，沿着曲线图尽可能深入地探索目标状态；另一个是“广度优先”（breadth-first）原则，即在更深地挖掘曲线走向之前，在已知水平下考虑所有的节点。不同的算法有不同的成功概率，当然这取决于曲线本身的性质。

Burns和Vollmeyer（2002）的一项研究有一些出乎意料的发现与搜索问题空间产生解决方法有关。他们相信探索问题空间会产生更佳的表现，而且他们认为，进程没有因为急于达到一个特定的目标而被缩短时，探索更可能产生。

Burns和Vollmeyer（2002）使用了如图10-12所描述的任务。让被试想象他们在实验室工作，并试图发现如何通过控制不同的成分输入以达到某种特定水质的效果。在这项任务中，他们可以通过改变输入成分（盐、碳、石灰）然后观察会产生什么样的输出结果（氧化作用、氯的浓度、温度）。事实上，图中显示输入具有线性关系，例如，盐量输入的改变会导致氯浓度6倍的增长。但是被试未被告知输入和输出的关系是什么（也就是，他们不会看到图中箭头上的数值）。

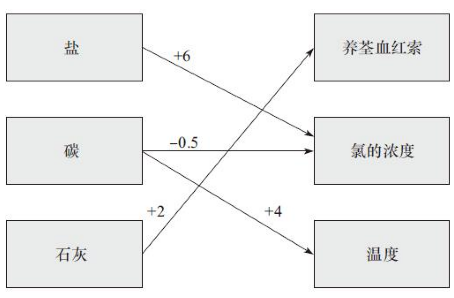
图10-12　水箱系统（注意氯的浓度指的是输出的氯的浓度）

所有的被试都被告知将最终要求他们依据特定的输出值来达到一定的目标。其中一些被试（称为“具体目标”被试）在任务一开始就给予他们特定的目标，但告知可以在一段探索阶段后再达成目标；另一些被试（称为“非具体目标”被试）直到经过搜索阶段后才告知他们目标是什么。在探索阶段之后，给所有被试一张类似于图10-12的示意图，但没有显示任何联系，要求被试在输入、输出之间画出连接线，如果他们认为自己确实知道的话，在连接线上标出方向和权重。研究者从中获得一个“结构分数”来计算被试关于联系方向与权重正确值的知识程度。

“非具体目标”被试比“具体目标”被试获得更高的结构分数。当要求输出达到特定目标值时，两组的表现相当，但在一个有新目标值的迁移问题上，“非具体目标”被试的表现要优于“具体目标”被试。Burns和Vollmeyer（2002）做了一个追踪研究，要求其中两种情况下的被试完成任务时出声报告想法。结果显示，非特定目标被试在搜索阶段更易于检验特定的假设。由此推测，以Newell和Simon的术语来说，尽管不同的任务都会产生不同的成本，拥有一个特定目标会减少致力于搜索问题空间的努力。

问题空间假说同样也可以帮助我们理解问题解决的障碍是如何发生的。未能对空间的某些部分进行搜索（例如，由于心理定势）会阻碍问题的解决。当解决方法位于空间内一个未能搜寻到的部分时，不完整或不正确的表征可能造成建构一个不完整或不正确的问题空间，反过来也不利于问题解决。

专长的获得是另一种搜索问题空间的方式，也许专长会令人们发展出更好的预感，即对问题空间的哪些区域进行搜索是最有效的，应该以怎样的顺序去搜寻可能得到结果。