问题解决中一个相关的困难与最初对问题的解释有关。如果问题被误解了,或是关注了错误的信息,问题解决者无疑将处于不利的境地。“棋盘问题”说明了这种现象对问题解决的阻碍。
如图10-7所示,有一个斜对角两个方块被切除的标准国际象棋棋盘。棋盘旁边是一些多米诺骨牌,每一张牌恰好占据棋盘的两格。完整的棋盘有64个方格,你应该很清楚这点。所以图中的棋盘还有62格。有没有一种摆放方法可使31张多米诺骨牌完全覆盖这个棋盘呢?
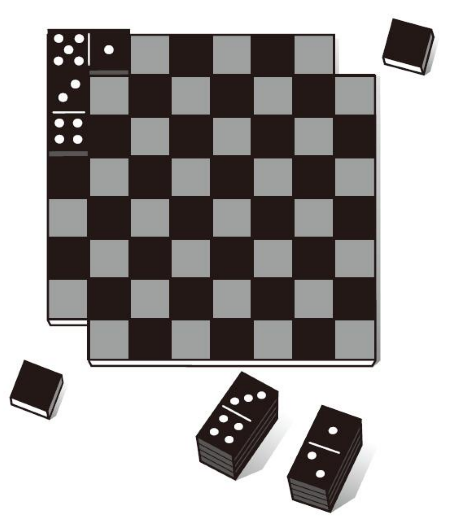
图10-7 残缺棋盘问题
31张多米诺骨牌能够覆盖满剩余的棋盘吗?每张骨牌正好覆盖两个格子
解决的关键是意识到无论怎样摆放,根据棋盘的格式,每一张多米诺骨牌将覆盖一块黑格和一块白格。但是现在请注意,那两块切除的方格是同一颜色的。由于一张骨牌必然覆盖两块不同颜色的方格,因此不可能将31张骨牌覆盖满残缺棋盘的所有方格。
大多数人解决这个问题的困难之处在于他们没能在关于问题的最初表征中包含这两条至关重要的信息,因而造成了表征的不完整。同样,在前述的棒球赛问题中(男人在home),用“一个人待在房子里”表征这个问题会使你误入歧途。这就是使用错误表征的范例,包含了问题中既没有呈现也不是正确的信息。(https://www.xing528.com)
对表征的选择往往会造成很大的差异。研究专栏10-2中“女士、狗、子女、职业问题”的S. H. Schwartz(1971)发现,建构图10-3中图表的人比那些仅仅写下名字、狗、职业之类并且以箭头或连线连接他们的人(例如,凯茜——爱尔兰长毛猎犬;金毛猎狗——4个孩子)在解决问题时更为成功。
这里还有一个很著名的例子,它展示了表征的形式会使一个问题要么变得很简单,要么很复杂,它被称为“数字游戏”。每个游戏者的目标是从数列中抽取三个数字,并使数字之和为15。呈现给两个玩家的数字为1,2,3,4,5,6,7,8,9,他们轮流从中选取一个数字并加入自己的数列之中,谁第一个使数字之和为15(例如4,5,6或是1,6,8)谁就获胜。
如果让你玩这个游戏,你会采用什么样的策略?如果让你先选,你会选择哪个数字?如果你后选,而且对手已经选择了5呢?第一次、第二次玩的时候,你也许会发现很具挑战性。现在来看图10-8,它展示了另一种表征这个问题的方法。注意,以这种方式来描述的话,困难的“数字游戏”实际上是变形的“井字游戏”(tic-tac-toe)。如图10-8所示,游戏很简单,但是没用这种表征,问题解决起来就要难得多。
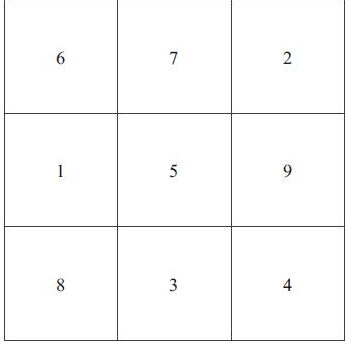
图10-8 用“井字游戏”方块来表征数字游戏
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




