太阳能光伏技术：太阳电池I-V特性测试原理

在光照条件下太阳电池等效电路模型如图14．3所示。

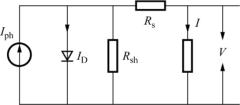
图14．3　太阳电池等效电路图

电压电流特性可以由下式给出：

式中：I，V分别是电池的输出电流和输出电压，Iph是光生电流，q是电子电量，Io是反

向饱和电流，kB是玻耳兹曼常量，T是绝对温度，n是二极管理想因子（在1～2之间），Rs是串联电阻，Rsh是并联电阻。

基于式（14－4），文献［5］从理论上分析串联电阻对各参数的影响，式（14－4）表明I是V的超越隐函数，我们采用Lambert’s W函数［6］来改写式（14－4）。

Lambert’s W函数是方程：的解。可以借助数学软件Matlab的Lambert’s W函数对其求解。

基于Lambert’s W函数，我们将方程（14－4）显化［7］为

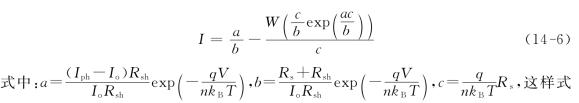(www.xing528.com)

（14－6）表达I是V的显函数，给定一个V值，就容易由计算机求出I值。

对于一个典型的商业丝网印刷125mm×125mm的单晶太阳电池来说，我们取n＝1．32，Rsh＝300Ω，Io＝4．0×10－8 A，kB＝1．38×10－23 J／K，q＝1．6×10－19 C，T＝298K，一个太阳下的光电流Iph＝5．25A。

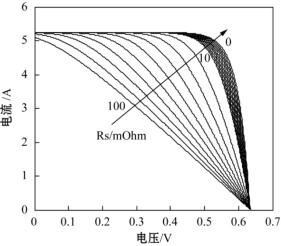
图14．4　不同串联电阻下的I－V特性曲线图

根据上述条件下，取串联电阻Rs的阻值可变：Rs在0～10mΩ内时，每1mΩ取一个值，Rs在0～100mΩ内时，每10mΩ取一个值。按照式（14－6）通过Matlab编程，我们计算了每一Rs下的电压电流I－V样本点，并由通过各样本点作图，如图14．4所示。

从得到的I－V样本点求得不同串联电阻Rs下太阳电池六个特性参数：短路电流Isc，开路电压Voc，最大功率Pm，最大功率点电流Im，最大功率点电压Vm以及填充因子FF。串联电阻与各参数关系如图14．5（a），（b）所示。

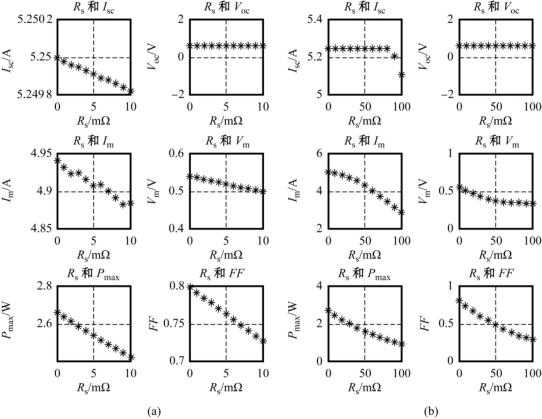
图14．5　不同预设值下Rs与各参数关系图（a）Rs属于（0～10mΩ）　（b）Rs属于（0～100mΩ）

对于图14．5（a），即Rs较小，处于0～10mΩ区间，当串联电阻增大时：开路电压基本不变；短路电流、最大功率点电流有小范围的降低；但是，最大功率、最大功率点电压、填充因子明显降低，而且这种降低具有线性的关系。对于图14．5（b），即Rs较大，处于0～100mΩ区间，当串联电阻增大时：开路电压基本不变；短路电流在Rs＝70mΩ处出现拐点后迅速下降；最大功率点电流从串联电阻Rs很小时的微弱降低变为明显下降；最大功率、最大功率点电压、填充因子大大降低，但这种降低从最初的线性下降减弱为负指数降低，这与文献［8］中所提到的结果一致。

串联电阻的大小和电池性能的表现参数的关系如此相关，串联电阻的增大使电池效率急剧降低，因此，串联电阻的准确测试对电池性能的分析，工艺流程的优化至关重要。